§ 8. Подобные матрицы и их спектральные задачи
Две квадратные (nn) матрицы A, B M(n, F) называются подобными или сопряжёнными, если существует обратимая матрица T GL(n, F), называемая сопрягающей матрицей для A и B, со свойством T –1AT = B.
Примеры:
1. Матрицы
A
=
, B
=
M(2,
F)
сопряжены
с помощью сопрягающей матрицы T
=
:
T
–1AT
=
=B.
2.
Матрицы A
=
и B
=
M(2,
F)
не подобны.
Действительно, если бы существовала сопрягающая матрица T GL(2, F), то B = T –1AT и 1 = |B| = |T –1||A||T| = |T |–1|A||T| = |A| = 0 – противоречие.
3.
Матрицы A
=
и B
=
M(2, R)
не сопряжены при любом
1 и сопряжены
при
= 1.
Действительно,
если существует невырожденная
сопрягающая матрица T
=
GL(2, R),
то B = T
–1AT
, т.е. TB
= AT
или
.
Таким
образом, получается система линейных
уравнений
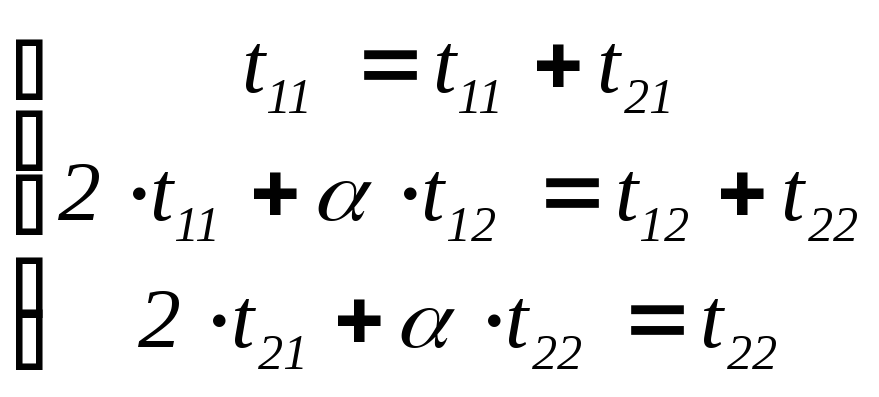, откудаt21
= 0, (
– 1)t22
= 0, 2t11
= t22
–(
– 1)t12
. Если
= 1, то
сопрягающей матрицей будет T
=
при t11
0.
Если же 1, то t21 = 0 = t22 и матрица T вырождена, что невозможно.
Теорема (о спектральных задачах подобных матриц). Пусть матрицы A, B M(n, F) подобны, т.е. B = T –1AT для некоторой обратимой матрицы T GL(n, F). Тогда
Sp(A) = Sp(B),
вектор v n F \ {0} является собственным вектором матрицы А, отвечающим собственному значению Sp(A), тогда и только тогда, когда вектор T –1v n F \ {0} является собственным вектором матрицы B, отвечающим собственному значению Sp(B).
Доказательство следует из цепочки Av = v TBT –1v = v (BT –1)v = (T –1v) с учётом того, что v 0 T –1v 0 .
Теорема доказана.
§ 9. Post Scriptum : о подобии матриц
Укажем некоторые важные случаи, когда матрицу можно путём сопряжения с помощью невырожденной матрицы привести к более простому виду.
I.
Диагонализируемые матрицы.
Матрица A
M(n,
F)
называется
диагонализируемой,
если она подобна некоторой диагональной
матрице. Другими словами, – если
существует обратимая матрица T
GL(n,
F)
со свойством
T
–1AT
=
–диагональная
матрица. Если существует базис векторного
пространства V,
в котором матрица []e
имеет
диагональный вид, то линейный оператор
: V
V
называется диагонализируемым.
Теорема (о диагонализируемости). (1) Матрица A M(n, F) диагонализируема тогда и только тогда, когда пространство n F имеет базис, состоящий из собственных векторов матрицы A .
(2) Линейный оператор : V V диагонализируем тогда и только тогда, когда пространство V имеет базис, состоящий из собственных векторов оператора .
Доказательство.
(1)
Если T
–1AT
=
–диагональная
матрица, то di
очевидно
будет собственным числом диагональной
матрицы, а eit
– её
собственным вектором, отвечающим di
(1
i
n). Тогда
T(e1t
, … , ent)
– базис
пространства n
F,
состоящий из собственных векторов
матрицы A
(см. теорему о спектральных задачах
подобных матриц).
Обратно,
пусть v
= (v1
, … , vn)
– базис
пространства n
F,
состоящий из собственных векторов
матрицы A,
а
: n F
n F
– линейный оператор, заданный правилом
x
n F
(x)
= Ax.
Тогда для стандартного базиса e
= (e1t
, … , ent)
имеем []e
= A и
[]v
= Te,v–1ATe,v
, где Te,v
– матрица
перехода от базиса e
к базису v.
Кроме того, (vi)
= Avi
= ivi
для
соответствующего собственного значения
i
F, так что
[(vi)]v
= iei
(1
i
n)
и Te,v–1АTe,v
= []v
=
– диагональная
матрица.
(2) следует из определения диагонализируемости линейного оператора и связи спектральных задач линейного оператора и его матрицы.
Теорема доказана.
Примеры:
1. Матрица
A
=
M(2,
R)
не
диагонализируема, т.к. не имеет в R
собственных
чисел.
2.
Матрица A
=
M(2,
С)
диагонализируема,
т.к. Sp(A)
= {i,
–i}
и C
2
имеет
базис (
),
состоящий из соответствующих собственных
векторов.
3.
Матрица A
=
M(2, F) не
диагонализируема над любым полем F
: у ней
единственное собственное число
= 1, а
отвечающие ему собственные векторы
имеют вид
,
F
\ {0} и не
образуют базиса в 2
F.
4.
Матрица A
=
M(2, R)
диагонализируема
над R
: Sp(A)
= {1, 2} и (
)
–
соответствующий базис из собственных
векторов.
Теорема (достаточное условие диагонализируемости). Линейный оператор в n-мерном векторном пространстве с n различными собственными значениями диагонализируем.
Доказательство. Пусть 1 , … , n – различные собственные числа линейного оператора : V V в n-мерном векторном пространстве. По каждому из них найдём собственные векторы v1 , … , vn V \ {0} и докажем их линейную независимость.
Если 1v1 + … + nvn = 0 – нетривиальная линейная комбинация, то, подействовав оператором , получим
0 = (1v1 + … + nvn) = 1(v1) + … + n(vn) = 11v1 + … + nnvn ,
т.е. 11v1 + … + nnvn = 0. Вычитая из этого равенства исходное соотношение линейной зависимости, умноженное на 1 , получим новое соотношение 2(2 – 1)v2 + … + n(n – 1)vn = 0. Оно не может быть тривиальным, т.к. в случае 2 = … = n = 0 получаем 1v1 = 0, т.е. v1 = 0, что невозможно.
Продолжая процесс исключения векторов v2 , … , vn–1 , придём к невозможному нетривиальному соотношению nvn = 0. Полученное противоречие показывает, что векторы v1 , … , vn V линейно независимы, а их количество равно n = dim V. Значит, они образуют базис векторного пространства V.
Теорема доказана.
II. Нильпотентные матрицы. Матрица A M(n, F) называется нильпотентной, если A k = 0 nn для некоторого k N. Аналогично, линейный оператор : V V в векторном пространстве V называется нильпотентным, если k = 0 – нулевой оператор для некоторого k N. При этом число k называется индексом нильпотентности матрицы и линейного оператора соответственно.
Примеры:
матрицы (0)
M(1,
F),
M(2,
F),
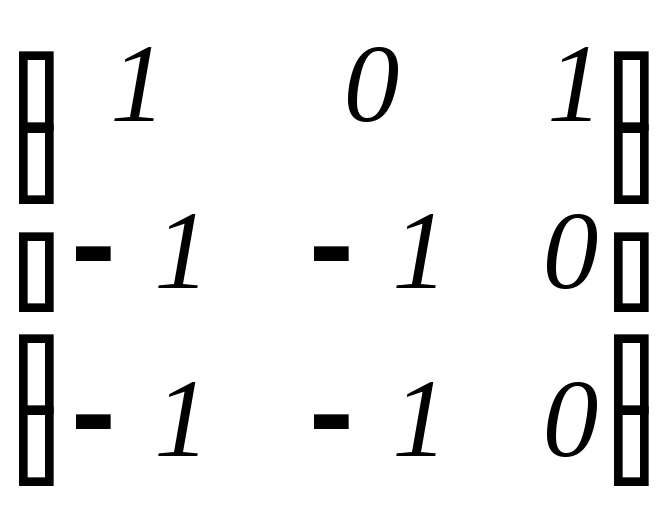
M(3,
F)
нильпотентны
с индексами нильпотентности 1,
2, 2, 3 соответственно,
в чём нетрудно убедиться непосредственным
вычислением степеней матриц.
Матрица A M(n, F) называется строго верхнетреугольной, если все её компоненты, стоящие как на главной диагонали, так и под ней нулевые. Аналогично определяется понятие строго нижнетреугольной матрицы.
Примеры: 1. среди матриц предыдущего примера строго верхнетреугольными будут первая и третья.
2.
матрица
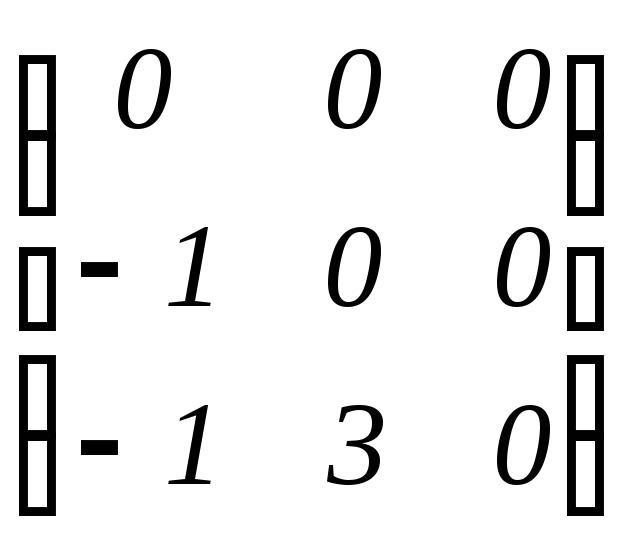строго нижнетреугольна, а матрица
таковой не является.
Теорема (о нильпотентных матрицах и линейных операторах). Следующие условия для матрицы A M(n, F) (соответственно для линейного оператора : V V) эквивалентны:
матрица A (или линейный оператор ) нильпотентна (нильпотентен),
Sp(A) = {0} (или Sp() = {0}),
А подобна строго верхнетреугольной матрице (или матрица []e строго верхнетреугольна в некотором базисе e векторного пространства V),
А подобна строго нижнетреугольной матрице (или матрица []e строго нижнетреугольна в некотором базисе e векторного пространства V).
Доказательство. Будем доказывать только утверждения для линейного оператора, т.к. матрица A M(n, F) нильпотентна тогда и только тогда, когда нильпотентен линейный оператор : V V , заданный правилом x n F (x) = Ax .
(1) (2) Если = 0, то доказывать нечего. Будем считать, что k = 0, но k–1 0. Тогда x V (v = k–1(x) 0) ((v) = k(x) = 0 = 0v) , т.е. v – собственный вектор , отвечающий собственному числу = 0.
Если предположить вопреки доказываемому, что 0 Sp(), то рассматривая соответствующий собственный вектор w, получим
(w) = w, 2(w) = ((w)) = (w) = (w) = 2w,
3(w) = 3w, … , k–1(w) = k–1w, 0 = k(w) = kw ,
что противоречит предположению 0 и условию w 0. Значит Sp() = {0}.
(2) (3) Рассмотрим -инвариантное подпространство U = Im() векторного пространства V. Если U = {0}, то v V (v) = 0 , т.е. = 0 и в любом базисе e пространства V матрица []e будет нулевой, а значит, строго верхнетреугольной.
Значит можно считать U {0}. При этом U V, т.к. в противном случае – эпиморфизм, и по теореме о сумме ранга и дефекта линейного оператора, выполнялось бы равенство
dim V = dim(Ker()) + dim U = dim(Ker()) + dim V,
из которого следует, что dim Ker() = 0, вопреки условию 0 Sp(): (v) = = 0v = 0 для собственного вектора v V \ {0}.
Итак,
U
– собственное
-инвариантное
подпространство. Если взять базис U
–
систему
векторов e
= (e1
, … , ek),
то дополнив его до базиса всего
пространства V
векторами e
= (ek+1
, … … , en),
получим базис e,
в котором матрица оператора
полураспавшаяся:
[]e
=
.
При этом имеем (ek+j)
Im()
= L(e1
, … , ek)
= U
(1
j
n–k),
т.е. B
= 0.
Рассмотрим линейный оператор h: U U, заданный правилом u U h(u) = (u) U и имеющий в базисе e матрицу A. Поскольку dim U < dim V, то можно считать (по индукции), что для оператора h утверждение (3) уже доказано, т.е. матрица [h]u является строго верхнетреугольной в некотором базисе u пространства U. Пусть T – матрица перехода от базиса (e1 , … , ek) пространства U к базису u . Тогда матрица [h]u = T –1AT = T –1[h]e T является строго верхнетреугольной и верхнетреугольна матрица
.
Теперь,
в качестве искомого базиса можно взять
(e,
e)
= (u,
e).
(3) (4) Если e = (e1 , … , en) – базис, в котором линейный оператор : V V имеет строго верхнетреугольную матрицу, то в базисе (en , … , e1) его матрица строго нижнетреугольна (?!).
(4)
(1) Пусть
линейный оператор
: V
V
имеет
строго нижнетреугольную матрицу A
=
в некотором
базисе e
= (e1
, … , en).
Достаточно доказать, что A
n
= 0: если это
так, то [
n]e
= []en
= A
n
= 0 и
n
= 0,
т.е. линейный оператор
нильпотентен
с индексом нильпотентности не выше n.
Докажем индукцией по m N, что матрица A m является строго нижнетреугольной и имеет m – 1 нулевую диагональ ниже главной. База индукции при m = 1 очевидна. Предположим, что
A
m
=
и докажем,
что в матрице A
m+1
= AA
m
будет нулевой
(m+1)-я
диагональ. По правилу вычисления
произведения
AA
m
матриц, (m+1+s,
s+1)-я
его компонента (т.е. s-й
элемент (m+1)-й
диагонали) вычисляется по правилу
(am+1+s 1 , … , am+1+s m+s , 0, … , 0)(0, … , 0, bm+1+s s+1 , … , bn s+1) t = 0
(0 s n–m–1). Легко видеть также, что нули и в предыдущих m диагоналях “не испортятся”. Значит, в матрице A n будет n нулевых диагоналей, что эквивалентно равенству A n = 0.
Теорема доказана.
Следствие (об индексе нильпотентности). Индекс любого нильпотентного линейного оператора в n-мерном векторном пространстве не превосходит n.
Доказательство. Если : V V нильпотентен, то в некотором базисе его матрица строго нижнетреугольна и n-я её степень равна нулю, т.е. n = 0.
Следствие доказано.
III. Идемпотентные матрицы. Матрица A M(n, F) называется идемпотентной, если A 2 = A . Линейный оператор : V V называется идемпотентным, если 2 = .
Примеры:
Матрицы 0,
In
M(n,
F),
M(2,
F)
идемпотентны,
в чём нетрудно убедиться непосредственным
вычислением.
Теорема (об идемпотентных матрицах и линейных операторах). Следующие условия для матрицы A M(n, F) (или для линейного оператора : V V) эквивалентны:
матрица A (или линейный оператор ) идемпотентна (идемпотентен),
А подобна матрице вида
,
где 0
r
n
(или матрица []e
в некотором базисе e
векторного
пространства V
имеет
указанный вид).
При этом для идемпотентной матрицы A (или оператора ) справедливы утверждения Sp(A) {0, 1} (или Sp() {0, 1}).
Доказательство. Как и в предыдущей теореме, докажем только утверждения для линейного оператора, т.к. матрица A M(n, F) идемпотентна тогда и только тогда, когда идемпотентен линейный оператор : V V , заданный правилом x n F (x) = Ax .
(1) (2) Докажем, что для идемпотентного оператора верны следующие равенства: Im() Ker() = {0} и V = Im() + Ker(). Последнее равенство следует понимать так: v V x Im(), y Ker() v = x + y.
Действительно, если u Im() Ker(), то v V u = (v) (u) = 0, так что 0 = (u) = 2(v) = (v) = u, что и требовалось. Кроме того, имеем v V v = (v) + (v – (v)), где (v) Im(), v – (v) Ker(), т.к. (v – (v)) = (v) – ((v)) = (v) – 2(v) = (v) – (v) =0.
Итак, Im() Ker() ={0} и V = Im() + Ker(). Если Im() = V, то Ker() = {0}, и оператор является изоморфизмом. В частности, в этом случае –1: V V –1 = idV = –1 и из идемпотентности 2 = получаем (умножая на –1) равенство = idV . Значит, в случае Im() = V матрица оператора в любом базисе равна In , где n = dim V.
Поэтому
можно считать, что dim(Im())
< n
. Зафиксируемем в Im()
базис u
= (u1
, … , ur)
и базис k
= (kr+1
, … , kn)
в Ker().
Тогда система векторов e
= (u1
, … , ur
, kr+1
, … , kn)
будет базисом
всего пространства V
и матрица оператора в этом базисе имеет
вид []e
=
(?!). Рассмотрим
оператор h:
Im()
Im(),
заданный правилом
x
Im()
h(x)
= (x)
с матрицей A
и заметим,
что Ker(h)
= {0}.
В самом деле, если x
= (v)
Im()
и h(x)
= 0,
то 0
= h(x)
= (x)
= ((v))
=
2(v)
= (v)
= x,
что и требовалось. Таким образом, h
– мономорфизм,
а значит и изоморфизм, т.е. по доказанному
выше h
= idIm()
и А = [h]u
= Ir
, что и
требовалось доказать.
(2)
(1) Если []e
=
,
то [
2]e
= []e2
=
= = []e
, т.е.
2 = .
Докажем теперь, что для идемпотентного оператора выполнено условие Sp() {0, 1}. Если = 0, то Sp() = {0} и доказывать нечего. Пусть поэтому x V v = (x) 0. Тогда (v) = ((x)) = 2(x) = (x) = v, т.е. v – собственный вектор оператора , отвечающий собственному значению 1. Таким образом, 1 Sp(). С другой стороны, если предположить, что Sp() \ {0, 1}, то (w) = w для некоторого ненулевого вектора w V, причём (w) = (w) = ((w)) = 2(w) = (w), ( – 1)(w) = 0, что невозможно, т.к. 1 и (w) = w 0. Значит Sp() {0, 1}.
Теорема доказана.
Замечание. Условие Sp() {0, 1} не равносильно идемпотентности оператора, т.к. иначе идемпотентными были бы все нильпотентные операторы. На самом деле одновременно идемпотентен и нильпотентен только нулевой оператор (?!)