
- •Министерство образования и науки Российской Федерации
- •Глава III. Евклидовы пространства
- •§ 1. Определения, примеры и простейшие свойства
- •Свойства скалярного произведения
- •§ 2. Длины и углы в евклидовых пространствах
- •Свойства длины в евклидовых пространствах
- •§ 3. Ортогональные базисы евклидовых пространств
- •§ 4. Изоморфизм евклидовых пространств
- •Глава IV. Теория линейных операторов в векторных пространствах
- •§ 1. Определение и простейшие свойства
- •Простейшие свойства линейных операторов
- •§ 2. Матричный формализм в векторных пространствах
- •Простейшие свойства матричного формализма
- •§ 3. Матрица перехода от базиса к базису
- •Свойства матрицы перехода
- •Изменение координатного столбца при переходе от базиса к базису
- •§ 4. Матрица линейного оператора
- •Координатная форма записи линейного оператора
- •Изменение матрицы линейного оператора при переходе от базиса к базису
- •Свойства матрицы линейного оператора
- •§ 5. Образ, ядро, ранг и дефект линейного оператора
- •§ 6. Инвариантные подпространства линейного оператора
- •§ 7. Собственные числа и собственные векторы линейного оператора
- •§ 8. Подобные матрицы и их спектральные задачи
- •§ 9. Post Scriptum : о подобии матриц
- •§ 10. Спектр симметричного оператора Ортогональные дополнения подпространств евклидова пространства
- •Симметричные линейные операторы
- •Глава V. Дифференцирования в банаховых пространствах
- •§ 1. Метрические пространства
- •Матричные нормы
Симметричные линейные операторы
Квадратная матрица
A
порядка n
над полем
F называется
симметричной,
если At
= A. Линейный
оператор h:
Fn
![]() Fn
называется
симметричным,
если его матрица в
стандартном базисе
симметрична. Нашей целью является
доказательство следующей важной теоремы:
Fn
называется
симметричным,
если его матрица в
стандартном базисе
симметрична. Нашей целью является
доказательство следующей важной теоремы:
Теорема (о спектре
симметричного линейного оператора).
Собственные
числа симметричного оператора h: Rn
![]() Rn
вещественны,
а его матрица диагонализируема (по
диагонали стоят собственные числа).
Rn
вещественны,
а его матрица диагонализируема (по
диагонали стоят собственные числа).
Доказательство.
Пусть A
– матрица
симметричного оператора h
в стандартном базисе,
=
+ i
– её
(возможно, комплексное) собственное
значение (,
![]() R),
а z
–
соответствующий
ему собственный вектор с (возможно,
комплексными) компонентами zk
= xk
+ iyk
(xk
, yk
R,
1
k
n). Тогда z
= x+
iy,
где x,
y
–
вещественные
векторы с компонентами xk
, yk
R,
(1
k
n). Задумайтесь:
почему у матрицы A
есть хотя
бы одно собственное число и собственный
вектор ?
R),
а z
–
соответствующий
ему собственный вектор с (возможно,
комплексными) компонентами zk
= xk
+ iyk
(xk
, yk
R,
1
k
n). Тогда z
= x+
iy,
где x,
y
–
вещественные
векторы с компонентами xk
, yk
R,
(1
k
n). Задумайтесь:
почему у матрицы A
есть хотя
бы одно собственное число и собственный
вектор ?
Так
как
Az
= z
,
то
A(x+
iy)
= (+
i)(x+
iy).
Учитывая,
что A
вещественная
матрица, и сравнивая действительные и
мнимые части в полученном равенстве,
приходим к двум условиям: Ax
= x
– y,
Ay
= y
+ x
. При
этом
(Ay
= y
+x)
((Ay)t
= (y
+
x)t)
(ytAt
= (yt
+ xt)).
Учитывая,
что At
= A,
получаем
систему
![]() . Умножая первое уравнение наyt
слева, а
второе – на x
справа, и
вычитая одно из другого, приходим к
равенству
. Умножая первое уравнение наyt
слева, а
второе – на x
справа, и
вычитая одно из другого, приходим к
равенству
0 = –yty – xtx = –(y12 + … + yn2 + x12 + … + xn2).
Отсюда либо
= 0, либо y1
= … = yn
= x1
= … = xn
= 0. Последняя
возможность исключается, т.к. собственный
вектор z
= x+
iy
ненулевой,
и, значит,
= 0. Итак,
![]()
R
.
R
.
Для доказательства диагонализируемости матрицы A проведем индукцию по n и докажем, что существует такая ортогональная матрица S, что матрица S –1AS = D диагональна с собственными числами матрицы A по диагонали (ортогональность матрицы S означает, что S –1 = S t – транспонированная матрица). При этом будем рассматривать пространство nR как евклидово со стандартным скалярным произведением (x, y) = xty .
База индукции (n = 1) очевидна. Предположим, что любая симметричная матрица порядка n – 1 диагонализируема с собственными числами по диагонали, и докажем это для матрицы A порядка n. Пусть – одно из её собственных чисел (которые, по доказанному выше, все вещественны), а x – соответствующий собственный вектор с вещественными (?!) компонентами и U = L(x) – одномерное подпространство в nR , натянутое на вектор x. По теореме об ортогональном дополненииподпространства имеем nR = U U, где U = { y nR | xty = 0 }.
Заметим, что
y
U
Ay
U.
Действительно,
xtAy
= (?!) = (Ax)ty
= = (x)ty
= xty
= 0. Таким
образом, если f1
, … , fn–1
– ортонормированный базис пространства
U
, то Afi
=
![]() .
Это значит,
что в базисе e
= (x,
f1
, … ,
fn–1)
матрица
[h]e
распавшаяся:
.
Это значит,
что в базисе e
= (x,
f1
, … ,
fn–1)
матрица
[h]e
распавшаяся:
[h]e
= T
–1AT
=
![]() ,
,
где
B
= (bij)
M(n–1, F),
T
= (![]() ,f1
, … , fn
),
T
–1
= T
t
.
При
этом
полученная
матрица
снова
симметрична:
,f1
, … , fn
),
T
–1
= T
t
.
При
этом
полученная
матрица
снова
симметрична:
(T –1AT)t = (T tAT)t = T tA t(T t)t = T tAT = T –1AT.
В частности, симметрична матрица B, к которой применимо предположение индукции.
По предположению индукции, B = P –1P, где P –1 = P t , – диагональная матрица с собственными числами матрицы B по диагонали, так что
![]()
– диагональная
матрица с собственными числами матрицы
A
по диагонали
(?!). В итоге
![]() ,
где сопрягающая матрица T
,
где сопрягающая матрица T![]() ортогональна:
ортогональна:
![]() .
.
Теорема доказана.
Примеры:
1. Если h
: R2
R2
, где h(x,
y)
= (x
+ y
; x
+ y),
то в стандартном базисе [h]e
= A
=
![]() .
Для нахождения её диагональной формы
найдём собственные числа и собственные
векторы.
.
Для нахождения её диагональной формы
найдём собственные числа и собственные
векторы.
1. Решаем характеристическое уравнение:
|I2
– A|
=
![]() = (
– 1)2
– 1 = (
– 2)
= 0.
= (
– 1)2
– 1 = (
– 2)
= 0.
Таким образом, 1 = 2, 2 = 0.
2. Находим собственные векторы, решая системы (iI2 – A)v = 0 (i = 1, 2).
а)
1
= 2:


v
=
v
= ![]() ,
v2
0.
,
v2
0.
б)
2
= 0:


v
=
v
= ![]() ,
v2
0.
,
v2
0.
3.
Находим базис из собственных векторов
и нормируем его: b1
= ![]() , b2
=
, b2
= ![]()
4. Составляем из базисных векторов сопрягающую матрицу:
T
= ![]() , T
–1 = T
t
=
, T
–1 = T
t
= ![]() .
.
5. Находим диагональный вид матрицы:
T
–1AT
= ![]() .
.
2. Если h : R3 R3 , где
h(x, y, z) = (x + y ; x + y + z ; y + z),
то
в стандартном базисе [h]e
= A
=
 .
Для нахождения её диагональной формы
найдём собственные числа и собственные
векторы.
.
Для нахождения её диагональной формы
найдём собственные числа и собственные
векторы.
1. Решаем характеристическое уравнение:
|I3
– A|
=
 = (
– 1)3
– 2(
– 1)
=
(
– 1)(2
– 2
–
1)
= 0.
= (
– 1)3
– 2(
– 1)
=
(
– 1)(2
– 2
–
1)
= 0.
Таким
образом, 1
= 1, 2
= 1 +
![]() ,3
= 1 –
,3
= 1 –
![]() .
.
2. Находим собственные векторы, решая системы (iI2 – A)v = 0 (1 i 3).
а)
1
= 1:


v
=
v
= ![]() ,
v3
0.
,
v3
0.
б)
2
= 1 +
![]() :
:
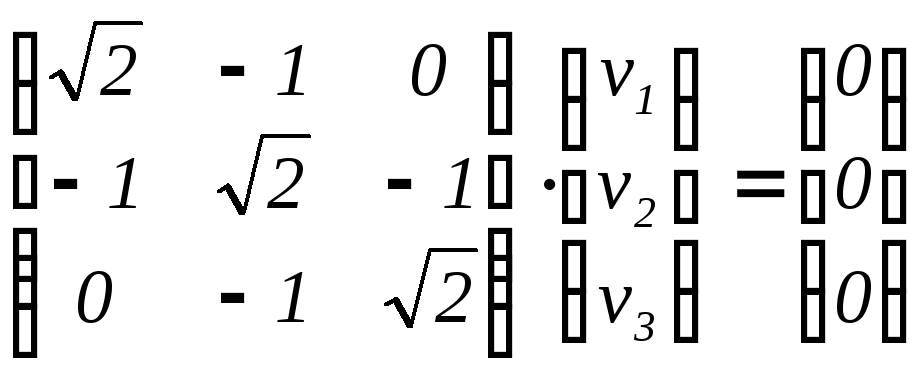

v
=
v
= 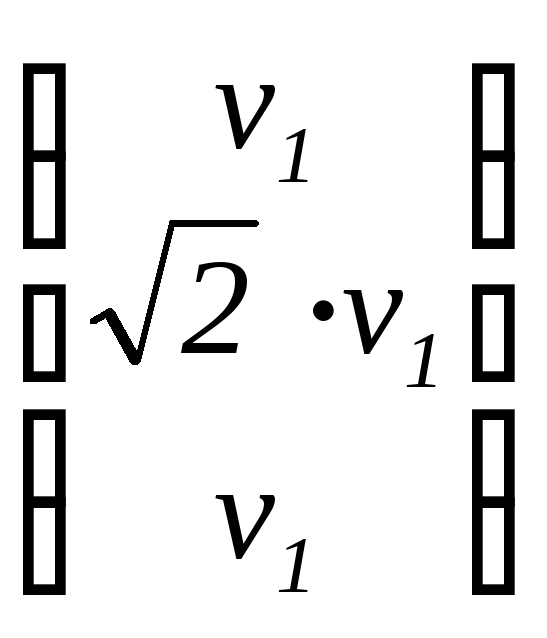 ,
v1
0.
,
v1
0.
в)
3
= 1 –
![]() :
:
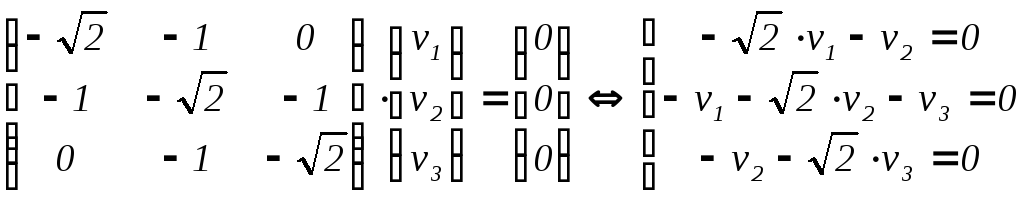 ,
v
=
,
v
=  ,
v1
0.
,
v1
0.
3. Нормированный базис из собственных векторов:
b1
=
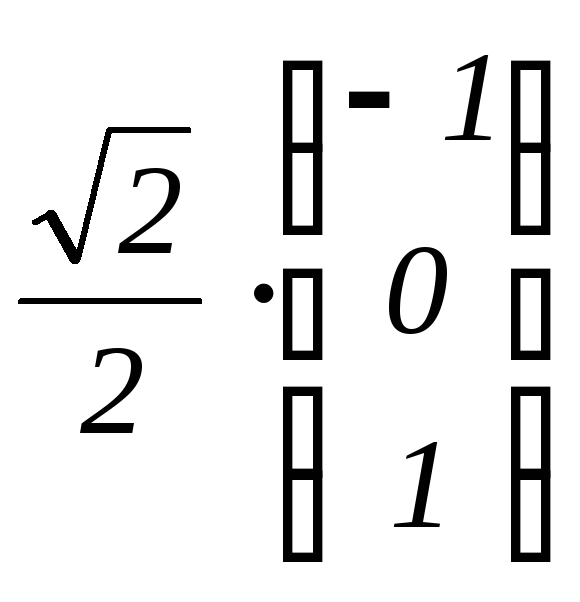 ,
b2
=
,
b2
=
 ,
b3
=
,
b3
=  .
.
4. Составляем из базисных векторов сопрягающую матрицу:
T
=  , T
–1 = T
t
=
, T
–1 = T
t
=
 .
.
5. Находим диагональный вид матрицы:
T
–1AT
=  =
=
=
 .
.
