3.2. Позиційні системи числення

Позиційними системами числення називають такі, алфавіт яких має скінчену кількість символів, причому значення кож­ної цифри в числі визначається не тільки її написанням, але й знахо­диться в строгій залежності від позиції в записі числа.

Позиційні системи числення мають ряд переваг відносно непозиційних, основною з яких є зручність виконання арифметичних операцій.

У загальному вигляді число А в позиційній системі числення може бути записано таким чином:

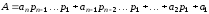, (3.1)

де – цифра-го розряду числа, причому є базою системи числення;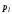– основа системи числення;– вага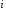-го розряду числа.

Як бачимо, такі системи будуються не тільки за принципом ади­тивності, але й за принципом мультиплікативності, тобто кількісний еквівалент числа визначається як сума сусідніх цифр зі своїми вагами.

Позиційні системи числення, в свою чергу, поділяються на ряд підкласів (рисунок 3.1). У неоднорідних позиційних системах числення не залежать один від іншого та можуть набувати будь-які значення, ці системи ще називають системами зі змішаною основою. У таких системах числення в кожному 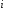-му розряді кількість допустимих символів може бути різною, при цьому, де– основа системи числе­ння в-му розряді. Прикладом неоднорідної позиційної системи числення є система числення часу.

Однорідні позиційні системи числення є частинним випадком позиційних систем числення при 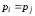для всіхта, тобто в них ваги окремих розрядів є рядом членів геометричної прогресії зі знаменником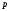. Тому число в однорідних системах може бути записано у вигляді поліному

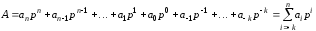, (3.2)

де , а знаменник геометричної прогресії має назву основи системи числе­ння. Очевидно, що основою однорідної позиційної системи може бути будь-яке ціле число, оскільки в означенні позиційних систем числення не накладено ніяких обмежень на величину основи. Тому можлива нескінченна множина позиційних систем числення.

Зазвичай число в однорідній позиційній системі записується у скороченому вигляді

,

а назву системи визначає її основа: десяткова, двійкова, вісімкова тощо.

Для будь-якої позиційної системи числення справедливо, що її основа зображується символами 10 у своїй системі, тобто будь-яке число в своїй системі можна записати символами цієї системи у вигляді

.

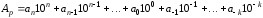Правильний дріб у системі числення буде мати вигляд

або

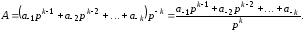(3.3)

Кодовані позиційні системи числення – це такі, в яких цифри однієї системи числення кодуються за допомогою цифр іншої системи, а число в загальному вигляді записується так:

(3.4)

де – основа системи числення, символами якої коду­ються числа;– основа початкової системи числення.

При побудові кодованих позиційних систем як ваги розрядів можуть бути вибрані члени геометричної прог­ресії (тобто ваги однорідної позиційної системи числення) та довільні числа. У першому випадку системи називають кодованими системами числення з природними вагами розрядів, у другому – зі штучними вагами розрядів.

Перевагою систем числення спеціального призначення, що створені для спрощення або прискорення обчислень у цифрових пристроях, є простота алгоритмів виконання деяких арифметичних операцій, недоліком – необхідність переведення з класичних позиційних систем у спеціальні. Їх використовують для реалізації деяких обчислювальних процесів, у яких не вимагається змінювати систему числення при введенні та виведенні даних, або ця зміна досягається простими засобами.

Наприклад, позиційні системи числення з від’ємною ос­новою дають змогу подати без знака будь-яке натуральне чис­ло, додатне або від’ємне. Однією з таких систем є зрівноважена трійкова система числення, тобто система за основою 3 з цифрами +1, 0, -1 (або ). Приклади записування чисел у цій системі:;;.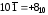

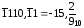Перевагами зрівноваженої трійкової системи є:

• знак числа задається його найбільш значущою (старшою) ненульовою цифрою;

• перехід до числа з протилежним знаком відбувається заміною всіх 1 на та навпаки;

• операція заокруглення до найближчого цілого зводиться до відкидання дробової частини.

Додавати в цій системі дуже просто, якщо врахувати, що 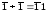,. Віднімання зводиться в переході до числа, що є протилежним за знаком, із наступною операцією додавання. Правила множення на +1 звичайні, а при множені назнак добутку змінюється на протилежний.

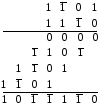
Приклад 3.1. Помножити на:

У символічних системах, на відміну від позиційних, цифри є символами, кожен з яких окремо ніяк не ха­рактеризує яке-небудь число. Визначеним комбінаціям цифр умовно поставлені у відповідність визначені числа. Прикладами символічних систем числення є знакологарифмічна система числення та система представлення чисел у залишках або сис­тема залишкових класів (СЗК).

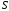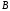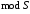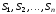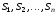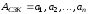Якщо цілим числам та відповідає один і той самий залишок від ділення на третє число , то числатаназивають такими, що є порівняльними за, це відображається записом. Число в СЗК зображується у вигляді залишків від ділення заданого числа на ряд взаємно простих чисел . При цьому утворюється число з вагами розрядів, що відповідно дорівнюють, тобто, дета, де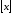– ціла частина. Отже,. Залишок називають також вирахуванням числа А за модулем .

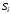В СЗК порозрядними є операція рахунку, а також операції додавання, віднімання та множення. СЗК використовуються в спеціалізованих цифрових пристроях, в яких діапа­зон початкових чисел і проміжних результатів строго фіксований та операція ділення практично відсутня.