3. Подання інформації в комп’ютерних системах. Системи числення

• Основи систем числення

• Переведення чисел з однієї системи числення в іншу

• Двійкова, вісімкова та шістнадцяткова системи числення

• Форми подання чисел у комп’ютерних системах

3.1. Основи систем числення

Системою числення називається метод подання (зображення, записування) чисел, який є спеціальною формальною мовою, алфавітом якої є множина символів, що називаються цифрами, а синтаксисом – правила, що дають змогу однозначно здійснити записування чисел. Подання числа в певній системі числення називають кодом числа у цій системі числення. Коротко число подається таким чином:

.

Окрему позицію в зображенні числа прийнято називати роз­рядом, а номер позиції – номером розряду. Число розрядів у записі числа називається розрядністю числа. У технічному аспекті розрядність інтерпретується як довжина розрядної сітки. Якщо алфавіт має 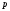різних значень, то розрядв числі розглядається як-та цифра, якій може бути при­своєно одне із значень.

Кожній цифрі даного числаА однозначно відповідає її кількісний (числовий) еквівалент – . Кількісний еквівалент коду (запису) числаА у визначеній системі числення, є деякою функцією числових еквівалентів усіх його цифр, а саме:

.

Очевидно, що для будь-якої скінченної розрядної сітки кількісний еквівалент числа А буде набувати значення від мінімального до максимального значення.

Діапазон подання чисел у даній системі числення – це інтервал числової вісі, що знаходиться між максимальним та мінімальним числами, при заданій розрядності (довжині розрядної сітки)

.

Існує багато методів зображення чисел циф­ровими знаками. Однак із практичної точки зору будь-яка система числення повинна забезпечувати:

• можливість подання будь-якого числа в заданому діапазо­ні чисел;

• однозначність подання;

• компактність та простоту записування чисел;

• легкість оволодіння системою, а також простоту й технічну зручність опе­рування нею.

Залежно від способу записування чисел та способу обчислення їх кількісного еквівалента, системи числення можна класифікувати згідно з рисунком 3.1 [15].

Рисунок 3.1. Класифікація систем числення

Переважно системи числення будують за таким принципом:

,

де запис числа в системі з базисом;– база або по­слідовність цифр системи числення з-тим алфавітом;– базис системи числення (сукупність ваг окремих роз­рядів числа).

База системи числення може бути додатною, тоді в ній як значення цифр використовується набір 0, 1,…, . Вона може бути також змішаною й тоді в ній поруч з додатними цифрами знаходяться й від’ємні. Наприклад, для симетрич­ної бази з нулем кількість додатних значень цифр дорівнює кількості від’ємних. Значення цифр алфавіту в цьому випадку при(тобто при непарній основі) формують таку множину:

.

Основою системи числення називається кількість різних символів (цифр), що можуть використовуватися у кожному з розрядів числа для його зображення в даній системі числення.

Системи числення зі змішаною базою можуть бути й при парній основі, але тоді можливе або застосування симетричних алфа­вітів без нуля (наприклад, при можливий алфавіт +1, -1), або алфавітів, в яких кількість від’ємних значень цифр не дорівнює кількості додатних (наприклад, приможливий алфавіт -1, 0, 1, 2).

Базис системи числення – це сукупність ваг окремих розрядів системи числення. Наприклад, базис десяткової системи є послідовністю: 1, 10, , …,. Вага роз­ряду числа в будь-якій системі числення – це відношення . Тому цифру розряду з більшим значеннямназивають більш значущою, ніж цифру розряду з меншим .

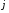Непозиційними системами числення називають такі системи числення, алфавіт яких має необмежену кількість символів (цифр), при­чому кількісний еквівалент будь-якої цифри сталий і залежить тільки від її графічного написання, але не від позиції в числі. Такі системи будують за принципом адитивності, тобто кількісний еквівалент числа визначається як сума цифр, що стоять поруч:

,

де – символи, що утворюють базис системи.

Найвідомішими представниками непозиційних систем числення є ієрогліфічні та алфавітні. Ієрогліфічні системи числення – це такі системи числення, в яких кожна цифра подана своїм символом, значком або ієрогліфом. Алфавітні системи числення – це системи числення, в яких буквам (всім або тільки деяким) приписуються числові значення, які, зазвичай, відповідають порядку букв в алфавіті. Переважно перші дев’ять букв отримують значення від 1 до 9, наступні дев’ять – від 10 до 90 й т.д. Для запису числа записуються букви, сума значень яких виражає це число.

До основних недоліків непозиційних систем числення слід віднести:

• відсутність нуля;

• необхідність використання нескінченної кількості символів;

• складність арифметичних дій із числами.