Лекции _ Вышка

P ( X - a < 3σ ) » 1

Равномерное распределение

Определение: Закон распределения называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.

Найдем плотность вероятности равномерного распределения

Понятию равномерного распределения на [a,b] соответствует представлению о выборе точки на отрезке [a,b] “наудачу”.

Найдем числовые характеристики равномерного распределения.

Математическое ожидание:

63

Показательное распределение

Определение: Показательным (экспоненциальным) называют распределение непрерывной случайной величины X , которое описывается плотностью

(рис.2).

Как видно, показательное распределение зависит от одного параметра λ . Можно показать, что функция распределения будет иметь вид (рис.2):

Показательное распределение является единственным непрерывным распределением, обладающим тем свойством, что для любых чисел x1 и x2 выполняется неравенство

P (X > x1 + x2 ) = P( X > x1 )P( X > x2 ) (свойство отсутствия последействия). Указанным свойством в значительной мере объясняется та роль, которую показательное распределение играет в теории массового обслужива-

64

Рис. 2

ния, где предполагается показательный закон распределения времени.

Числовые характеристики показательного распределения.

Найдем математическое ожидание

D(X ) = λ12 – дисперсия показательного распределения

Среднеквадратическое отклонение:

X D X 1 ,

Пример: Найти математическое ожидание, дисперсию и среднеквадратиче-

Лекция 13

Функция надёжности. Вероятность попадания в заданный

интервал показательно распределённой случайной величины. Понятие о системе двух случайных величин. Функция распределения двумерной случайной величины

Функция надёжности.

вероятности безотказной работы устройства в течении времени t , если время безотказной работы имеет показательное распределение.

Пример: Время безотказной работы устройства распределено по показательному закону f (t) = 0,02×e-0,02t при t ³ 0 ( t – время). Найти вероятность того, что элемент проработает безотказно 100 часов.

Решение: Вероятности безотказной работы устройства в течении времени t =100 определяется функцией R t при t 100

R(t) = e-λt = e-0,02×100 = e-2 = e12 = 0,13534

Вероятность попадания в заданный интервал показательно распределённой случайной величины.

Пусть случайная величина X распределена по показательному закону

Найдем вероятность попадания случайной величины в интервал (α, β ) .

Таким образом, получаем формулу

P(a < X < b) = e−λa - e−λb

Понятие о системе двух случайных величин.

Мы рассматривали случайную величину X , возможные значения которой определяются одним числом. Такие случайные величины называются одномерными случайными величинами

Определение: Двумерной случайной величиной (X ,Y ) называется система

двух случайных величин, каждая из составляющих (компонентов) которых является одномерной случайной величиной.

Закон распределения двумерной случайной величины.

Определение: Законом распределения дискретной двумерной случайной величины (X ,Y ) называется перечень её возможных значений

Функция распределения.

Геометрически это равенство можно трактовать так: F(x, y) есть вероятность того, что случайная точка ( X ,Y ) попадет в бесконечный квадрат с вершиной (x, y) , расположенный левее и ниже этой вершины (рис.3).

Свойства функции распределения

1) Значения функции F(x, y) удовлетворяют двойному неравенству

0£ F(x, y) £1

2)Функция F(x, y) является неубывающей по каждой своей координате, т.е.

Если x2 > x1 , то F(x2 , y) ³ F(x1 , y) , Если y2 > y1 , то F(x, y2 ) ³ F(x1 , y1 ) .

3) Имеют место предельные соотношения

б) При x → ∞ функция распределения системы двух случайных величин становится функцией распределения Y

lim F(x, y) = F2 (y) , где F2 (y) – функция распределения Y .

x→+∞

68

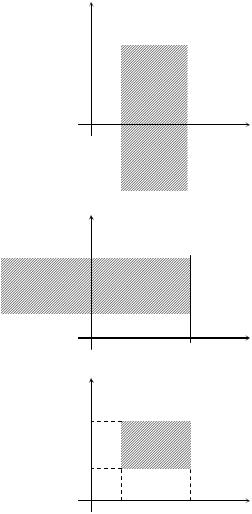
Вероятность попадания двумерной случайной величины в полуполосу и прямоугольник:

горизонтальную полуполосу вычесть вероятность попадания в вертикальную полуполосу

69

P(x1 £ X < x, y1 £ Y < y2 ) = [F(x2 , y2 ) - F(x1 , y2 )]-

+[F(x2 , y1 ) - F(x1 , y1 )]

Пример: Задана интегральная функция двумерной случайной

прямоугольник, ограниченный прямыми x 0,x /4,y /6,y /3 .

Решение: Воспользуемся выше доказанной формулой

P(0 £ X < π / 4,π / 6 £ Y < π /3) = [F(π / 4,π / 3) - F(0,π / 3)]-

Плотность распределения двумерной случайной величины

Определение: Плотностю распределения независимой случайной величины (X ,Y ) называется смешанная производная 2-го порядка от функции распределения:

f (x, y) = ¶2 F(x, y)

¶x¶y

Функция распределения выражается через плотность с помощью двойного интеграла

x y

F(x, y) = ò ò f (x, y)dxdy

−∞ −∞

Свойства плотности распределения

1) f (x, y) ³ 0 .

+∞ +∞

2) ò ò f (x, y)dxdy = 1.

−∞ −∞

70

Лекция 14

Элементы теории корреляции.Зависимость и независимость одномерных случайных величин. Коэффициент корреляции.

Понятие о многомерной случайной величине.

Во многих задачах требуется оценить зависимость между двумя и более случайными величинами. Например, хотят определить, существует ли связь между курением и продолжительностью жизни, между умственными способностями и успеваемостью и так далее.

Рассмотрим зависимость между двумя случайными величинами X и

Y. Эта зависимость может быть трех типов:

1)величины независимы.

2)между ними существует функциональная зависимость.

3)между ними существует статистическая зависимость.

Определение: Две случайные величины X и Y называются независимыми, если закон распределения одной случайной величины не зависит от закона распределения другой случайной величины.

Например, X – рост студента, Y – его оценка на экзамене и так далее.

Функциональная зависимость.

Определение: Если каждому возможному значению случайной величины X соответствует единственное возможное значение случайной величины Y , то Y является функцией от X : Y = ϕ(X ) .

Например:

Реализатор на рынке получает 2% от суммы реализованных товаров. Пусть X – сумма, на которую проданы товары – имеет распределение:

Тогда Y – полученные реализатором деньги – будет иметь распределение

Как видим, эти случайные величины связаны между собой строгой функциональной зависимостью Y = 0,02X

71