Лекции _ Вышка

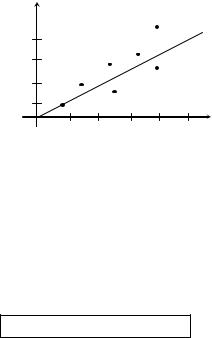
Статистическая зависимость

Определение: Две случайные величины X и Y называют статистически зависимыми, если изменение распределения одной из случайных величин влечёт за собой изменение распределения другой случайной величины.

Например, X – рост студента, Y – масса. Строгой функциональной зависимости нет, так как определённый рост не отвечает определённой массе.

увеличением роста растет и масса (рис.1)

y

80

70

60

Рис. 1

Числовой характеристикой, которая служит мерой того, насколько одна случайная величина зависит от другой, служит коэффициент корреляции.

Коэффициент корреляции

Определение: Корреляционным моментом Mxy двух случайных величин

X и Y называется математическое ожидание произведения их отклонений:

μxy = M {[X - M (X )][Y - M (Y )]}

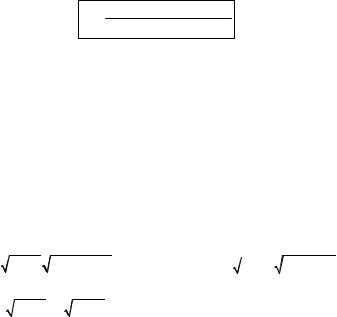
Для непрерывных – по формуле

+∞ +∞

μxy = ò ò (x - M (X ))( y - M (Y )) f (x, y)dxdy

−∞ −∞

Т. Корреляционный момент двух независимых случайных величин равен нулю.

Доказательство:

Так как X и Y – независимые случайные величины, то X - M (X ) и Y - M (Y ) тоже независимые случайные величины. Тогда

M {[ X - M (X )][Y - M (Y)]} = M [ X - M (X )] M [Y - M (Y )] = 0

Определение: Коэффициентом корреляции двух случайных величин называется величина, определяемая по формуле

r= M (X ,Y) - M (X )M (Y)

σ(X )σ (Y )

Если X и Y независимые, то M (X ,Y ) = M (X )M (Y) и r = 0 .

Определение: Величины X и Y называются некоррелированными, если коэффициент корреляции равен нулю r = 0 .

Т. Если между случайными величинами существуют функциональная зависимость, то r = ±1.

Доказательство:

Докажем для случая, когда между случайными величинами существует

73

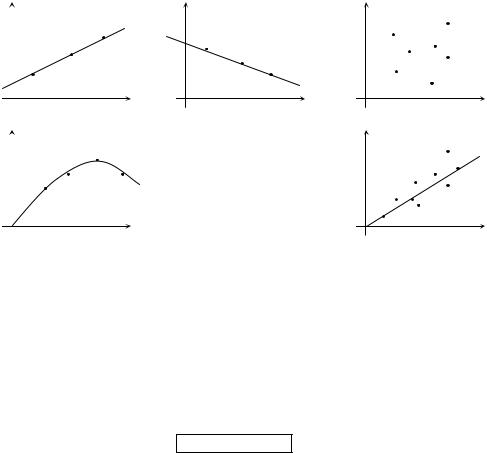
Если r положительное (положительная корреляция), то с ростом случайной величины X растёт и Y , если r отрицательное (отрицательная корреляция), то Y с ростом X уменьшается.

На графиках (рис.2) показаны примеры различных значений коэффициента корреляции.

Рис. 2

Зависимость или независимость случайных величин X и Y можно проверить с помощью фунции распределения двумерной случайной величины X,Y . Докажем следующую теорему.

Т. Для того, чтобы случайные величины X и Y были независимыми необходимо и достаточно, чтобы функция распределения двумерной случайной величины (X ,Y ) была равна произведению функций

распределения величин X и Y .

F(x, y) = F1 (x)F2 (y)

Доказательство:

a) докажем необходимость

Пусть X и Y – независимые случайные величины. Рассмотрим событие X < x, Y < y . По определению двумерной функции распределения

F(x, y) = P(X < x,Y < y) = P(X < x)P(Y < y) = F1 (x)F2 (y)

б) докажем достаточность

Пусть выполняется соотношение F(x, y) = F1 (x)F2 (y) . Тогда

74

Следствие: Для того, чтобы случайные величины X и Y были независимыми необходимо и достаточно, чтобы плотность распределения двумерной случайной величины (X ,Y ) была равна произведению плотностей

распределения величин X и Y .

f (x, y) = f1 (x) f2 (y)

Доказательство:

а) необходимость. Пусть X и Y - независимые. Найдем плотность распределения двумерной случайной величины

По доказанной выше теореме отсюда будет следовать, что случайные величины X и Y независимы

Многомерные случайные величины.

Определение: n - мерной случайной величиной ( n -мерным случайным вектором) называется совокупность n случайных величин.

X = (X1 , X2 ,..., Xn ) , Xi – одномерные случайные величины.

Функция распределения n -мерной случайной величины равна:

А функция распределения находится через плотность через n - кратный

76

Элементы математической статистики

Лекция 15

Характеристики выборки. Задачи математической статистики. Генеральная и выборочная совокупности. Статистическое распределение выборки. Эмпирическая функция распределения и ее свойства. Полигон и гистограмма

Чтобы установить закономерности, которым подчиняются массовые случайные явления, производят сбор статистических данных и их изучение на основе методов теории вероятностей. Методами сбора данных и их математического анализа занимается математическая статистика.

Математическая статистика – наука о математических методах сбора, систематизации и обработки статистических данных для получения научных

ипрактических выводов.

Возникла математическая статистика вместе с теорией вероятностей в XVII

в. Родоначальниками являются Якоб Бернулли (1654-1705), Пьер Симон Лаплас(1749-1827), Симеон Дени Пуассон (1781-1840). В XIX - начале XX века математическая статистика получила развитие в работах Пафнутия Чебышева (1821-1894), Александра Ляпунова (1857-1918), Карла Фридриха Гаусса (1777-1855) и других ученых. В XX веке ее развитие связано с такими именами как Эгон Шарп Пирсон (1895-1980), Всеволод Иванович Романовский (1879-1954), Андрей Николаевич Колмогоров (1903-1987) и другими.

Задачи математической статистики

Задачи математической статистики состоят в том, чтобы на основании знания некоторых свойств подмножества элементов, взятых из некоторого множества, сделать утверждения о свойствах всего множества, называемого генеральной совокупностью. Задачи можно разделить на два типа.

Первая задача – указать способы сбора и группировки статистических данных (планирование эксперимента).

Вторая задача – разработать методы их анализа в зависимости от цели:

а) оценка неизвестной вероятности, например, вероятности рождения мальчика; оценка неизвестной функции распределения, оценка параметров распределения, вид которого известен; оценка зависимости одной случайной величины от другой.

76

б) проверка гипотез о характере распределения случайной величины или его параметров.

Генеральная и выборочная совокупности

Пусть требуется изучить совокупность некоторых однородных объектов относительно определенного качественного или количественного признака. Например, для партии деталей качественным признаком может быть стандартность, количественным – диаметр. Иногда производится сплошное обследование, то есть проверяется каждая деталь. Но это очень сложно и трудно. Поэтому выбирают ограниченное число объектов и подвергают их изучению.

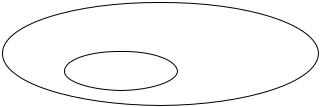
Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов.

генеральная совокупность

выборка

Рис. 1

Генеральной совокупностью называется совокупность объектов, из которых производится выборка (рис.1).

Объёмом (генеральной или выборочной совокупности) называют количество объектов этой совокупности.

Например, из 1000 деталей отобрали 100, тогда объём генеральной совокупности N = 1000 , объём выборки n = 100 .

Часто при вычислении предполагают, что объём генеральной совокупности стремится к бесконечности.

Характеристики выборки

После того, как объект отобран и над ним произведено наблюдение, он может быть возвращён либо не возвращён в генеральную совокупность. Повторной выборкой называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

77

Чтобы можно было правильно судить о всей генеральной совокупности, выборка должна быть правильно отобрана или быть репрезентативной

(представительной).

В силу закона больших чисел это будет тогда, когда выборка будет случайной.

Способы отбора

1) Отбор, не требующий расчленения генеральной совокупности на части:

а) простой случайный бесповторный отбор.

При таком отборе объекты извлекаются по одному из всей совокупности. На практике это можно реализовать, например, написав номера от 1 до N , перемешать их и вытащить наугад n карточек, далее взять номера объектов, соответствующие номерам карточек.

б) простой случайный повторный отбор.

Проделывают тоже самое, но карточки возвращаются, перед тем, как взять новую карточку. Часто пользуются готовыми таблицами случайных чисел. 2) Отбор, при котором генеральная совокупность делится на части:

а) типический отбор.

При типическом отборе объекты разделяют по типу. Например, если детали изготовлены на нескольких станках, то отбор производят из продукции каждого станка в отдельности.

б) механический отбор.

Все детали делятся на группы и из каждой группы выбирают один объект. Например, берут каждую пятую деталь, каждую десятую и т.д.

в) серийный отбор.

Объекты отбирают не по одному, а сериями. Например, если детали изготавливались несколькими станками, то отбирают детали 1 и 2 станка и подвергают сплошному обследованию.

На практике, как правило, эти методы комбинируют.

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка объёма n . X

– некоторый количественный признак (например, диаметр). Пусть X для данной выборки имеет значения x1 , x2 ,..., xn , называемые вариантами выборки. Последовательность вариант, записанных в возрастающем порядке называется вариационным рядом. Пусть значение x1 встретилось n1 раз, значение x2 - n2 раза, ..., xn - nk раз (k £ n) , тогда ni называются

относительными частотами

78

Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.

Статистическое распределение можно также задать в виде последовательности интервалов и соответствующих им частот. В качестве частоты интервала принимают сумму частот вариант, попавших в этот интервал. Как правило, статистическое распределение задают в виде таблицы.

k

åni = n

i =1

Эмпирическая функция распределения

Пусть известно статистическое распределение частот признака X . Пусть nx – число наблюдений, при которых наблюдалось значение признака, меньшее x ; n – общее число наблюдений (объем выборки). Тогда относительная частота события X < x равна nx / n , которая является функцией от x .

Определение: Эмпирической функцией распределения называется функция

F* (x) , определяющая для каждого значения x относительную частоту события X < x .

где nx – число вариант, меньших x ; n – объем выборки

Свойства эмпирической функцией распределения

79

Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.

Пример: Построить эмпирическую функцию по данному распределению выборки.

Найдем объем выборки: 12+18+30=60.

1.x ≤ 2 , F* (x) = 0 (так как нет вариант, меньше 2)

2.2 < x ≤ 6 , F* (x) = 1260 = 102 (число вариант, меньше 6 равно 12)

3.6 < x ≤ 10 , F* (x) = 3060 = 12

4.x > 10 , F* (x) = 6060 =1

Таким образом, эмпирическая функция распределения будет иметь вид

(рис.2)

Рис. 2

80