Лекции _ Вышка

Пусть количественный признак X распределен нормально. Требуется оценить неизвестное среднеквадратическое отклонение по исправленному выборочному среднеквадратическому отклонению S . То есть, найти доверительный интервал, покрывающий параметр σ с надёжностью γ :

S(1- q) < σ < S(1+ q)

q = q(γ ,n) ищем по таблице

S = nn-1 Dв .

Замечание: Если q > 1 , то, учитывая, что σ > 0 , имеем:

0 < σ < S(1+ q)

Пример1: Количественный признак X распределен нормально, n = 25 , S = 0,8 . Найти доверительный интервал, покрывающий генеральное среднеквадратичное отклонение σ с надёжностью 0,95.

Решение:

Согласно условию задачи γ = 0,95; n = 25; q = q(0,95;25) = 0,32 По формуле для оценки неизвестного σ имеем

0,8(1- 0,32) < σ < 0,8(1+ 0,32) 0,544 < σ <1,056

Пример 2: Произведено 12 измерений одним прибором (без систематических ошибок) некоторой физической величины, причем исправленное среднее квадратическое отклонение S случайных ошибок измерений оказалось равным 0,6. Найти точность прибора с надежностью 0,99.

Решение:

Точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала, покрывающего параметр σ с заданной надежностью

γ = 0,99 .

90

По данным γ = 0,99 и n = 12 по таблице найдем q = 0,9 . Подставив S = 0,6 и q = 0,9 в соотношение (**), окончательно получим

0,06 < σ < 1,14

91

Лекция 18

Выборочный коэффициент корреляции. Условные средние.

Выборочные уравнения регрессии. Корреляционная таблица. Простейшие случаи криволинейной корреляции

Точечной характеристикой коэффициента корреляции служит выборочный коэффициент корреляции.

Если наблюдаемые значения признака X ,

Доверительный интервал для оценки генерального коэффициента корелляции нормального распределения

Можно показать, что если случайные величины X и Y имеют нормальное распределение, то для оценки генеральной корреляции служит интервал:

Формула применяется при объеме выборки n ³ 50 .

Условные средние.

Определение: Условным средним yx называется среднее арифметическое

наблюдаемых значений признака Y при условии, что признак X примет значение, равное x .

Найдем условные средние при следующих наблюдаемых значениях X иY

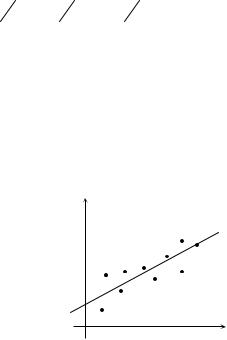
Выборочные уравнения регрессии.

y

x

Рис. 1

выборочным уравнением регрессии X на Y . Если величины X и Y имеют линейную корреляцию, то линией регрессии будет прямая (рис.1).

92

Выборочное уравнение прямой линии регрессии.

Уравнением регрессии Y на X является зависимость yx = f *(x) . Пусть выборочное уравнение регрессии является линейным, то есть имеет вид yx = ρyx x + b . Найдем b . Запишем условные средние Y при различных значениях признака X .

Отсюда следует, что b = yв - ρyx × xв . Тогда yx = ρyx × x + yв - ρyx × xв . Запишем это уравнение в виде

yx - yв = ρyx (x - xв ) .

Можно показать, с помощью метода наименьших квадратов можно найти коэффициент ρyx , который называется коэффициентом регрессии.

Аналогично, выборочное уравнение прямой линии регрессии X на

Y .

xy - xв = rв σвx ( y - yв ) σвy

93

выборочный коэффициент корреляции является средним геометрическим коэффициентов регрессии.

Замечание 2. Уравнение прямой линии регрессии Y на X можно записать в симметричном виде:

yx −8,1 = 16 (x − 4,1)

Корреляционная таблица.

При большом числе наблюдений одно и то же значение x может встретиться nx раз, одно и то же значение y – ny раз, одна и та же пара чисел (x, y) может наблюдаться nxy раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты nx , ny , nxy . Все сгруппированные данные

записывают в виде таблицы, которую называют корреляционной. Поясним устройство таблицы на примере.

В первой строке таблицы указаны наблюдаемые значения признака X , в первом столбце – наблюдаемые значения признака Y . На пересечении строк

94

и столбцов находятся частоты nxy наблюдаемых пар значений признаков. В

последней строке записаны суммы частот столбцов. В клетке, расположенной в нижнем правом углу таблицы, помещена сумма всех частот.

ånxy = 60 = n; åny = n; ånx = n

Методика вычисления выборочного коэффициента корреляции по данным корреляционной таблицы.

Можно упростить вычисление выборочного коэффициента

Выборочный коэффициент корреляции вычисляется по формуле:

rв = ånuvuv - nu v nσuσv

u,v - выборочные средние u и v . σu ,σv - выборочные средние

квадратические отклонения.

x = u ×hx + C1 , y = u ×hy + C2 , σ x = σu ×hx , σ y = σv ×hy

При вычислении ånuv ×uv можно воспользоваться формулами:

Для контроля вычисляют по обеим формулам, совпадение результатов свидетельствует о правильности вычислений.

Простейшие случаи криволинейной корреляции

Определение: Если линией регрессии yx = f *(x) или xy = ϕ(y) является кривая порядка выше первого, то корреляцию называют криволинейной.

Например, yx = ax2 + bc + c (параболическая корреляция второго порядка). yx = ax3 + bx2 + cx + d (параболическая корреляция третьего порядка).

Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции, то есть установление тесноты связи между случайными величинами. Форма кривой регрессии находится методом

95

наименьших квадратов. Для оценки тесноты связи служат выборочные корреляционные отношения ηyx : 0 ≤ ηyx ≤ 1; η = σмежгруповое .

96

Лекция 19

Проверка статистических гипотез. Ошибки первого и второго рода. Критическая область. Область принятия гипотез.

Проверка гипотезы о значимости выборочного коэффициента корреляции.

Проверка статистических гипотез.

Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, то имеются основания предположить, что он имеет определённый вид. То есть выдвигается гипотеза о виде распределения или о параметрах распределения.

Определение: Статистическими называются гипотезы о виде неизвестного распределения или о параметрах распределения.

Например, статистическими явлениями гипотезы:

1)генеральная совокупность распределена нормально.

2)генеральная совокупность имеет показательное распределение.

3)математическое ожидание генеральной совокупности равно 5 .

Гипотеза “ на Луне есть жизнь” не является статистической, так как не имеет отношения ни к виду распределения, ни к параметрам.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то будет принята противоречащая гипотеза.

Определение: нулевой (основной) гипотезой называют выдвинутую гипотезу

H0 .

Определение: конкурирующей (альтернативной) называют гипотезу H1 , которая противоречит основной.

Например, если нулевая гипотеза H0 : a = 4 , то H1 : a ¹ 4 .

Различают гипотезы, которые содержат одно или больше одного предположения:

Простой называют гипотезу, содержащую только одно предположение. Если λ – параметр показательного распределения, то H0 : λ = 5 – простая гипоте-

за.

Сложной гипотезой называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например: H : λ > 5 состоит из беско-

96

нечного количества простых гипотез H0 : λ = bi , где bi > 5 . Гипотеза H0 :

математическое ожидание нормального распределения равно 3 (σ неизвестно) – сложная.

Ошибки первого и второго рода.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость её проверки. Поскольку проверку производят статистическими методами, то проверку называют статистической. При проверке гипотезы может быть сделаны ошибки: отвергнута правильная гипотеза и принята неправильная.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза H0 и принята неправильная гипотеза H1 , в то время как верна гипотеза

H0 .

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза H0 , в то время как верна гипотеза H1 .

Определение: Вероятность совершить ошибку первого рода называется уров-

нем значимости α :

α = PH0 (H1 ) , где PH0 (H1 ) – вероятность принять гипотезу H1 , в то время как верна гипотеза H0 .

Наиболее часто его принимают равным α = 0,05 или α = 0,01. α = 1− γ , где γ – надежность.

Вероятность ошибки второго рода определяется параметром β :

β = PH1 (H0 ) , где PH1 (H0 ) – вероятность того, что будет принята гипотеза H0 , в то время как верной является гипотеза H1 .

Статистический критерий проверки нулевой гипотезы

Для проверки нулевой гипотезы используют специально подобранную случайную величину.

Определение: Статистическим критерием называют случайную величину K , которая служит для проверки нулевой гипотезы.

97