
Лекции _ Вышка
.pdf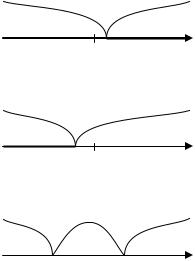
Например, если проверяют гипотезу о равенстве дисперсий двух нормально
распределённых случайных величин, то в качестве K берут: F = |
S2 |
, где |
|||
1 |
|||||
S22 |
|||||
|
|
|
|
||
S2 |
, S2 |
– исправленные выборочные дисперсии. |
|
|
|
1 |
2 |
|
|
|
|
Наблюдаемым значением Kнабл критерия K называется значение критерия, вычисленного по выборкам. Например, по двум выборкам найдены исправ-
ленные выборочные дисперсии S12 = 20, S22 = 5; F = |
20 |
= 4 . |
|
5 |
|||
|
|
Критическая область. Область принятия гипотез
Определение Областью принятия гипотезы (областью допустимых значе-
ний) называют совокупность значений критерия, при которых гипотезу принимают.
Определение Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
|
Область |
Критическая |
|
принятия |
|
a) |
решения |
область |
0 |
kкр |
k |
б) |
Область |
|
Критическая |
|
|
принятия |
|
|
область |
решения |
|
Критическими точка-
ми kкр называют точки,
которые отделяют критическую область от области принятия решения.
Правосторонней
называют критическую область, которая опре-
деляется |
неравенством |
K > kкр , |
где kкр > 0 - |
|
|
|
kкр 0 |
k |
положительное |
число |
||||
|
|
|
|
|
|
|
|
(рис.1 а). |
|
|
с) |
|
|
|
|
|
Левосторонней |
||||
|
|
|
|
|
называют |
критическую |
||||
|
|
|
|
|
|
|
|
|||
Критическая |
Область |
Критическая |
область, которая опре- |
|||||||
принятия |
деляется |
неравенством |
||||||||
область |
решения |
|
область |
K < kкр , где kкр |
- отри- |
|||||
|
|
|
|
|
|
|
|
|||
|
−k1 |
|
|
|
k |
|||||
|
0 −k2 |
цательное число (рис.1 |
||||||||
|
|
|
|
|
|
|
|
б). |
|
|
Рис. 1 |
Правосторонняя |
|
и левосторонняя области являются односторонними критическими областями.
98
Двухсторонней называется критическая область, которая определяется неравенством k1 < K < k2 , где k2 > k1 . (рис.1 с)
Если критические точки симметричны относительно нуля, то двухсторонняя критическая область определяется неравенством K > kкр .
Проверка гипотезы о значимости выборочного коэффициента корреляции.
Пусть сделаны выборки X и Y , причем выборочный коэффициент корреляции rв ¹ 0 , пусть также генеральная совокупность ( X ,Y ) распреде-
лена нормально. Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент генеральной совокупности rГ также отличен от нуля.
Поэтому возникает необходимость при заданном уровне значимости α проверить гипотезу . Если нулевая гипотеза отвергается, то это означает, что выборочный коэффициент корреляции значимо отличается от нуля, а X и Y коррелированы, т.е. связаны зависимостью. Если нулевая гипотеза будет принята, то выборочный коэффициент незначим, а X и Y некоррелированы.
В качестве критерия проверки нулевой гипотезы принимают случайную величинуT = rв 
 n − 2
n − 2

 1− rв2 . Величина T при справедливости нулевой
1− rв2 . Величина T при справедливости нулевой
гипотезы имеет распределение |
Стьюдента с k = n - 2 степенями свободы. |
||||||||
Для этого вычисляют |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Tнабл = |
rв |
|
|
|
|
|
, k = n - 2 |
|
n - 2 |
– число степеней свободы. |
||||||||
|
|
|
|
|
|||||
1- r2 |
|||||||||
|
|
|
|
в |
|
|
|||
По таблице критических точек распределения Стьюдента по заданному α и k = n - 2 находят критическую точку tкр (α,k) двусторонней крити-
ческой области.
Если Tнабл > tкрит – нулевую гипотезу отвергают, если Tнабл < tкрит – то принимают.
Сравнение двух дисперсий нормальных генеральных совокупностей
По независимым выборкам, объемы которых n1 и n2 , извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии Sx2 и Sy2 . Требуется сравнить эти дисперсии.
99
Правило1. Для того чтобы при заданном уровне значимости α проверитьт нулевую гипотезу H0 : D( X ) = D(Y ) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе надо вычислить наблюдаемое значение критерия
(отношение большей исправленной дисперсии к меньшей)
F |
= |
S2 |
|
б |
|||
Sм2 |
|||
набл |
|
и по таблице критических точек распределения Фишера-Снедекора,
по заданному уровню |
значимости α и числам степеней свободы |
k1 = n1 -1, k2 = n2 -1( k1 – |
число степеней свободы большей исправлен- |
ной дисперсии), найти критическую точку Fкр (α, k1 ,k2 ) . Если Fнабл < Fкр – нет оснований отвергнуть нулевую гипотезу. Если Fнабл > Fкр – нулевую гипотезу отвергают.
Правило2 При конкурирующей гипотезе H1 : D( X ) ¹ D(Y ) критическую точку Fкр (α / 2, k1 , k2 ) ищут по уровню значимостиα / 2 (вдвое меньшему заданного) и числам степеней свободы k1 и k2 ( k1 – число
степеней свободы большей дисперсии).
Если Fнабл < Fкр – нет оснований отвергнуть нулевую гипотезу. Если Fнабл > Fкр – нулевую гипотезу отвергают
Пример: По двум независимым выборкам, объемы которых n1 =11 и
n2 |
= 14 , извлеченным из нормальных генеральных совокупностей X и |
Y , |
найдены исправленные выборочные дисперсии Sx2 = 0,76 и |
Sy2 |
= 0,38 . При уровне значимости α = 0,05 проверить нулевую гипо- |
тезу H0 : D( X ) = D(Y )о равенстве генеральных дисперсий, при конку-
рирующей гипотезе H1 : D( X ) > D(Y ).
Решение: Найдем отношение большей исправленной дисперсии к меньшей:
F |
= |
S2 |
= |
0,76 |
= 2 |
|
б |
|
|||||
Sм2 |
0,38 |
|||||
набл |
|
|
|
По условию конкурирующая гипотеза имеет вид D( X ) > D(Y ), поэто-
му критическая область – правосторонняя.
100
По таблице по уровню значимости α = |
0,05 и числам степеней свобо- |
|
ды k1 |
= n1 −1 = 11−1 = 10 и k2 = n2 −1 =14 |
−1 = 13 находим критическую |
точку |
Fкр (0,05;10;13) = 2,67 . Так как Fнабл < Fкр – нет оснований отверг- |
|
нуть гипотезу о равенстве генеральных дисперсий. Другими словами, выборочные исправленные дисперсии различаются незначимо.
Список используемой литературы
1.Гмурман В.Е. Теория вероятностей и математическая статистика,
М., 1977, 478 с.
2.Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике, М., 1975,
3.Чистяков В. П. Курс теории вероятностей, М., Наука, 1987, 240 с.
4.Захаров В. К. , Севастьянов Б. А. , Чистяков В. П. Теория вероятностей, М., Наука, 1983, 155 с.
5.Жлуктенко В. І. , Наконечний С. І. , Савіна С.С. Теорія ймовірностей і математична статистика, Ч.1, Ч.2, 2001.
6.Теория вероятностей и математическая статистика, под ред. В. И.
Ермакова, М., 2004, 286 с.
101
