
Лекции _ Вышка
.pdf
Лекция 16
Полигон и гистограмма .Точечные оценки выборки. Смещённые и несмещённые оценки.
Полигон и гистограмма.
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
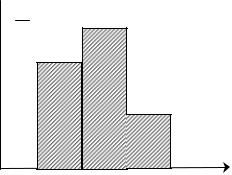
Определение: Полигоном частот называется ломаная, отрезки которой соединяют точки (x1 , n1 ) , (x2 ,n2 ),K, (xk ,nk ) . Аналогично строится полигон
hi
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
0,1 |
|
|
|
|
|
|
|
|
|
|
x |
|
0 |
2 |
4 |
6 |
8 |
10 |
|||||||
|
||||||||||||
|
Рис. 1 |
|
|
|
|
|
|
|
|
|||
относительных частот. На рис.1 изображен полигон относительных частот для распределения выборки
xi |
2 |
4 |
6 |
8 |
hi |
0,2 |
0,3 |
0,4 |
0,1 |
В случае непрерывного признака целесообразно строить гистограмму частот, для чего интервал, в котором заключены все необходимые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала ni – сумму частот вариант,
попавших в i -ый интервал.
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h , а высоты равны отношению ni / h (плотность частоты) (рис.2).
81
Площадь i -го прямоугольника равна ni , следовательно площадь
гистограммы равна объему выборки.
Аналогично определяется гистограмма относительных частот. Ее площадь равна единице.
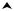 ni
ni
h
5 |
10 |
15 |
20 |
x |
|
Рис.2
Точечные оценки выборки
Точечной оценкой называется оценка, которая определяется одним числом. Точечные оценки являются аналогами числовых характеристик, которые
используются в теории вероятностей.
Определение: Выборочным средним xв |
называется среднее арифметическое |
|
|||||||||||||||||||||||
наблюдаемых значений признака X . |
|
|
|
|
|
|
|
x1 + x2 +...+ xn |
|
|
|
|
|
||||||||||||
Если все значения x , x ,..., x |
различны, то x |
= |
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 2 |
n |
|
|
|
|
|
|
|
в |
|
|
|
|
|
n |
|
|
|
|
|
|
|
||
|
|
Если значение x1 встретилось n1 |
|
|
|
|
|
|
|
|
|
x2 - |
n2 |
|
|
..., xk - |
|
||||||||
|
|
|
раз, |
значение |
раза, |
|
|||||||||||||||||||
nk |
раз (k £ n) , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k x ×n |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
xв = å |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
i=1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Представим выборочное среднее в виде. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x |
= |
x1 ×n1 + x2 ×n2 +...+ xk ×nk |
|
= x × |
n1 |
+ x |
× |
n2 |
+...+ x |
× |
nk |
|
= x ×h + x |
×h |
+ ...+ x |
×h |
|||||||||
n |
|
|
n |
n |
|||||||||||||||||||||
в |
|
|
1 n |
2 |
|
|
|
|
|
k |
|
1 |
1 |
|
2 |
2 |
k |
k |
|||||||
.
82
ni – частоты вариант, hi - относительные частоты (i =1, k)
Выборочное среднее служит приближённой характеристикой математического ожидания.
Определение: Отклонением наблюдаемого значения xi от xв называется разность между значением признака xi и выборочным средним.
Т. Сумма произведений отклонений на соответствующие частоты равна нулю
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
å(xi - xв )ni |
= 0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Докажем равенство |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi - xв )ni |
k |
|
x ×n |
k |
x ×n |
|
|
|
|
|
|||||
|
i=1 |
= å |
i |
i |
- å |
в |
|
i |
=xв - xв = 0 . Следовательно |
|||||||
|
n |
|
n |
|
|
|
||||||||||
|
i=1 |
i=1 |
|
n |
|
|
|
|
|
|||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi - xв )ni |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение: |
Выборочной |
|
|
дисперсией |
Dв |
|
называется среднее |
|||||||||
арифметическое квадратов отклонений наблюдаемых значений. |
||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi - xв )2 |
|
|
|
|
|
||||||
|
|
D = |
i=1 |
|
|
|
– если все значения различны. |
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
в |
|
n |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если наблюдаемые значения имеют частоты n1 , n2 ,..., nk , то |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi |
- xв )2 |
×ni |
|
|
|
|
|
|
|
|
|
|
|
|
D = |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
в |
n |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определение: Выборочным средним квадратическим отклонением
(стандартом) называется квадратный корень из выборочной дисперсии.
σв = 
 Dв
Dв
Формула для вычисления выборочной дисперсии
83

Докажем, что выборочная дисперсия может быть вычислена по формуле
|
|
|
|
|
|
|
|
|
|
|
|
|
Dв = |
|
|
|
-[xв ]2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
xв2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
В развернутом виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
D = |
x2 |
×n + x2 |
×n |
+ ...+ x2 |
×n |
|
- |
é x ×n + x |
|
×n |
2 |
+...+ x |
×n |
ù |
2 |
. |
||||||||||||||||
|
|
1 |
1 |
2 |
2 |
|
k |
|
|
k |
|
ê |
1 1 2 |
|
|
|
|
k |
k |
ú |
|
|||||||||||||
|
|
в |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
û |
|
|
||||
Доказательство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
k |
(x2 |
- 2x × x + x 2 )×n |
k |
|
|
x |
2 |
|
×n |
|
|
n |
x ×n x 2 k |
|
|
|
|
|||||||||||||||
Dв = å |
|
i |
|
i |
в |
|
в |
i |
= å |
i |
|
|
i |
|
- 2xв å |
i |
|
i |
+ |
в |
åni |
= |
|
|||||||||||
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|||||||||||||||||
|
|
i =1 |
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
i =1 |
|
n |
|
|
i=1 |
|
|
|
|||||||||
k x2 |
×n |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
å |
i |
i |
|
- 2xв2 + xв2 = xв2 |
-[xв ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Смещённые и несмещённые оценки.
Определение: Генеральной средней xГ называется среднее арифметическое значений признака генеральной совокупности.
Если все значения x1 , x2 ,K, xN различны, то генеральная средняя определяется по формуле
x= x1 + x2 +...+ xN
ГN
Если все значения x1 , x2 ,K, xk имеют частоты N1 , N2 ,K, Nk , то генеральная средняя определяется по формуле
x = x1 N1 + x2 N2 + ...+ xk Nk |
|
Г |
N |
|
|
Аналогично выборочной дисперсии определяется генеральная дисперсия.
Одна из задач, которую ставит перед собой математическая статистика – это
по выборочным средним xв и |
выборочной |
дисперсии |
Dв |
оценить |
|||
генеральную среднюю xГ |
и генеральную дисперсию |
DГ . |
|
|
|||
Пусть θ – |
неизвестный |
параметр |
генеральной |
совокупности |
(например, |
||
генеральное |
среднее или |
генеральная дисперсия), |
а θ * – |
его |
оценка по |
||
|
|
|
84 |
|
|
|
|
выборке. Величину θ * можно рассматривать как случайную величину, зависящую от выборки. Возможные значения этой величины соответствуют различным выборкам. По этим возможным значениям можно найти математическое ожидание. Тогда
Определение: Несмещенной называют статистическую оценку θ * , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
M (θ* ) = θ
Определение: Смещенной называется оценка, математическое ожидание которой не равно оцениваемому параметру .
Можно показать, что M (xв ) = xГ , то есть xв – несмещённая оценка xГ . В отличие от этого, выборочная дисперсия является смещенной оценкой
генеральной дисперсии. M (Dв ) = nn-1 DГ . Чтобы избежать смещения, вводят понятие исправленной дисперсии:
|
S2 |
= |
|
|
n |
|
|
D |
|
– исправленная дисперсия. |
|||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
n -1 |
в |
|
|
|
|
|
|
|
|
|
|||||
Таким образом, введенная дисперсия будет являться уже несмещенной |
|||||||||||||||||||
|
|
|
|
оценкой, так как M (S2 ) = DГ . |
|
|
|||||||||||||
|
|
|
|
n |
|
|
k |
|
(x - x )2 ×n |
k (x - x )2 |
×n |
||||||||
S2 = |
|
|
|
|
å |
|
|
i в |
i |
= å |
|
i в |
i |
|
|||||
n |
|
|
|
|
|
n |
|
|
n -1 |
|
|
||||||||
|
|
|
-1 i=1 |
|
|
|
|
|
i=1 |
|
|
||||||||
Исправленное среднее квадратическое отклонение будет иметь вид: |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
å(xi - xв )2 ×ni |
|
|
|
|||
|
|
|
|
|
|
|
|
S = |
|
i=1 |
|
|
|
|
|
|
|||
При большом n |
|
|
|
|
|
|
|
|
n -1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
эти |
|
величины |
примерно |
одинаковы. На практике |
|||||||||||||||
пользуются исправленными дисперсиями и среднеквадратическими
отклонениями, если n < 30 . |
|
|
|||
Пример: |
Из генеральной совокупности извлечена выборка объема n 50 |
||||
|
|
|
|
|
|
xi |
1 |
5 |
7 |
10 |
|
ni |
16 |
12 |
8 |
14 |
|
Найти несмещенную оценку генеральной совокупности.
Решение: Несмещенной оценкой генеральной средней является выборочная средняя
85
xв |
xini 16 2 12 5 8 7 14 10 |
5,76 |
|
|
n |
50 |
|
86

Лекция 17
Интервальные оценки неизвестных параметров. Довери-
тельный интервал, доверительная вероятность. Доверительный интервал для оценки математического ожидания нормального распределения при известном и неизвестном σ . Доверительный интервал для оценки среднеквадратиче-
ского отклонения нормального распределения.
Мы рассматривали точечные оценки, которые определяются одним числом. Точечной оценкой xГ является xв , Dв – точечная оценка DГ .
Доверительный интервал, доверительная вероятность.
Если выборка небольшая, то точечная оценка может значительно отличаться от оцениваемого параметра. По этой причине при небольшом объёме выборки следует пользоваться интервальной оценкой, которая определяется двумя числами – концами интервалов.
Пусть θ * - точечная оценка неизвестного параметра θ (это может
быть выборочное среднее, выборочная дисперсия |
или выборочное среднее |
|||
квадратическое отклонение). Чем меньше разность |
|
θ *−θ |
|
, тем точнее оцен- |
|
|
|||
ка. Если θ *−θ < δ , то δ называется точностью оценки. Статистические методы не позволяют категорически утверждать, что выполняется неравенст-
во |
|
θ *−θ |
|
< δ , |
поэтому |
говорят о вероятности такого |
события: |
||||||||||||
|
|
||||||||||||||||||
P ( |
|
|
θ *−θ |
|
< δ ). |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Определение: Надёжностью (доверительной вероятностью) γ |
называет- |
||||||||||||||||||
ся вероятность неравенства |
|
θ *−θ |
|
< δ , где δ - точность оценки. |
|
||||||||||||||
|
|
|
|||||||||||||||||
Обычно надёжность задаётся наперёд γ = 0,95;0,99;K. |
|
||||||||||||||||||
P ( |
|
θ *−θ |
|
< δ ) = γ ; |
γ =0,999; |
|
|
в ,σв ) ; θ |
|
||||||||||
|
|
|
θ * – точечная оценка (xв , D |
- оцени- |
|||||||||||||||
ваемый параметр. Запишем данную вероятность в виде |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
P(−δ < θ −θ* < δ ) = P(θ *−δ < θ < θ *+δ ) = γ |
|
||||||||
В данном случае говорят, что вероятность того, что интервал (θ *−δ ,θ *+δ ) покрывает оцениваемый параметр θ равна γ .
86
Определение: |
Доверительным интервалом называется интервал |
(θ *-δ ,θ *+δ ) |
который покрывает оцениваемый параметр θ с надёжностью |
γ . |
|
Доверительный интервал для оценки математического ожидания нормального распределения при известном σ .
Пусть количественный признак X генеральной совокупности распределён нормально, причём среднее квадратичное отклонение σ известно.
Требуется оценить неизвестный параметр a по выборочной средней xв . Поставим задачу - найти доверительный интервал, который покрывает
неизвестный параметр a с заданной надёжностью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xв -δ , xв +δ ), δ - ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Будем считать |
xв случайной величиной, зависящей от выборки. Обо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= xв . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
значим эту случайную величину X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Примем без доказательства, |
|
|
|
|
|
|
|
распределена также нормально, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
что X |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
как и X , и их математические ожидания равны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
) = Dæ |
x1 +...+ xn |
ö = |
|
1 |
|
|
|
(D(x ) +...+ D(x |
|
)) = |
|
nD(X ) |
= |
|
|
D(X ) |
|
||||||||||||||||||||||||||||||||||||||||||
D(X |
|
|
n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ç |
|
|
n |
|
÷ |
|
n |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
n |
||||||||||||||||
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) = |
|
|
D(X ) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ (X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для нормального распределения величины X справедлива формула: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
æ |
|
|
|
|
|
δ |
ö |
|
|
|
æ |
δ × |
|
|
ö |
|
|
|
|
|
|
δ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
< δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
||||||||||||||||||||||||||||||
|
|
P |
X - a |
= 2F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2Fç |
|
|
|
|
|
|
÷ |
, t |
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
÷ |
|
|
|
ç |
|
|
|
σ |
|
÷ |
|
|
|
|
|
|
|
σ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
σ (X ) ø |
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
P (-δ < X |
- a < δ ) = 2F(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
P (-X -δ < -a < -X |
+δ ) = 2F(t) |
|
|
|
t = δ |
|
|
|
,δ = |
σt |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+δ ) = 2F(t), |
где |
|
|
n |
|||||||||||||||||||||||||||||||||||||||||
|
|
P(X |
-δ < a < X |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Таким образом, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
n |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P |
æ x - |
σ |
t |
|
|
|
< a < x + |
σ |
t |
|
ö = γ |
, |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
в |
|
|
n |
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
где t |
определяется из равенства: F(t) = |
γ . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

xв - выборочное среднее, a – неизвестное математическое ожидание, n - объём выборки, γ – надёжность.
Пример1: Случайная величина X имеет нормальное распределение, σ = 3. Найти доверительный интервал для оценки неизвестного математического ожидания a по выборочным средним xв = 4,1; n = 36; γ = 0,95; .
Решение: |
|
|
|
|
|
|
|
|||
P æ x - |
tσ |
< a < x + |
tσ |
ö |
= γ |
|||||
|
|
|
||||||||
ç в |
n |
|
в |
÷ |
|
|||||
è |
|
|
|
|
|
|
n ø |
|
||
F(t) = γ |
= 0,475; t = 1,96; |
|
||||||||
2 |
|
|
|
|
|
|
|
|
||
4,1- |
1,96×3 |
< a < 4,1+ |
1,96×3 |
|||||||
|
|
6 |
||||||||
6 |
|
|
|
|
||||||
Получаем доверительный интервал
3,12 < a < 5,08
Пример2: Найти минимальный объем выборки, при котором с надежностью 0,975 точность оценки математического ожидания a генеральной совокупности по выборочной средней будет равна δ = 0,3 , если известно среднее квадратическое отклонение σ = 1,2 нормально распределенной генеральной совокупности.
Решение: Воспользуемся формулой, определяющей точность оценки математического ожидания генеральной совокупности по выборочной средней:
δ = t σn
Отсюда имеем:
n = |
t2σ 2 |
(*) |
|
δ 2 |
|||
|
|
По условию γ = 0,975 или 2F(t ) = 0,975 . Следовательно F(t) = 0,4875 . По таблице найдем t = 2,24 . Подставив t = 2, 24, σ = 1, 2 иδ = 0,2 в формулу (*), получим искомый объем выборки n = 81.
Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном σ .
Можно показать, что доверительный интервал для оценки математического ожидания при неизвестном σ будет определяться по формуле
88

|
|
x - |
tγ |
S |
< a < x + |
tγ |
S |
|
; |
||||||
|
|
|
|
|
|
||||||||||
|
|
в |
|
|
n |
|
в |
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
где S = |
|
n |
|
D |
||||||||
|
|
|
n |
-1 |
|||||||||||
|
|
|
|
|
|
|
|
в |
|||||||
γ - |
надёжность, S - исправленное среднеквадратичное отклонение, |
||||||||||||||
функция tγ |
= tγ (n,γ ) ищется по таблице. |
|
|
|
|
|
|
|
|||||||
Пример: Количественный признак X генеральной совокупности распределён нормально. По выборке объёма n = 16 найдена дисперсия
Dв = 0,6 (S = 0,8) . Оценить неизвестное математическое ожидание с надёжностью 0,95
Решение: По формуле оценки математического ожидания при неиз-
вестном σ |
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
tγ |
× S |
|
|
tγ × S |
|
|
|
|
|
|
|
|
|
|
|||||
x - |
< a < x |
+ |
; |
t |
= t (16,0,95) = 2,13; S = |
n |
|
D = 0,8 |
||||||||||||
|
|
|
|
|
|
n -1 |
||||||||||||||
в |
n |
в |
|
|
n |
γ |
|
γ |
|
|
|
|
в |
|||||||
|
|
|
|
20,2 - |
2,13×0,8 |
|
< a < 20,2 + |
2,13×0,8 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
20,2 - 0,462 < a < 20,2 + 0,426 |
|
|
|
|
||||||||||||
|
|
|
|
19,774 < a < 20,626 |
|
|
|
|
||||||||||||
Оценка истинного значения измеряемой величины. |
||||||||||||||||||||
Пусть произведено n |
независимых измерений некоторой физической |
|||||||||||||||||||
величины, |
истинное значение a |
которой неизвестно. Будем рассматривать |
||||||||||||||||||
результаты отдельных измерений, |
как случайные величины |
X1 , X2 ,..., Xn . |
||||||||||||||||||
Эти величины независимы, имеют одно и то же математическое ожидание a
(истинное значение измеряемой величины), одинаковые дисперсии σ 2 (измерения равноточны) и распределены нормально (что подтверждается опытом). Поэтому можем воспользоваться формулами для доверительных интервалов. Так как σ обычно неизвестно, то, как правило, пользуются формулой:
|
|
tγ × S |
|
|
tγ × S |
|
|
|
X1 + X2 +...+ Xn |
|
|
|
|
|||||||||
|
|
- |
|
|
+ |
; где |
|
|
|
; S = |
n |
D |
||||||||||
X |
< a < X |
X |
= |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
n |
n -1 |
в |
||||||
Доверительный интервал для оценки среднеквадратического отклонения нормального распределения.
89
