3. Число е

Розглянемо послідовність з загальним членом . Покажемо, що ця послідовність є збіжною. Для цього спочатку установимо, що вона зростаюча, а потім – що вона обмежена.

Згідно формули бінома Ньютона

Подамо цей вираз у наступному вигляді

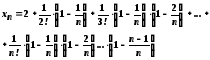(3)

Так само одержуємо

.

При 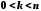виконується нерівність, тому, тобто послідовність зростаюча.

Оскільки кожний вираз, який стоїть у дужках у формулі (3) менший від одиниці і 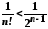при, то

.

За формулою суми нескінченно спадної геометричної прогресії маємо

.

Отже, послідовність обмежена. Таким чином, послідовність із загальним членом 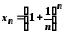збіжна. За означенням границю цієї послідовності позначають буквою, тобто

.

Лекція 7

7. Теорема про вкладені відрізки.

8. Підпослідовність числової послідовності.

9. Теорема Больцано - Вейєрштрасса.

10. Критерій Коші збіжності числової послідовності. Фундамкнтальна послідовність.

1. Теорема про вкладені відрізки

Нехай задана послідовність відрізків

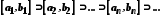, де (4)

для всіх , таких, що кожний наступний міститься в попередньому і при зростаннідовжина-ного відрізка прямує до нуля, тобто. Таку послідовність називатимемо послідовністю вкладених відрізків.

Теорема. Для будь-якої послідовності вкладених відрізків існує єдина точка, яка належить усім відрізкам даної послідовності.

Доведення. З означення вкладених відрізків випливає, що їх ліві кінці утворюють неспадну послідовність

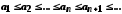, (5)

а праві – незростаючу

. (6)

При цьому послідовність (5) обмежена зверху, а послідовність (6) обмежена знизу, оскільки 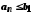і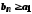. Отже, ці послідовності мають границі. Нехай. За умовою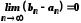, а тому

.

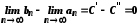Отже, . Покладемо. Тоді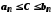для всіх, тобто точка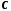належить усім відрізкам (4).

Покажемо, що така точка єдина. Припустимо, що існує точка 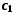, відмінна від точкиі така, що належить усім відрізкам (4). Тоді для будь-якогоповинна виконуватися нерівність, з якої випливає , що, що суперечить умові.

Зазначимо, що теорема не справджується, якщо замість відрізків розглядати інтервали 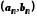, наприклад для послідовності вкладених інтервалів

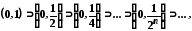(6)

яку б точку 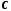з інтервалуне взяти, вона не буде належати всім інтервалам (6).

2. Підпослідовність числової послідовності

Нехай задана деяка послідовність . Розглянемо довільну зростаючу послідовність натуральних чисел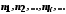. Виберемо з послідовності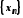елементи з номерами, і розмістимо їх в тому самому порядкові, що і числа.

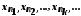Одержана числова послідовність називається підпослідовністю послідовності 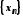. Можна встановити, що коли послідовністьзбіжна і має границею число, то будь-яка її підпослідовність також збіжна й має границею число.

3. Теорема Больцано-Вейєрштрасса

Теорема. Із будь-якої обмеженої послідовності 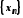можна виділити збіжну підпослідовність.

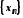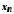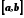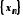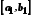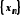Доведення. Нехай послідовність обмежена, тобто існує такий відрізок, що для всіхвиконується нерівність. Поділимо відрізокпополам. Тоді принаймні в одній половині буде міститися нескінченна множина елементів послідовності. Позначимо цю половину. Поділимо тепер відрізокна два рівних відрізки і знову виберемо той із них, у якому міститься нескінченна множина елементів послідовності. Позначимо його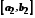. Продовжуючи цей процес, дістанемо послідовність укладених відрізків

,

у яких довжина -го відрізкапрямує до нуля при . Отже, за теоремою про вкладені відрізки.

Побудову підпослідовності послідовності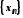виконаємо так: у значенні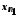виберемо довільний елемент із, який належить відрізку, у значенні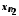- довільний елемент із , котрий належить відрізку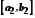і т. д. Оскільки для вибраних таким чином елементів виконується нерівність, то за теоремою 2.7.