
- •Лекція 5
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази. Теорема Штольца
- •Лекція 6
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •Лекція 7
- •1. Теорема про вкладені відрізки
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності. Фундаментальна послідовність
- •Лекція 8
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Питання для самостійного опрацювання
- •Функції однієї змінної
- •2. Класифікація функцій
- •3. Елементарні функції.
- •Тема 3. Границя функції однієї змінної лекція 9
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •Лекція 10
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
Лекція 10
Визначні границі.
Нескінченно малі й нескінченно великі функції.
Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
1. Визначні границі
Перша визначна
границя . Покажемо,
що
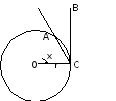
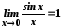 .
.
Розглянемо у крузі
радіуса
 гострий кут
гострий кут ,
хорду
,
хорду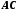 і дотичну до кола в точці
і дотичну до кола в точці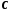 (рис.
4). Для площ трикутників
(рис.
4). Для площ трикутників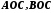 та колового сектора
та колового сектора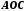 виконуються нерівності
виконуються нерівності
Рис. 4
 .
.
Отже,
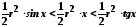 .
.
Звідси
 .
.
Розділивши ці
нерівності на
 (
(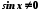 ,
оскільки
,
оскільки ),
одержимо
),
одержимо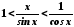 .
Із останніх нерівностей випливає
.
Із останніх нерівностей випливає
 .
.
Помноживши всі частини на (–1) та додавши 1, матимемо
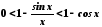 .
.
Оскільки
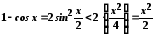 ,
то
,
то .
.
Задамо довільне
число
 > 0.
Нерівність
> 0.
Нерівність
 або
або

справджується, як
тільки
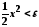 ,
тобто
,
тобто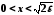 .
Таким чином, для довільного числа
.
Таким чином, для довільного числа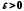 існує число
існує число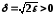 таке, що для всіх
таке, що для всіх ,
які задовольняють умову
,
які задовольняють умову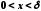 ,
виконується нерівність
,
виконується нерівність
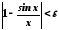 .
.
Із цього випливає,
що 1 є правою границею функції
 ,
тобто
,
тобто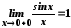 .
Оскільки функція
.
Оскільки функція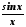 парна, то і
парна, то і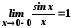 .
Отже,
.
Отже,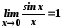 .
.
Друга визначна границя. Доведемо, що
 .
.
Раніше було
встановлено, що
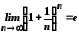 .
Нехай
.
Нехай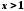 .
Покладемо
.
Покладемо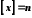 .
Тоді
.
Тоді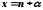 ,
де
,
де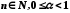 .
Оскільки
.
Оскільки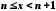 ,
то
,
то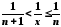 .
Отже,
.
Отже,
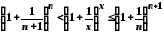 .
(6)
.
(6)
Якщо
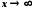 ,
то і
,
то і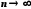 .
При цьому
.
При цьому
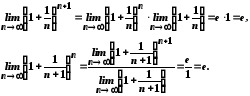
Ураховуючи співвідношення (6), маємо
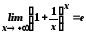 .
.
Нехай тепер
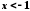 .
Покладемо
.
Покладемо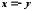 .
Тоді
.
Тоді
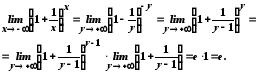
Ураховуючи обидва випадки, одержуємо
 .
.
2. Нескінченно малі й нескінченно великі функції
Нескінченно
малі функції.
Функція
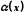 називається нескінченно малою в точці
називається нескінченно малою в точці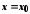 (
або при
(
або при
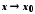 ),
якщо
),
якщо
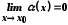 .
.
Аналогічно
означаються нескінченно
малі функції при
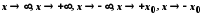 .
.
Виходячи з означень границі функції за Гейне і за Коші, можна навести наступні рівносильні означення нескінченно малої функції.
Функція
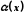 називається нескінченно малою в точці
називається нескінченно малою в точці
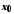 ,
якщо для будь-якої збіжної до
,
якщо для будь-якої збіжної до
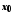 послідовності
послідовності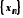 значень аргументу
значень аргументу ,
відмінних від
,
відмінних від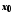 ,
відповідна послідовність
,
відповідна послідовність
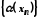 єнескінченно
малою.
єнескінченно
малою.
Функція
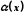 називається нескінченно малою в точці
називається нескінченно малою в точці
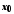 ,
якщо для
довільного числа
,
якщо для
довільного числа
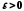 існує число
існує число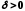 таке, що нерівність
таке, що нерівність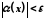 виконується для всіх
виконується для всіх ,
які задовольняють умову
,
які задовольняють умову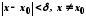 .
.
Теорема
. Число
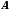 є границею функції
є границею функції у точці
у точці
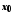 тоді і тільки тоді, коли
тоді і тільки тоді, коли
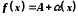 ,
де
,
де
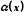 – нескінченно мала функція в точці
– нескінченно мала функція в точці
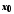 .
.
Доведення.
Нехай
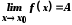 .
Покажемо, що різниця
.
Покажемо, що різниця
 є нескінченно
малою в точці
є нескінченно
малою в точці
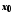 .
Дійсно,
.
Дійсно,
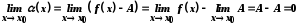 .
.
Нехай тепер
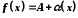 ,
де
,
де
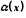 – нескінченно мала функція в точці
– нескінченно мала функція в точці
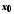 .
Тоді
.
Тоді
 .
.
Нескінченно малі функції мають такі ж властивості, як і нескінченно малі послідовності:
алгебраїчна сума
скінченного числа нескінченно малих у
точці
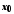 функцій є нескінченно малою в точці
функцій є нескінченно малою в точці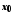 функцією;
функцією;
добуток скінченного
числа нескінченно малих у точці
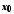 функцій, а також добуток нескінченно
малої функції на обмежену функцію є
нескінченно малою в точці
функцій, а також добуток нескінченно
малої функції на обмежену функцію є
нескінченно малою в точці функцією.
функцією.
Викладене
вище має місце також для нескінченно
малих функцій функції при
 .
.
Нескінченно
великі функції.
Нехай функція
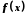 визначена в деякому околі точки
визначена в деякому околі точки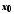 .
.
Функція
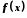 називається нескінченно великою в точці
називається нескінченно великою в точці
 ,
якщо для будь-якого числа
,
якщо для будь-якого числа
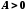 існує число
існує число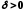 таке, що для всіх
таке, що для всіх ,
які задовольняють умову
,
які задовольняють умову ,
виконується нерівність
,
виконується нерівність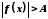 .
.
Означення
нескінченно великої в точці
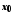 функції можна дати мовою послідовностей.
функції можна дати мовою послідовностей.
Функція
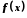 називається нескінченно великою в точці
називається нескінченно великою в точці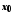 ,
якщо для будь-якої збіжної до
,
якщо для будь-якої збіжної до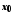 послідовності
послідовності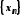 ,
,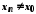 відповідна послідовність
відповідна послідовність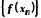 значень функції є нескінченно великою.
значень функції є нескінченно великою.
Символічно
це записують так:
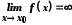 і говорять, що функція
і говорять, що функція у точці
у точці
 має нескінченну границю.
має нескінченну границю.
Якщо
при

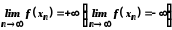 ,
то пишуть
,
то пишуть
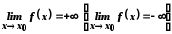 .
.
Аналогічно означенням границі на нескінченності та скінченних односторонніх границь означаються нескінченні границі. При цьому використовуються відповідні записи, наприклад:
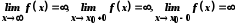 .
.
Теорема.
Якщо
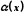 нескінченно мала в точці
нескінченно мала в точці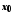 функція, причому в околі точки
функція, причому в околі точки
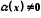 ,
то
функція
,
то
функція
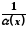 у точці
у точці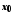 − нескінченно велика. І навпаки, якщо
функція
− нескінченно велика. І навпаки, якщо
функція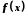 − нескінченно велика в точці
− нескінченно велика в точці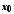 ,
то функція
,
то функція у точці
у точці − нескінченно мала.
− нескінченно мала.
Дана теорема легко доводиться мовою послідовностей.
