
- •Лекція 5
- •1. Збіжні послідовності
- •2. Властивості збіжних послідовностей
- •3. Невизначені вирази. Теорема Штольца
- •Лекція 6
- •1. Граничний перехід у нерівностях
- •2. Монотонні послідовності
- •3. Число е
- •Лекція 7
- •1. Теорема про вкладені відрізки
- •3. Теорема Больцано-Вейєрштрасса
- •4. Критерій Коші збіжності числової послідовності. Фундаментальна послідовність
- •Лекція 8
- •1. Поняття метричного простору
- •2. Повні метричні простори.
- •3. Доповнення простору.
- •Питання для самостійного опрацювання
- •Функції однієї змінної
- •2. Класифікація функцій
- •3. Елементарні функції.
- •Тема 3. Границя функції однієї змінної лекція 9
- •1. Границя функції. Означення границі функції за Гейне й за Коші.
- •2. Односторонні границі
- •3. Границя функції на нескінченності
- •4.Теореми про границі функцій
- •Лекція 10
- •1. Визначні границі
- •2. Нескінченно малі й нескінченно великі функції
- •3. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
2. Повні метричні простори.
Послідовність
 точок
метричного простору називається
фундаментальною, якщо вона задовольняє
критерій Коші, тобто якщо
точок
метричного простору називається
фундаментальною, якщо вона задовольняє
критерій Коші, тобто якщо
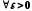
 таке, що
таке, що
 .
.
Якщо в просторі
 будь-яка фундаментальна послідовність
збігається, то цей простір називається
повним.
будь-яка фундаментальна послідовність
збігається, то цей простір називається
повним.
Простір
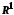 дійсних чисел є повним.
дійсних чисел є повним.
Щоб метричний
простір
 був повним, необхідно і достатньо, щоб
у ньому будь-яка послідовність укладених
одна в одну замкнутих куль, радіуси
котрих прямують до нуля, мала непорожній
переріз.
був повним, необхідно і достатньо, щоб
у ньому будь-яка послідовність укладених
одна в одну замкнутих куль, радіуси
котрих прямують до нуля, мала непорожній
переріз.
Теорема Бера. Повний метричний простір не можна подати у вигляді об'єднання зліченного числа ніде не щільних множин.
Із теореми Бера зокрема випливає, що всякий повний метричний простір без ізольованих точок незліченний.
3. Доповнення простору.
Якщо простір
 не повний, то його завжди можна включити
єдиним способом у повний простір.
не повний, то його завжди можна включити
єдиним способом у повний простір.
Простір
 називається доповненням метричного
простору
називається доповненням метричного
простору![]() ,
якщо:
,
якщо:
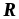 є підпростором
простору
є підпростором
простору
 ;
;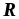 скрізь щільний у
скрізь щільний у
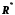 ,
тобто
,
тобто .
.
Простір
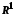 усіх дійсних чисел є доповненням простору
усіх дійсних чисел є доповненням простору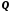 раціональних чисел.
раціональних чисел.
Питання для самостійного опрацювання
1.Функції однієї змінної.
2. Класифікація функцій.
3. Елементарні функції.
Функції однієї змінної
Задання функції однієї змінної. Раніше ми розглянули загальне поняття відображення або функції. Далі ми перейдемо до більш повного дослідження функцій однієї змінної.
Перш за все зазначимо, що існують три основні способи задання функції: аналітичний, табличний, графічний.
При аналітичному способі задання функції закон відповідності між аргументом і функцією подається у вигляді формули ( аналітичного виразу), де дії потрібно виконати над значеннями аргументу та сталими числами, щоб одержати значення функції, відповідне даному аргументу.
Приклади.
1. Формула
 задає функцію, областю визначення якої
є числова пряма
задає функцію, областю визначення якої
є числова пряма ,
а множиною значень – півпряма
,
а множиною значень – півпряма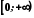 .
Графіком цієї функції є парабола (рис.
1).
.
Графіком цієї функції є парабола (рис.
1).
Формула
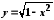 задає функцію, областю визначення якої
є відрізок
задає функцію, областю визначення якої
є відрізок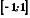 ,
а множиною значень – відрізок
,
а множиною значень – відрізок (рис. 2).
(рис. 2).Функція
 (знак
(знак
 )
задається так:
)
задається так:

Її графік зображено
на рисунку 3. Функція визначена на всій
числовій прямій
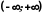 ,
а її множина значень складається з трьох
чисел:
,
а її множина значень складається з трьох
чисел: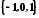 .
.

4. Функція Діріхле
 .
.
Ця функція визначена
на всій числовій прямій
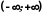 ,
а її множина значень складається з двох
чисел:
,
а її множина значень складається з двох
чисел: .
Зазначимо, що графік функції Діріхле
побудувати неможливо.
.
Зазначимо, що графік функції Діріхле
побудувати неможливо.
При табличному
способі задання функції будується
таблиця, в якій указано, як для кожного
значення аргументу
 знаходити відповідне значення функції.
знаходити відповідне значення функції.
Графічний спосіб
задання функції використовується у
практиці фізичних вимірювань, коли
відповідність між змінними
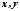 задається графіком. У багатьох випадках
такі графіки будуються за допомогою
різних самописних приладів, таких, як
барограф, осцилограф, електрокардіограф
та ін. Криві, що їх виписують прилади,
задають цілком певну функцію, властивості
якої треба знати для вивчення того чи
іншого процесу.
задається графіком. У багатьох випадках
такі графіки будуються за допомогою
різних самописних приладів, таких, як
барограф, осцилограф, електрокардіограф
та ін. Криві, що їх виписують прилади,
задають цілком певну функцію, властивості
якої треба знати для вивчення того чи
іншого процесу.
2. Класифікація функцій
Обмежені функції.
Функція на множині
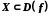 називається
називається
обмеженою знизу, якщо існує число
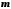 таке, що для всіх
таке, що для всіх виконується нерівність
виконується нерівність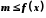 ;
;обмеженою зверху, якщо існує число
 таке, що для всіх
таке, що для всіх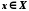 виконується нерівність
виконується нерівність ;
;обмеженою, якщо існує число
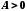 таке, що для всіх
таке, що для всіх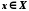 виконується нерівність
виконується нерівність .
.
Говорячи про
обмеженість функції, ми тим самим
характеризуємо множину
 її значень. Отже, до цієї множини
застосовні ті поняття, які було викладено
при розгляді питання " Межі числових
множин".
її значень. Отже, до цієї множини
застосовні ті поняття, які було викладено
при розгляді питання " Межі числових
множин".
Монотонні
функції.
Функція
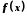 на множині
на множині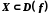 називається
називається
зростаючою, якщо меншому значенню аргументу (
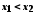 )
відповідає менше значення функції
)
відповідає менше значення функції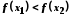 ;
;
спадною, якщо при виконанні нерівності
 виконується нерівність
виконується нерівність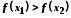 ;
;неспадною, якщо при виконанні нерівності
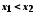 справедлива нерівність
справедлива нерівність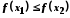 ;
;незростаючою, якщо виконання нерівності
 тягне за собою виконання нерівності
тягне за собою виконання нерівності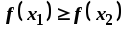 .
.
У вказаних
означеннях мається на увазі, що
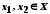 .
.
Названі вище функції називаються монотонними. Зростаючі і спадні функції називаються строго монотонними.
Парні
та непарні функції.
Нехай область визначення
 функції
функції![]() симетрична відносно початку координат.
Тоді функція
симетрична відносно початку координат.
Тоді функція![]() називається
називається
парною, якщо
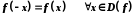 ;
;непарною, якщо
 .
.
Графік парної
функції симетричний відносно осі
 ,
а непарної – відносно початку координат.
,
а непарної – відносно початку координат.
Теорема.
Будь-яку функцію, визначену на множині
 ,
симетричній відносно початку координат,
можна єдиним способом подати у вигляді
суми парної та непарної функції.
,
симетричній відносно початку координат,
можна єдиним способом подати у вигляді
суми парної та непарної функції.
Доведення.
Нехай функція
![]() визначена на множині
визначена на множині ,
симетричній відносно початку координат.
Тоді
,
симетричній відносно початку координат.
Тоді
 .
.
Позначимо
 .
.
Тоді

Покажемо, що дане
подання функції
![]() у вигляді суми парної та непарної єдине.
у вигляді суми парної та непарної єдине.
Нехай

Тоді
 .
.
Отже,

Таким чином,
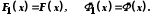
Періодичні
функції.
Функція
 ,
визначена на всій числовій прямій
,
визначена на всій числовій прямій ,
називається періодичною, якщо існує
число
,
називається періодичною, якщо існує
число таке, що
таке, що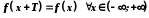 .
.
Число
 називається періодом функції
називається періодом функції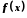 .
Якщо
.
Якщо − період функції, то і число
− період функції, то і число ,
де
,
де також період функції, тобто періодична
функція має нескінченну множину періодів,
найменший додатний період періодичної
функції
також період функції, тобто періодична
функція має нескінченну множину періодів,
найменший додатний період періодичної
функції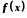 називається основним періодом або
просто періодом.
називається основним періодом або
просто періодом.
Серед періодичних функцій значне місце займають функції
 (1)
(1)
які описують рухи,
що називаються гармонійними коливаннями.
У формулі (1) число
 називається амплітудою коливання,
називається амплітудою коливання, – циклічною частотою,
– циклічною частотою, –
початковою
фазою. Основний період функції
–
початковою
фазою. Основний період функції
 .
Самі функції виду (1) називаються
гармонійними.
.
Самі функції виду (1) називаються
гармонійними.
