Приклад
Нехай –180о≤ θz≤ 180о; –60о≤ θу1≤ 240о; Схзд = 1м; Сузд = 1м; Сzзд = 0,817м.
Тоді: θz≤ 45о або –135о; θу1= 30о або 210о (θz= 45о), 150о або –30о (θz= –135о), ℓх2 = ±0,817/0,5 = ±1,634 м.
Розв’язок ℓх2 < 0 відкидається через абсурдність. Але неоднозначність розв’язку зберігається – є два правильних шляхи розв’язання (рис.2), один з котрих характеризується меншим кутом повороту першої координати (θz = 45o) і є оптимальним. При збільшенні числа ступенів рухливості маніпулятора, якщо рівняння зв’язку мають аналітичні розв’язання, зростає число допустимих розв’язків і вибір оптимальних з них може бути складнішим, ніж у розглянутому випадкові.
Гj4зд = Гj4(q).
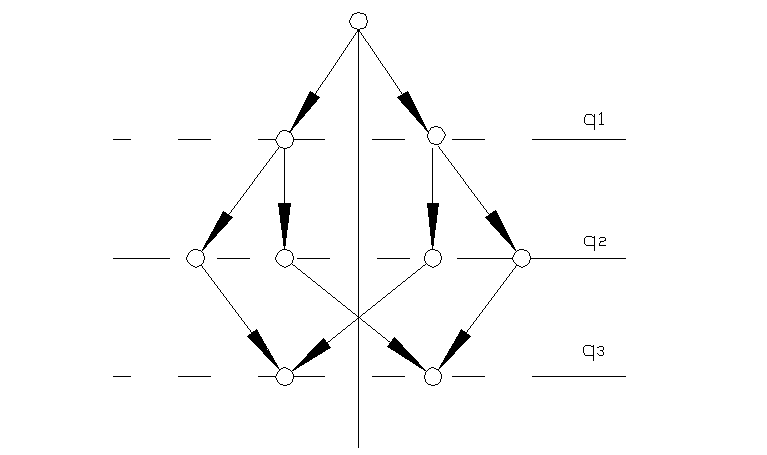
Рис.7.2. Граф вибору допустимих розв’язань зворотної задачі кінематики маніпулятора.
Наближені методи
Наближені методи дозволяють розв’язати зворотну задачу для будь-якої кінематичної схеми маніпулятора. Вона зводиться до численних розв’язань рівняння зв’язку Хізд = Хі(q).
Зворотна задача може розв’язуватися шляхом мінімізації функціоналу розузгодження:
І2(Q) = |Хзд – Х(Q)|2,
де Хзд – вектор положення у системі координат 00x0y0z0;
Х(Q) – вектор положення в узагальнених координатах, що функціонально залежить від вектора узагальнених координат Q= [q1,q2,…qi]T, і = 1,2,3,…n.
Мінімізація цього виразу, як правило, проводиться градієнтним методом із кінцевим кроком. Для цього треба у векторному просторі допустимих значень узагальнених координат Q вибрати можливі напрямок і крок зміни вектора Q при дотриманні умови Q € Q і побудувати послідовність Q[0], Q[1], …,Q[k], … Q[m], яка є мінімізуючою для функціоналі I2(Q), тобто
I2(Q[0]) > І2(Q[1]) >…> І2(Q[k]) > І2(Q[m]).
Процедура отримання цього виразу полягає, по-перше, із визначення координат вектора градієнта ∂I2(Q[0])∂qі і = 1,2,…,n.
Далі на першому кроці ітерації qi[0], і = 1,2,…n вибирають такі напрямки Δqi[1], щоб отримати переважно від’ємні значення вектора градієнта.
Потім на кожному кроку ітерації дають приріст Δqi[k], знаходять величину І2(Qi[k]) і перевіряють виконання послідовності. По мірі зменшення модуля градієнта зменшують величину кроку Δqi[k].
При неможливості або непрактичності визначення градієнта функціоналу переходять до кінцевих різниць ΔІ2(Q)/ Δqi. Почергово змінюють кожну координату та один крок ітерації виконується за nкроків.
Метод Ньютона
Широке застосування дістав метод Ньютона, згідно з котрим нелінійне рівняння зв’язку представляють у лінійному наближенні. Знаючи початкове значення координат qi[j], на кожному j–тому кроці ітераційного процесу шляхом розв’язання лінійних рівнязання знаходять наступне значення координат qi[j+1], що використовують як початкове для (j+1) - го кроку.
Лінійне наближення рівнянь зв’язку має вигляд
(7.4)
Знову звернемося до прикладу
маніпулятора з полярною циліндричною
системою
.
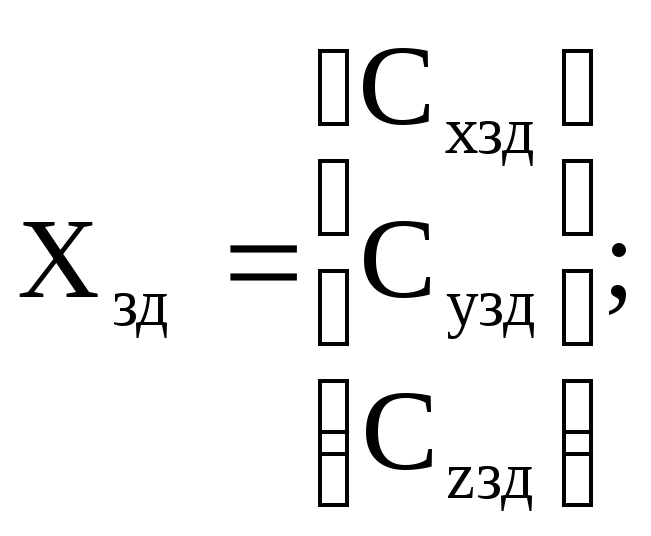
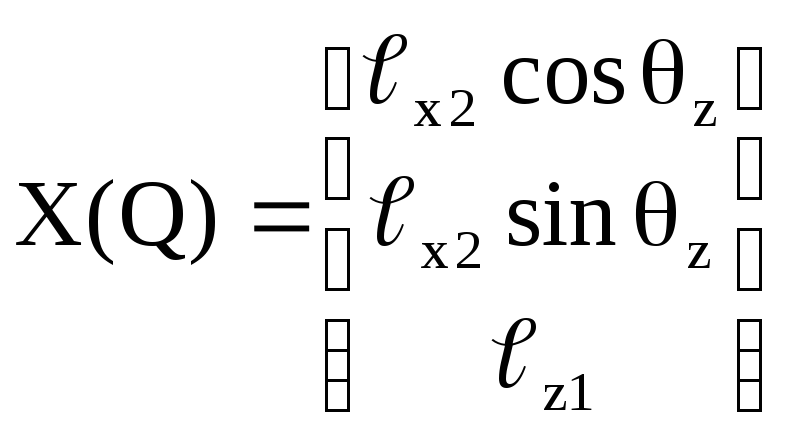(7.5)
координат при тих же початкових
умовах і заданому кінцевому положенні
захвату, з тією тільки різницею, що для
зручності запису рівнянь проведемо
заміну першої координати, прийнявшиq1 = sinθz,
тобто q1[0]
= sin θz
= 0,707.
У лінійному наближенні рівняння зв’язку для цього маніпулятора мають вигляд
Розв’яжемо це рівняння відносно qi[j+1] i q3[j+1] (q2 = const).
Перші два рівняння системи перетворимо до такого вигляду:
sinθz[j+1] = sinθz[j] – Cxзад/(ℓх2[j]tgθz[j]) + cos θz[j]ℓx2[j+1]/(ℓх2[j]tgθz[j]),
ℓх2[j+1] = Сузд/sinθz[j] – ℓх2[j]sinθz[j+1]/sin θz[j] + ℓх2[j].
Якщо ввести позначення:
А[j]=Cузд/sinθz[j]+ ℓx2[j],
B[j]= ℓx2[j]/sinθz[j],
C[j]=sinθz[j]–Cxзд/(ℓх2[j]tgθz[j]),
D[j]=cosθz[j]/ (ℓх2[j]tgθz[j]),
то загальний розв’язок цих співвідношень дає наступні вирази:
q3[j+1] = ℓx2[j+1] = (A[j] – B[j]C[j])/(1+B[j]D[j]),
q1[j+1] = sinθz[j+1] = C[j] + D[j]ℓх2[j+1].