§7. Квадратичные формы.

Определение:Однородный многочлен второй степени относительно переменныхх₁ их₂

Ф(х₁, х₂) = а₁₁,

не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формойпеременныхх₁их₂.

Определение:Однородный многочлен второй степени относительно переменныхх₁,х₂их₃

не содержащий свободного члена и неизвестных в первой степени называется квадратичной формойпеременныхх₁,х₂их₃.

Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А =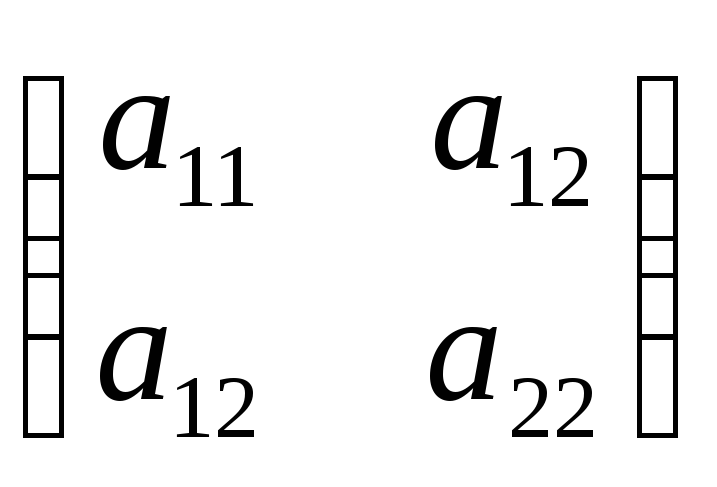. Определитель этой матрицы называетсяопределителем квадратичной формы.

Пусть на плоскости задан ортогональный базис . Каждая точка плоскости имеет в этом базисе координаты х₁, х₂.

Если задана квадратичная форма Ф(х₁, х₂) = а₁₁, то ее можно рассматривать как функцию от переменных х₁и х₂.

Приведение квадратичных форм к каноническому виду.

Рассмотрим некоторое линейное преобразование А с матрицей .

Это симметрическое преобразование можно записать в виде:

y₁ = a₁₁x₁ + a₁₂x₂

y₂ = a₁₂x₁ + a₂₂x₂

где у₁и у₂– координаты векторав базисе.

Очевидно, что квадратичная форма может быть записана в виде

Ф(х₁, х₂) = х₁у₁+ х₂у₂.

Как видно, геометрический смысл числового значения квадратичной формы Ф в точке с координатами х₁и х₂– скалярное произведение.

Если взять другой ортонормированный базис на плоскости, то в нем квадратичная форма Ф будет выглядеть иначе, хотя ее числовое значение в каждой геометрической точке и не изменится. Если найти такой базис, в котором квадратичная форма не будет содержать координат в первой степени, а только координаты в квадрате, то квадратичную форму можно будет привести к каноническому виду.

Если в качестве базиса взять совокупность собственных векторов линейного преобразования, то в этом базисе матрица линейного преобразования имеет вид:

.

При переходе к новому базису от переменных х₁и х₂мы переходим к переменными. Тогда:

Тогда.

Выражениеназываетсяканоническим видомквадратичной формы. Аналогично можно привести к каноническому виду квадратичную форму с большим числом переменных.

Теория квадратичных форм используется для приведения к каноническому виду уравнений кривых и поверхностей второго порядка.

Пример.Привести к каноническому виду квадратичную форму

Ф(х₁, х₂) = 27.

Пример.Привести к каноническому виду уравнение второго порядка:

17x²+ 12xy+ 8y²– 20 = 0.

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение:

Пример. Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

Решение:Составим характеристическое уравнение квадратичной формы: при

Решив это уравнение, получим ₁ = 1,₂ = 11.

Найдем координаты собственных векторов:

полагаяm₁ = 1, получимn₁ =

полагаяm₂ = 1, получимn₂ =

Собственные векторы:

Находим координаты единичных векторов нового базиса.

Имеем следующее уравнение линии в новой системе координат:

Каноническое уравнение линии в новой системе координат будет иметь вид:

Пример.Используя теорию квадратичных форм, привести к каноническому виду уравнение линии второго порядка. Схематично изобразить график.

4ху + 3у²+ 16 = 0

Коэффициенты: a₁₁= 0;a₁₂= 2;a₂₂= 3.

Характеристическое уравнение:

Корни: ₁= -1,₂= 4.

Для ₁= -1 Для₂= 4

m₁= 1;n₁= -0,5;m₂= 1;n₂= 2;

= (1; -0,5) = (1; 2)

Получаем: -каноническое уравнение гиперболы.