5.1.Плоскость в пространстве.
Пусть Р– произвольная плоскость в пространстве.
ТочкаМ0(x0,
y0, z0)
Р. Вектор
= (A,B,C)
–ненулевой вектор, перпендикулярный
плоскостиР(нормальный вектор
плоскости)
Необходимо получить уравнение плоскости.
Решение.
Для произвольной
точки М(х, у, z),принадлежащей плоскости, составим
вектор
.
Т.к. вектор
- вектор нормали, то он перпендикулярен
плоскости, а, следовательно, перпендикулярен
и вектору
.
Тогда скалярное произведение
=
0
Таким образом, получаем уравнение плоскости
(5.1)
Уравнение (5.1) называют уравнением плоскости, проходящей через заданную точку.
Легко показать, что уравнение (5.1) приводится к виду:
Ax + By + Cz + D = 0– уравнение 1-ой степени относительно переменных координатх, у, z (D = -Ax0 – By0 – Cz0).
Определение.Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:
Ax + By + Cz + D = 0,(5.2)
где А, В, С– координаты вектора
-
векторнормалик плоскости.
Рассмотрим особенности расположения плоскости в тех случаях, когда те или иные коэффициенты уравнения (5.2) обращаются в нуль.
Частные случаи общего уравнения плоскости:
D = 0:Ax+By+Cz= 0– уравнение плоскости, проходящей через начало координат
А = 0:By+Cz+D= 0 – уравнение плоскости, параллельной оси ОХ, т.к. нормальный вектор
= (0,B,C) –
перпендикулярен оси ОХ (его проекция
на ось ОХ равна нулю). Аналогично при
В = 0: Ax+Cz+D= 0 – плоскость параллельна оси Оу
С = 0:Ax+By+D= 0– плоскость параллельна оси Оz
А = D = 0:By+Cz= 0 – уравнение плоскости, проходящей через ось Ох, поскольку она параллельна оси Ох (А=0) и проходит через начало координат (D=0). Аналогично при
В = D = 0:Ax+Cz= 0 – плоскость проходит через ось Оу
С = D = 0:Ax+By= 0 – плоскость проходит через осьOz
А = В = 0:Cz+D= 0– уравнение плоскости, параллельной координатной плоскости хОу, поскольку она параллельна осям Ох (А=0) и Оy(В=0). Аналогично:
А = С = 0:By+D= 0 – уравнение плоскости, параллельной координатной плоскости хОz
В = С = 0:Ax+D= 0 – уравнение плоскости, параллельной координатной плоскостиyOz.
А = В = D = 0:Cz= 0 (z= 0 ) – уравнение координатной плоскости хОу, т.к. она параллельна плоскости хОу (А = В = 0) и проходит через начало координат (D=0). Аналогично при
А = С = D = 0: By= 0 (y= 0) – плоскость совпадает с плоскостьюxOz
В = С = D = 0:Ax= 0 (x= 0)– плоскость совпадает с плоскостьюyOz
Уравнение плоскости, проходящей через три точки.
Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1,y1,z1),M2(x2,y2,z2),M3(x3,y3,z3) в общей декартовой системе координат.
Для того,
чтобы произвольная точка М(x,y,z) лежала
в одной плоскости с точками М1,
М2, М3необходимо, чтобы
векторы
были компланарны.
Уравнение плоскости, проходящей через три точки:
(5.3)
Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости.
Пусть заданы точки
М1(x1,y1,z1),M2(x2,y2,z2)
и вектор
.
Составим
уравнение плоскости, проходящей через
данные точки М1и М2и
произвольную точку М(х, у,z)
параллельно вектору
.
Уравнение плоскости:
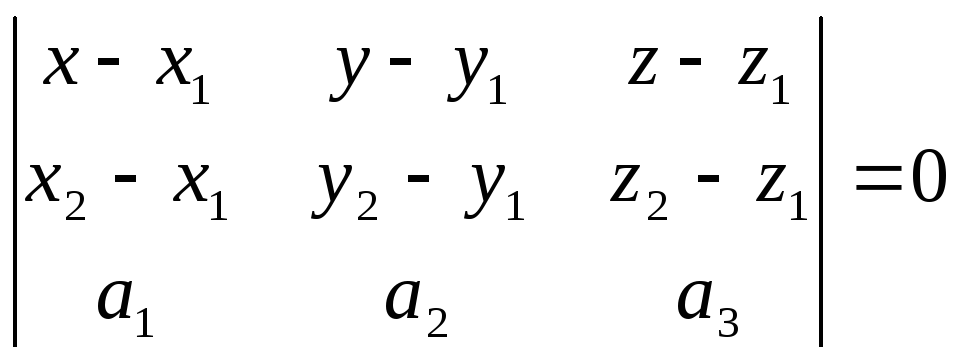(5.4)
Уравнение плоскости по одной точке и двум векторам,
коллинеарным плоскости.
Пусть заданы два
вектора
и
,
коллинеарные плоскости.
Уравнение плоскости:
(5.5)
Уравнение плоскости в отрезках.
Если в общем уравнении Ах + Ву + Сz+D= 0 поделить обе части на (-D)
,
заменив
,
получим уравнение плоскости в отрезках:
(5.6)
Числаa,b,cявляются точками пересечения плоскости соответственно с осями 0х, 0у, 0z.
Уравнение плоскости в векторной форме.
где
-
радиус- вектор текущей точки М(х, у,z),
- единичный вектор, имеющий направление,
перпендикуляра, опущенного на плоскость
из начала координат.
, и- углы, образованные этим вектором с осямих, у, z.
p –длина этого перпендикуляра.
В координатах это уравнение имеет вид:
xcos+ycos+zcos-p= 0.(5.7)
Расстояние от точки до плоскости.
Расстояние
от произвольной точки М0(х0,
у0,z0) до
плоскости Ах+Ву+Сz+D=0
равно:
(5.8)
Пример.Найти уравнение плоскости, проходящей через две точкиP(2; 0; -1) и
Q(1; -1; 3) перпендикулярно плоскости 3х + 2у –z+ 5 = 0.
Пример.Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и
В(3, 2, -1) перпендикулярно плоскости х+у+ 2z– 3 = 0.
Пример.Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.
Пример.Даны координаты вершин пирамиды А1(1; 0; 3),A2(2; -1; 3),A3(2; 1; 1),
A4(1; 2; 5).
Найти длину ребра А1А2.
Найти угол между ребрами А1А2и А1А4.
Найти угол между ребром А1А4и гранью А1А2А3.
Найти площадь грани А1А2А3.
Найти уравнение плоскости А1А2А3.
Воспользуемся формулой уравнения плоскости, проходящей через три точки.
Угол между плоскостями.
1
0
Угол между двумя плоскостями в пространствесвязан с углом между нормалями к этим плоскостям1соотношением:=1или= 1800-1, т.е.
cos=cos1.
Определим угол 1. Известно, что плоскости могут быть заданы соотношениями:
,
где
(A1,B1,C1),
(A2,B2,C2).
Угол между векторами нормали найдем из
их скалярного произведения:
.
Таким образом, угол между плоскостями находится по формуле:
(5.9)
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.