Связь цилиндрической и декартовой прямоугольной

системами координат.

Аналогично полярной системе координат на плоскости можно записать соотношения, связывающие между собой различные системы координат в пространстве. Для цилиндрической и декартовой прямоугольной систем эти соотношения имеют вид:

h = z; x = rcos; y = rsin; cos = ; sin = .

Связь сферической системы координат с

декартовой прямоугольной.

В случае сферической системы координат соотношения имеют вид:

§6. Линейные преобразования.

Определение:Будем считать, что в линейном пространствеLзадано некоторое линейное преобразование А, если любому элементуLпо некоторому правилу ставится в соответствие элемент АL.

Определение:Преобразование А называетсялинейным, если для любых векторовLиLи любоговерно:

A(+) =A+A

A() =A

Определение:Линейное преобразование называетсятождественным, если оно преобразует элемент линейного пространства сам в себя.

Е=

Пример.Является ли А линейным преобразованием. А=+;0.

Запишем преобразование А для какого- либо элемента . А=+

Проверим, выполняется ли правило операции сложения для этого преобразования А(+) =++;A() +A() =+++, что верно только при= 0, т.е. данное преобразование А нелинейное.

Определение:Если в пространствеLимеются векторы линейного преобразования, то другой векторявляетсялинейной комбинациейвекторов.

Определение:Еслитолько при== … == 0, то векторыназываютсялинейно независимыми.

Определение:Если в линейном пространствеLестьnлинейно независимых векторов и любыеn + 1 векторов линейно зависимы, то пространствоLназываетсяn-мерным, а совокупность линейно независимых векторов называетсябазисомлинейного пространстваL.

Следствие:Любой вектор линейного пространства может быть представлен в виде линейной комбинации векторов базиса.

Пусть в n-мерном линейном пространстве с базисом,,…,задано линейное преобразование А. Тогда векторы А,А,…,А- также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

A= a₁₁+ a₂₁+…+ a_n1

A= a₁₂+ a₂₂+…+ a_n2

……………………………….

A=a_n1+a_n2+…+a_nn

Тогда матрица А = называетсяматрицей линейного преобразования А.

Если в пространстве Lвзять вектор =x₁+x₂+…+x_n, тоAL.

, где

……………………………..

Эти равенства можно назвать линейным преобразованием в базисе,,…,.

В матричном виде:

, А,

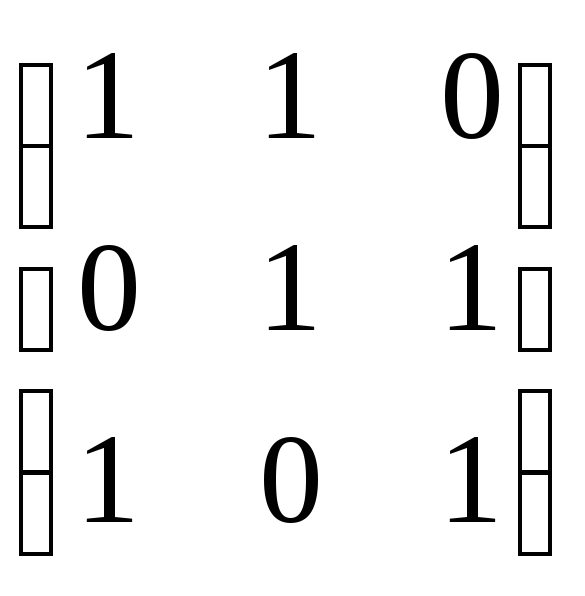
Пример.Найти матрицу линейного преобразования, заданного в виде:

x = x + y

y = y + z

z = z + x

x = 1x + 1y + 0z

y= 0x+ 1y+ 1z

z= 1x+ 0y+ 1z

A=

На практике действия над линейными преобразованиями сводятся к действиям над их матрицами.

Определение:Если векторпереводится в векторлинейным преобразованием с матрицей А, а векторв векторлинейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему векторв вектор(оно называетсяпроизведением составляющих преобразований).

С = ВА

Пример.Задано линейное преобразование А, переводящее векторв вектори линейное преобразование В, переводящее векторв вектор. Найти матрицу линейного преобразования, переводящего векторв вектор.

С = ВА

Т.е.

Примечание:ЕслиА= 0, то преобразование вырожденное, т.е., например, плоскость преобразуется не в целую плоскость, а в прямую.