
- •Высшая математика (краткий курс лекций)
- •§2. Линейные операции над векторами.
- •§3. Линейная комбинация векторов.
- •§4. Скалярное произведение векторов.
- •§5.Векторное произведение векторов.
- •§7. Линейная зависимость векторов
- •§8. Размерность и базис векторного пространства.
- •§9. Евклидово пространство.
- •§9. Линейные операторы.
- •Глава 2. Матрицы и определители.
- •§1. Основные сведения о матрицах.
- •§2. Операции над матрицами.
- •Самым характерным примером может служить единичная матрица, которая является перестановочной с любой квадратной матрицей того же порядка:
- •§3. Определители квадратных матриц.
- •§4.Обратная матрица.
- •Алгоритм вычисления обратной матрицы:
- •§5. Базисный минор матрицы. Ранг матрицы.
- •Глава 3. Системы линейных уравнений.
- •§1. Основные понятия и определения.
- •§2. Система n линейных уравнений с n неизвестными.
- •2.1. Матричный метод (метод обратной матрицы).
- •§3. Метод Гаусса. (Карл Фридрих Гаусс (1777-1855) немецкий математик)
- •§4. Система m линейных уравнений с n переменными.
- •§5. Система линейных однородных уравнений. Фундаментальная система решений.
- •Глава 4. Основы аналитической геометрии.
- •§1.Уравнение линии на плоскости.
- •§2. Уравнение прямой на плоскости. Различные виды уравнений прямой.
- •Уравнение прямой по точке и вектору нормали.
- •Уравнение прямой по точке и угловому коэффициенту.
- •Уравнение прямой, проходящей через две точки.
- •Уравнение прямой по точке и направляющему вектору.
- •Уравнение прямой в отрезках.
- •Нормальное уравнение прямой.
- •Угол между прямыми на плоскости.
- •Расстояние от точки до прямой.
- •§3.Кривые второго порядка. Уравнение вида
- •Окружность.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •§4. Системы координат.
- •Полярная система координат.
- •§5. Аналитическая геометрия в пространстве.
- •5.1.Плоскость в пространстве.
- •Уравнение плоскости, проходящей через три точки.
- •Условия параллельности и перпендикулярности плоскостей.
- •Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой в пространстве, проходящей через две точки.
- •Общие уравнения прямой в пространстве.
- •5. 4.1. Цилиндрические поверхности.
- •5.4.2 Поверхности вращения.
- •Связь цилиндрической и декартовой прямоугольной
- •§7. Собственные значения и собственные векторы линейного преобразования.
- •§7. Квадратичные формы.
- •Приведение квадратичных форм к каноническому виду.
- •Глава 5. Комплексные числа.
- •§1. Определение комплексного числа.
- •§2. Геометрическая интерпретация комплексного числа.
- •§3. Тригонометрическая форма числа.
- •§4. Действия с комплексными числами.
- •§5. Показательная форма комплексного числа.
- •§6. Разложение многочлена на множители.
5. 4.1. Цилиндрические поверхности.
Определение.Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.
Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY(эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:
 -
эллиптический цилиндр.
-
эллиптический цилиндр.

2)
![]() - гиперболический цилиндр.
- гиперболический цилиндр.

x2 = 2py – параболический цилиндр.

5.4.2 Поверхности вращения.
Определение.Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямойd, называетсяповерхностью вращения с осью вращенияd.
Если уравнение поверхности в прямоугольной системе координат имеет вид:
F(x2 +y2,z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.
Аналогично: F(x2 +z2,y) = 0 – поверхность вращения с осью вращения Оу,
F(z2 +y2,x) = 0 – поверхность вращения с осью вращения Ох.
Запишем уравнения поверхностей вращения для некоторых частных случаев:
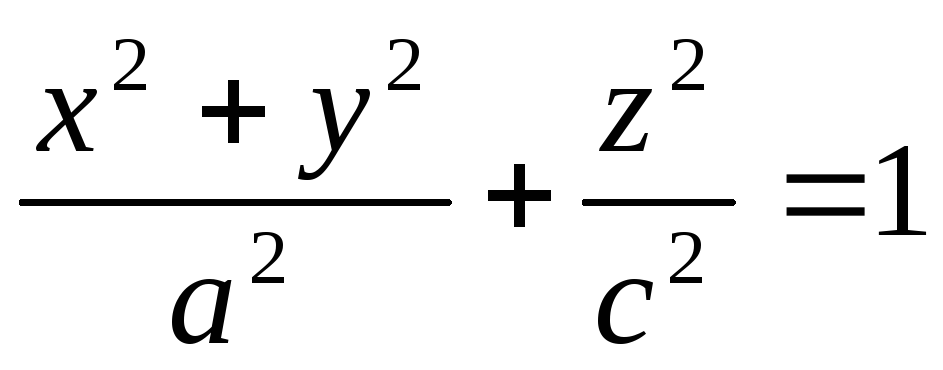 - эллипсоид вращения
- эллипсоид вращения - однополостный
гиперболоид вращения
- однополостный
гиперболоид вращения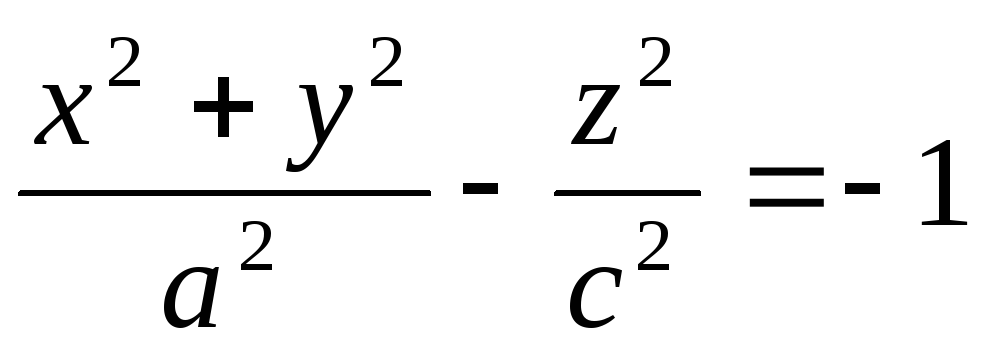 - двуполостный гиперболоид
вращения
- двуполостный гиперболоид
вращения  - параболоид вращения
- параболоид вращения
Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу.
Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:
Сфера:
![]()

Трехосный
эллипсоид:
![]()
В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.

Однополостный
гиперболоид:
![]()

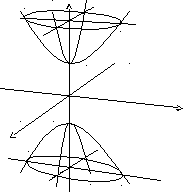
Двуполостный
гиперболоид:
![]()
Эллиптический параболоид:
![]()

Гиперболический
параболоид:
![]()

Конус второго порядка:
![]()

5. 4.3. Цилиндрическая и сферическая системы координат.
Как и на плоскости, в пространстве положение любой точки может быть определено тремя координатами в различных системах координат, отличных от декартовой прямоугольной системы. Цилиндрическая и сферическая системы координат являются обобщением для пространства полярной системы координат, которая была подробно рассмотрена ранее.
Введем в
пространстве точку О и луч l,
выходящий из точки О, а также вектор![]() .
Через точку О можно провести единственную
плоскость, перпендикулярную вектору
нормали
.
Через точку О можно провести единственную
плоскость, перпендикулярную вектору
нормали![]() .
.
Для введения соответствия между цилиндрической, сферической и декартовой прямоугольной системами координат точку О совмещают с началом декартовой прямоугольной системы координат, луч l– с положительным направлением осих, вектор нормали – с осьюz.
Цилиндрическая и сферическая системы координат используются в тех случаях, когда уравнение кривой или поверхности в декартовой прямоугольной системе координат выглядят достаточно сложно, и операции с таким уравнением представляются трудоемкими.
Представление уравнений в цилиндрической и сферической системе позволяет значительно упростить вычисления, что будет показано далее.
 z
z
М
h
0 x
r
M1
y
![]() ОМ1
= r; MM1
= h;
ОМ1
= r; MM1
= h;
Если из точки М опустить перпендикуляр ММ1на плоскость, то точка М1будет иметь на плоскости полярные координаты (r,).
Определение. Цилиндрическими координатами точки М называются числа(r, , h),которые определяют положение точки М в пространстве.
Определение. Сферическими координатами точки М называются числа(r,,),где- угол междуи нормалью.
