
- •Высшая математика (краткий курс лекций)
- •§2. Линейные операции над векторами.
- •§3. Линейная комбинация векторов.
- •§4. Скалярное произведение векторов.
- •§5.Векторное произведение векторов.
- •§7. Линейная зависимость векторов
- •§8. Размерность и базис векторного пространства.
- •§9. Евклидово пространство.
- •§9. Линейные операторы.
- •Глава 2. Матрицы и определители.
- •§1. Основные сведения о матрицах.
- •§2. Операции над матрицами.
- •Самым характерным примером может служить единичная матрица, которая является перестановочной с любой квадратной матрицей того же порядка:
- •§3. Определители квадратных матриц.
- •§4.Обратная матрица.
- •Алгоритм вычисления обратной матрицы:
- •§5. Базисный минор матрицы. Ранг матрицы.
- •Глава 3. Системы линейных уравнений.
- •§1. Основные понятия и определения.
- •§2. Система n линейных уравнений с n неизвестными.
- •2.1. Матричный метод (метод обратной матрицы).
- •§3. Метод Гаусса. (Карл Фридрих Гаусс (1777-1855) немецкий математик)
- •§4. Система m линейных уравнений с n переменными.
- •§5. Система линейных однородных уравнений. Фундаментальная система решений.
- •Глава 4. Основы аналитической геометрии.
- •§1.Уравнение линии на плоскости.
- •§2. Уравнение прямой на плоскости. Различные виды уравнений прямой.
- •Уравнение прямой по точке и вектору нормали.
- •Уравнение прямой по точке и угловому коэффициенту.
- •Уравнение прямой, проходящей через две точки.
- •Уравнение прямой по точке и направляющему вектору.
- •Уравнение прямой в отрезках.
- •Нормальное уравнение прямой.
- •Угол между прямыми на плоскости.
- •Расстояние от точки до прямой.
- •§3.Кривые второго порядка. Уравнение вида
- •Окружность.
- •Эллипс.
- •Гипербола.
- •Парабола.
- •§4. Системы координат.
- •Полярная система координат.
- •§5. Аналитическая геометрия в пространстве.
- •5.1.Плоскость в пространстве.
- •Уравнение плоскости, проходящей через три точки.
- •Условия параллельности и перпендикулярности плоскостей.
- •Уравнение прямой в пространстве по точке и направляющему вектору.
- •Уравнение прямой в пространстве, проходящей через две точки.
- •Общие уравнения прямой в пространстве.
- •5. 4.1. Цилиндрические поверхности.
- •5.4.2 Поверхности вращения.
- •Связь цилиндрической и декартовой прямоугольной
- •§7. Собственные значения и собственные векторы линейного преобразования.
- •§7. Квадратичные формы.
- •Приведение квадратичных форм к каноническому виду.
- •Глава 5. Комплексные числа.
- •§1. Определение комплексного числа.
- •§2. Геометрическая интерпретация комплексного числа.
- •§3. Тригонометрическая форма числа.
- •§4. Действия с комплексными числами.
- •§5. Показательная форма комплексного числа.
- •§6. Разложение многочлена на множители.
§3. Линейная комбинация векторов.
Определение. Линейной комбинацией
векторов![]() ,
,![]() ,
. . .
,
. . .![]() с действительными коэффициентами,, . . .,,
называется вектор
с действительными коэффициентами,, . . .,,
называется вектор![]() .
.
Утверждения:
Если векторы
 и
и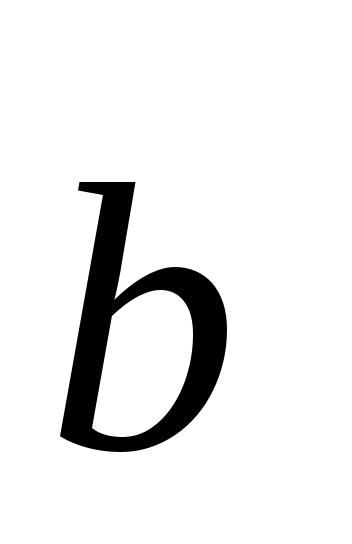 коллинеарны,
то их линейная комбинация с некоторыми
действительными числамии(≠0
и≠0) равна нулю:
коллинеарны,
то их линейная комбинация с некоторыми
действительными числамии(≠0
и≠0) равна нулю: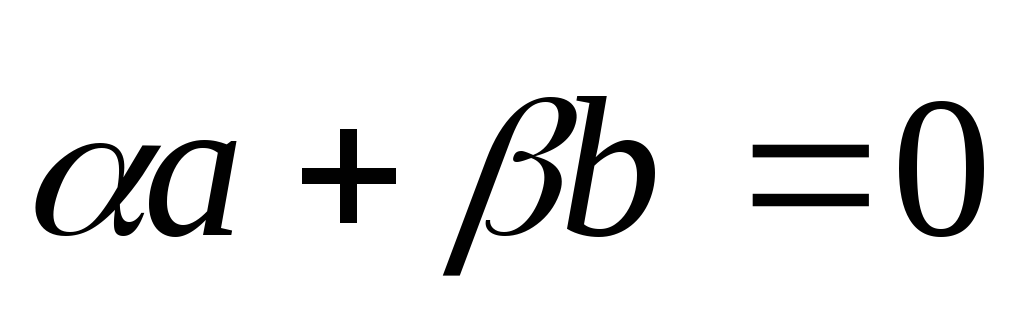
Действительно,
![]() и, наоборот, если
и, наоборот, если![]() ||
||![]()
![]()
(самостоятельно).
Если векторы
 ,
,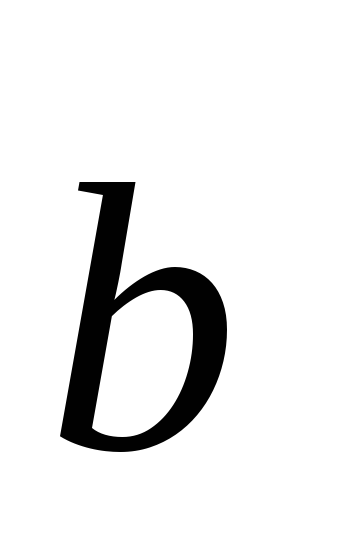 и
и - компланарны, то найдутся такие числа,,(≠0), что их линейная
комбинация будет равна нулю ( и наоборот),
т.е.
- компланарны, то найдутся такие числа,,(≠0), что их линейная
комбинация будет равна нулю ( и наоборот),
т.е.
![]() ,
,![]() и
и![]() - компланарны
- компланарны![]()
Определение.Линейно независимыми векторами на плоскости называются два вектора, если они не коллинеары; а в 3-ех мерном пространстве – три вектора, если они не компланарны.
Определение.Два или три ортогональных (перпендикулярных) вектора являются линейно независимыми и образуют двойку или тройку линейно независимых векторов.
Определение. Если три единичных вектора (длина которого равна единице) взаимно перпендикулярны и образуют правую тройку векторов, то они являются базой прямоугольной декартовой системы координат.
Обозначается
![]() -ортыкоординат.
-ортыкоординат.
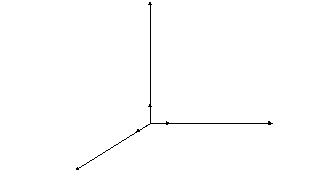 Система
координат называетсяправой,потому
что векторы
Система
координат называетсяправой,потому
что векторы![]() имеют такую же ориентацию, как
соответственно большой, указательный
и средний пальцы правой руки. Для
определения правого направления системы
координат может быть использованоправило правого винта:если винт
вкручивается в осьOZсо
стороны 0, то отвертка вращается отXкY.
имеют такую же ориентацию, как
соответственно большой, указательный
и средний пальцы правой руки. Для
определения правого направления системы
координат может быть использованоправило правого винта:если винт
вкручивается в осьOZсо
стороны 0, то отвертка вращается отXкY.
Вектор
![]() в прямоугольной декартовой системе
координат записывается в виде:
в прямоугольной декартовой системе
координат записывается в виде:![]() ,
гдеax,
ay,
az– прямоугольные декартовы координаты
вектора
,
гдеax,
ay,
az– прямоугольные декартовы координаты
вектора![]() или проекции этого вектора на
соответствующие оси.
или проекции этого вектора на
соответствующие оси.
В прямоугольной декартовой системе
координат каждой точке М однозначно
соответствует вектор
![]() ,
который называется радиус-вектором
точки М. Декартовы координаты вектора
,
который называется радиус-вектором
точки М. Декартовы координаты вектора![]() отнесенные
к
отнесенные
к![]() ,
называются декартовыми координатами
точки М.
,
называются декартовыми координатами
точки М.
§4. Скалярное произведение векторов.
Пусть
![]() и
и![]() - произвольные векторы, а- угол между ними:
- произвольные векторы, а- угол между ними:

![]()
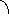

![]()
Определение.
Скалярным произведением векторов![]() и
и![]() называется число, равное произведению
длин этих векторов на косинус угла между
ними:
называется число, равное произведению
длин этих векторов на косинус угла между
ними:

![]()
![]() =
=![]()
![]() cos(3.1)
cos(3.1)
Свойстваскалярного произведения:

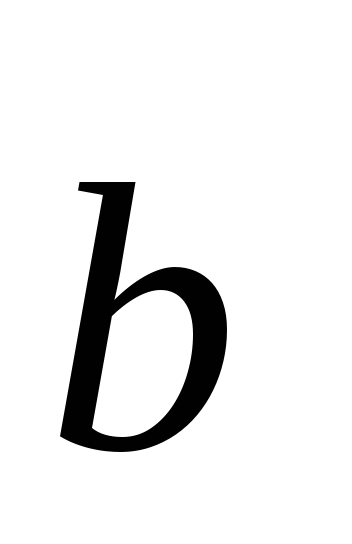 =
=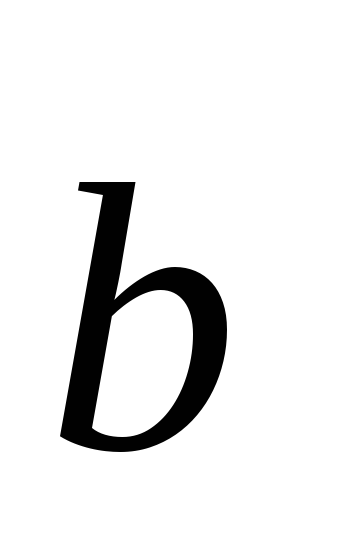
 - переместительный закон;
- переместительный закон;(
 )
) =
= (
(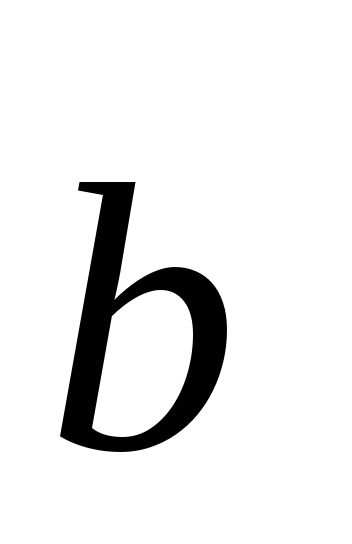 )
=(
)
=(
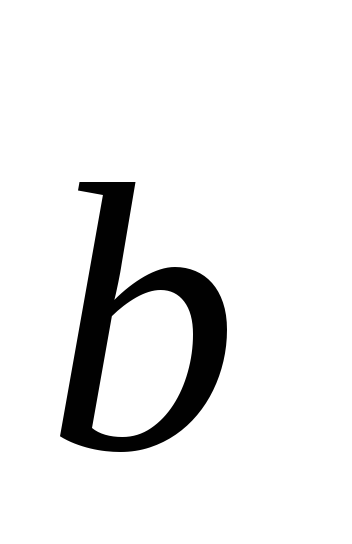 ),=const– сочетательный закон относительно
умножения на число;
),=const– сочетательный закон относительно
умножения на число; (
(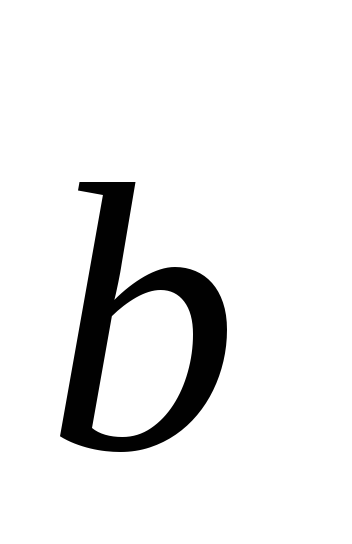 +
+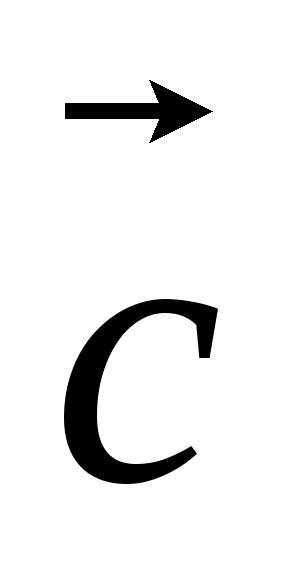 )
=
)
=
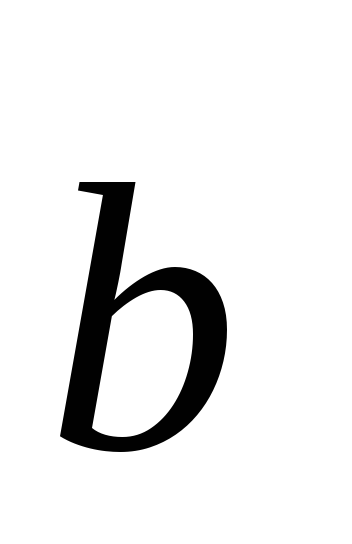 +
+
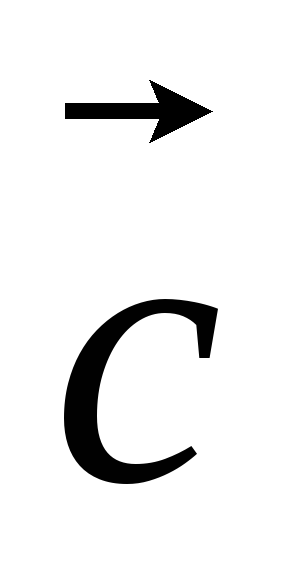 - распределительный закон относительно
суммы векторов;
- распределительный закон относительно
суммы векторов;


 =
= 2=
2= 2(3.2) –формула
скалярного квадрата.
2(3.2) –формула
скалярного квадрата.
![]()
![]() =
=![]()
![]() cos(
cos(![]() ,
,![]() )
=
)
= ![]() 2
cos0
=
2
cos0
= ![]() 2.
2.
Из (3.2) ![]() =
=![]() -длина вектора равна корню квадратному
из его скалярного квадрата.
-длина вектора равна корню квадратному
из его скалярного квадрата.


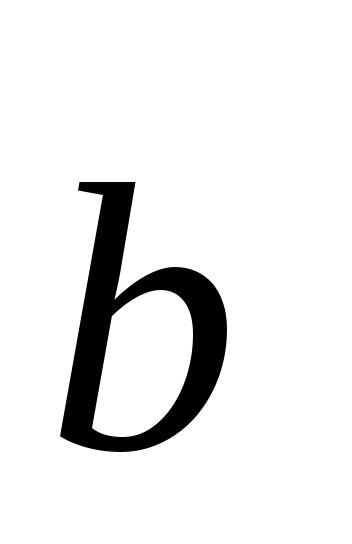 = 0, если
= 0, если
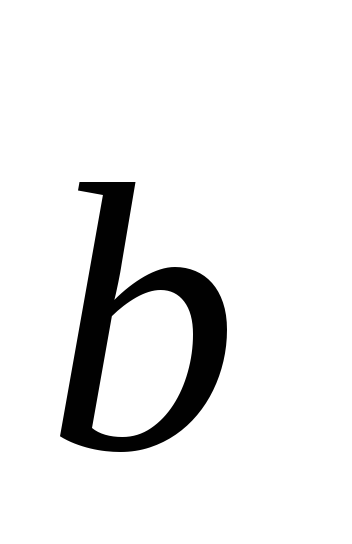 и наоборот, если
и наоборот, если
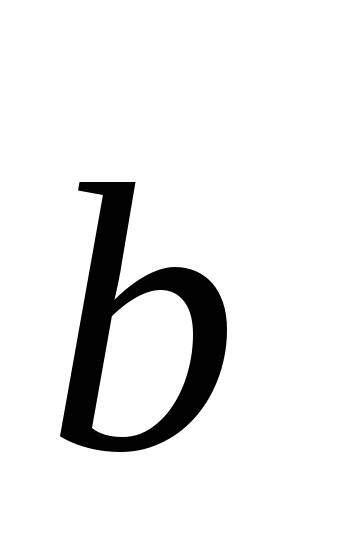 = 0, то при
= 0, то при 0 и
0 и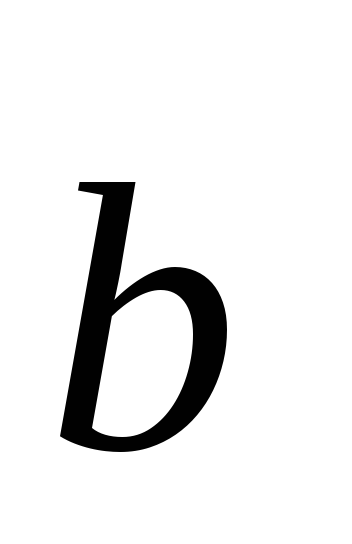 0 векторы
0 векторы и
и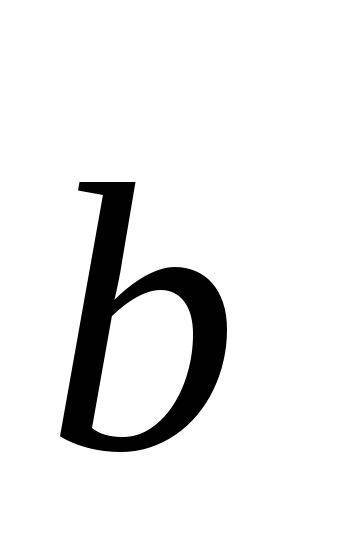 взаимно
перпендикулярны – этоусловие
перпендикулярности двух векторов:
взаимно
перпендикулярны – этоусловие
перпендикулярности двух векторов:
![]()
![]()
![]()
![]() = 0 (3.3)
= 0 (3.3)
Если рассматривать векторы
![]() в
декартовой прямоугольной системе
координат, то
в
декартовой прямоугольной системе
координат, то

![]()
![]() =xa
xb
+ ya
yb
+ za
zb
(3.4) -скалярное произведение
векторов
в координатной форме
=xa
xb
+ ya
yb
+ za
zb
(3.4) -скалярное произведение
векторов
в координатной форме
Используя полученные равенства (3.1) и (3.4), получаем формулу для вычисления угла между векторами:
![]()
 (3.5)
(3.5)
Пример.Найти (5![]() + 3
+ 3![]() )(2
)(2![]() -
-![]() ),
если
),
если![]()
Пример.Найти угол между векторами![]() и
и![]() ,
если
,
если![]()
![]() .
.
Пример.Найти скалярное произведение (3![]() - 2
- 2![]() )(5
)(5![]() - 6
- 6![]() ),
если
),
если![]()
Пример.При какомmвекторы![]() и
и![]() перпендикулярны.
перпендикулярны.
Пример.Найти скалярное произведение векторов![]() и
и![]() ,
если
,
если![]()
