Высшая математика (краткий курс лекций)
I СЕМЕСТР
ЛИНЕЙНАЯ АЛГЕБРА С ЭЛЕМЕНТАМИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.
§1. Вектор. Основные понятия.
Очень часто для построения экономических моделей требуется простая и i = 1, 2, . . .n. компактная форма записи сложных экономических процессов. С этой целью будущим экономистам необходимо знать основные понятия и положения такого раздела математики какматричная алгебра. При изложении материала мы будем опираться на понятия и теоремы школьного курса элементарной математики. Например, определения вещественных (действительных) чисел, декартовой системы координат, отображения, точки, прямой, длины отрезка.
Понятие вектора известно из школьного курса математики, но вспомним основные факты, связанные с ним.
Если про две точки известно, какая из них первая, а какая – вторая, то эту пару точек назовем упорядоченной.
Определение.Отрезок, концы которого упорядочены,
называетсянаправленным отрезком иливектором. Первый из его концов
называетсяначалом,а второй –концомвектора.
В
А
Нулевымвектором называется вектор, начало и
конец которого совпадают. Нулевой вектор
обозначается
.
Длина его равна нулю, а направление –
любое.
Определение.Длиной (модулем)вектора называется расстояние между началом и концом вектора.
Определение.Векторы называютсяколлинеарными, если они расположены на одной или параллельных прямых.
Нулевой вектор коллинеарен любому вектору, так как он не имеет определенного направления.
Определение.Для каждого
ненулевого вектора
вводится понятиепротивоположного
вектора -
,
который коллинеарен данному, имеет
такую же длину, но направлен в
противоположную сторону.
Определение.Векторы называютсякомпланарными, если существует плоскость, которой они параллельны.
Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение.Векторы называютсяравными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.
Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.
Если компланарные векторы привести к одному началу, то они будут лежать в одной плоскости.
В любой системе координат вектор
полностью определяется своими
координатами:
.
Например, пусть в прямоугольной декартовой
системе координатOXYZкоординаты начала и конца вектора
соответственноA(x1,y1,z1)
иB(x2,y2,z2).
Тогда координатами этого вектора будут
являться его проекции на соответствующие
координатные оси и определяются они
формулами:
Очевидно, что длина вектора определяется
по формуле:
.
§2. Линейные операции над векторами.
Определение.Линейными операцияминад векторами называется сложение и умножение на число.
Пусть
даны два вектора
=
(a1, a2,
a3) и
=(b1,
b2, b3).
Суммой
векторов
и
является вектор
,
координаты которого равны суммам
соответствующих координат векторов
и
:с1=а1+b1,
c2=a2+b2,
c3=a3+b3.
Геометрически
можно показать, что для получения суммы
векторов нужно совместить конец вектора
с началом вектора
,
тогда вектор
будет
направлен от начала первого вектора к
концу второго.
+
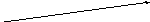
Замечание.Вычитание векторов, как
и в арифметике, есть действие обратное
сложению, т.е. вычесть из вектора
вектор
-
это значит, что к вектору
нужно прибавить вектор, противоположный
вектору
:
-
=
+
(-
)=
=
(а1-b1,
a2-b2,
a3-b3).
Определение.Произведением вектора
0
на число0 называется
вектор
,
координаты которого соответственно
равны(а1,а2,а3).
Геометрический смысл умножения вектора
на число состоит в том, что его длина
изменяется в раз
:
уменьшается, если
< 1 и увеличивается, если
> 1. При этом
коллинеарен
,
причем вектор
сонаправлен с вектором
(
),
если> 0 и вектор
противоположно направлен с вектором
(
),
если< 0.
Основные свойства линейных операций векторов.
Пусть
,
и
-
любые векторы, аи- любые числа.
1)
+
=
+
- коммутативность сложения векторов
(переместительное свойство).
2)
+ (
+
)
= (
+
)+
- ассоциативность сложения векторов
(сочетательное свойство).
3)
+
=
4)
+(-1)
=
5) ()
=(
)
– ассоциативность относительно числовых
множителей (сочетательное свойство
умножения).
6) (+)
=
+
- дистрибутивность относительно суммы
чисел (распределительное свойство).
7) (
+
)
=
+
-
дистрибутивность относительно суммы
векторов (распределительное свойство).
8) 1
=
Пусть даны два вектора
=
(a1, a2,
a3) и
=(b1, b2,
b3).Из
определения коллинеарности векторов
и определения произведения вектора на
число вытекает, что (теорема):векторы
и
коллинеарны
т. и т.т., если их координаты пропорциональны:
(2.1)Условие
коллинеарности двух векторов.
Доказательство:
I) Пусть 
= 
,
т.е. (a1,
a2,
a3)
= (b1,
b2,
b3)
a1=b1
a2=b2 (2.1)
a3=b3
I
I)
Пусть 
=,
тогда a1=b1
a2=b2
= 
,
т.е.
.
a3=b3