Пример решения задачи средствами MathCad

Задача Коши: y’(t) = 2ty, t0 = 0, T = 1,

y(0) = 1.

Исходные данные:

правая часть:

;

начальное значение:

концы отрезка:

шаг сетки:

число узлов сетки:

Функция, реализующая явный метод Эйлера, возвращает вектор решения:

!!!!!

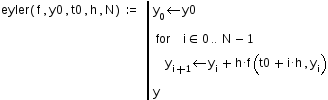
Входные параметры:

f — функция правой части;

y0 — начальное значение;

t0 — начальная точка отрезка;

h — шаг сетки;

N — число узлов сетки.

Вычисление решения по методу Эйлера:

!!!!!

Вычисление решения по методу Рунге-Кутты четвертого порядка точности:

Входные параметры:

y — вектор начальных значений;

t0 — начальная точка отрезка;

T — конечная точка отрезка;

N — число узлов сетки;

f — функция правой части.

Функция rkfixed возвращает матрицу, первый столбец которой содержит узлы сетки, а второй — приближенное решение в этих узлах.

Точное решение:

.

Точное решение в узлах сетки:

.

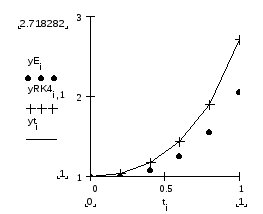
Решение по методу Эйлера, решение по методу Рунге-Кутты, точное решение:

Графики приближенного и точного решений:

Вычисление погрешности по правилу Рунге:

Вычисление приближенных решений с шагом h / 2:

Вычисление погрешностей:

Значение погрешностей:

Варианты индивидуальных заданий

Задача 1. Напишите программу численного решения задачи Коши для обыкновенного дифференциального уравнения первого порядка

на отрезке с шагома) методом Эйлера; б) методом Рунге-Кутты четвертого порядка с оценкой погрешности по правилу Рунге. Найдите точное решение задачи. Постройте на одном чертеже графики точного и приближенных решений. Исходные данные для выполнения задания возьмите из таблицы. Для реализации методов используйте среду программирования и сравните полученные результаты с моделированием средствамиMathCad.

Таблица 4.1 — Индивидуальные задания к задаче 1

№	f(t,y)	t0	T	y0	№	f(t,y)	t0	T	y0
1		1	2	0	16		1	2	1
2			+1	0	17		1	2	3
3		0	1	0	18		1	2	1
4			+1	0,5	19		1	2	1
5		–1	0	1,5	20		1	2
6		0	1	1	21		1	2	1
7			+1	1	22		0	1	3
8			+1		23		0	1	1

Окончание табл. 4.1

9		1	2	1	24		0	1	1
10		0	1		25		0	1	0,5
11		2	3	4	26		0	1	3
12		1	2		27		0	1	–0,5
13		1	2	1	28		1	2	1
14		1	2	4	29		0	1	0
15		1	2	–	30		0	1	–1

Контрольные вопросы

1. На какие основные группы подразделяются приближенные методы решения дифференциальных уравнений?

2. В какой форме можно получить решение дифференциального уравнения по методу Эйлера?

3. Каков геометрический смысл решения дифференциального уравнения методом Эйлера?

4. В какой форме можно получить решение дифференциального уравнения по методу Рунге-Кутта?

5. Какой способ оценки точности используется при приближенном интегрировании дифференциальных уравнений методами Эйлера и Рунге-Кутта?

6. Как вычислить погрешность по заданной формуле, используя метод двойного пересчета?