Контрольные вопросы

1. Постановка задач приближения функций.

2. Метод наименьших квадратов. Вывод нормальной системы метода наименьших квадратов.

3. Обусловленность нормальной системы.

4. Выбор оптимальной степени аппроксимирующего многочлена.

5. Полиномиальная интерполяция. Многочлен в форме Лагранжа.

6. Многочлен в форме Ньютона.

7. Погрешность интерполяции.

8. Интерполяция с кратными узлами.

9. Минимизация оценки погрешности интерполяции.

Лабораторная работа 3 численное интегрирование и дифференцирование функций

Цель: изучить и научиться программировать методы приближенного вычисления определенных интегралов, основанные на квадратурных формулах Ньютона-Котеса.

Постановка задачи численного интегрирования и методы её решения

Чаще всего для приближенного вычисления определенного интеграла используются квадратурные формулы Ньютона-Котеса. Погрешность таких формул оценивается порядком их алгебраической точности — порядком полинома, при подстановке которого в качестве подынтегральной функции формула дает точный результат.

Простой прием построения квадратурных формул состоит в том, что подынтегральная функция заменяется на отрезкеинтерполяционным многочленом, например, многочленом Лагранжа; для интеграла имеем приближенное равенство (3.1). Предполагается, что отрезок разбит начастей точками (узлами), наличие которых подразумевается при построении многочлена. Для равноотстоящих узлов

. (3.1)

При определенных допущениях получаем формулу трапеций:

(3.2)

где — значения функции в узлах интерполяции.

Имеем следующую оценку погрешности метода интегрирования по формуле трапеций (3.2):

где ,(3.3)

Во многих случаях более точной оказывается формула Симпсона (формула парабол)

(3.4)

Для нее имеем следующую оценку погрешности:

где ,.

Блок-схема метода Симпсона приводится на рисунке 3.1:

Рисунок. 3.1 — Блок-схема алгоритма метода Симпсона

Пример. Вычислить значение интеграла , где , с помощью квадратурных формул трапеций и Симпсона для элементарного отрезка интегрирования. Оценить величину погрешности. Применяя те же квадратурные формулы для составного отрезка интегрирования, вычислить интеграл с точностью 0.0001. Предварительно оценить шаг интегрирования, при котором достигается заданная точность.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Вычисляем значение интеграла аналитически.

2. Задан многочлен . Вычисляем значение интеграла по формулам трапеций и Симпсона, считая отрезокэлементарным отрезком интегрирования.

3. Находим абсолютные погрешности результатов.

4. Используя выражение для остаточных членов интегрирования, оцениваем шаги интегрирования, при которых величина погрешности каждой квадратурной формулы будет меньше 0,0001.

5. Вычисляем значения интеграла по составной квадратурной формуле с найденным шагом.

6. Находим абсолютные погрешности результатов.

Решение задачи средствами MathCad

Многочлен ;

коэффициенты многочлена: ,,,;

концы отрезка интегрирования: ;

значение интеграла, вычисленное аналитически: ;

элементарная формула левых прямоугольников: ;

абсолютная погрешность: .

Определение максимума модуля производной M1 многочлена на отрезке [a, b]:

• теоретическая оценка погрешности ;

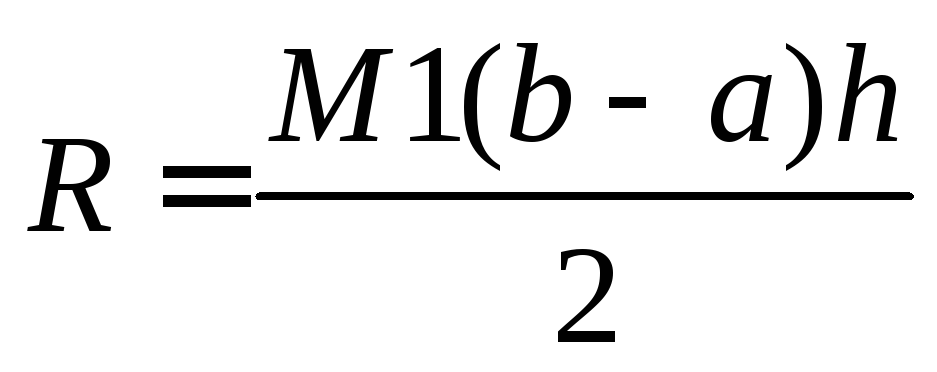
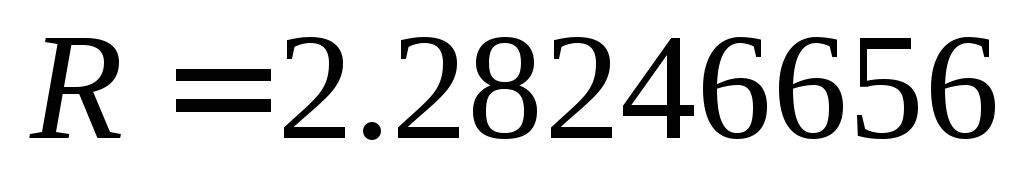• составная формула левых прямоугольников .

Вычисление по составной формуле левых прямоугольников с найденным шагом h: