Iзотермiчний процес

Характеристика процесу: Т = соnst , dТ = О.

Робота газу. Щоб визначити роботу газу iнтегруванням виразу елементарної роботи, зведемо спочатку цей вираз до однiєї змiнної. Визначивши з рiвняння Клапейрона—Менделєєва Р i пiдставивши його значення у формулу для об-числення роботи, дiстанемо

,

проiнтегрувавши останнiй вираз, знайдемо

(2.27)

Замiсть вiдношення об’ємiв у вираз (2.27) можна пiдставити за законом Бойля—Марiотта обернене до нього вiдношення тискiв.

(2.28)

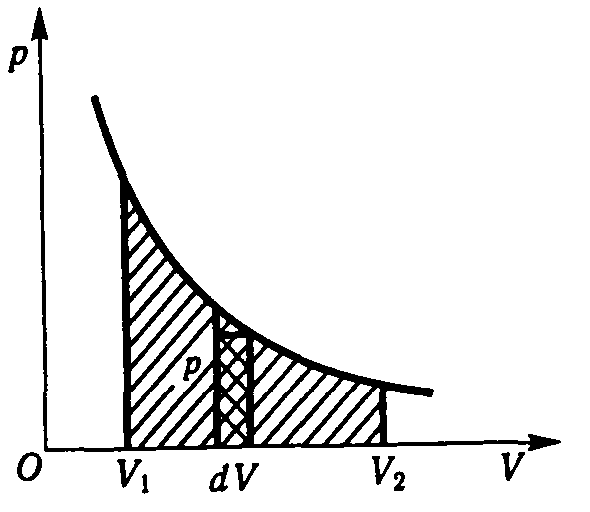
Рис.2.10

Графiчно на дiаграмi р,V (рис. 2.10) робота газу в iзотермiчному процесi дорiвнює площi фiгури, обмеженої графiком стану газу (iзотермою), вiссю об’ємiв та ординатами, що вiдповiдають початковому i кiнцевому тискам газу.

Кiлькiсть теплоти. Для iзотермiчного процесу dТ = 0; тому dU = 0, тобто внутрiшня енергiя iдеального газу в цьому процесi залишається сталою. Застосувавши до цього процесу перший закон термодинамiки, дiстанемо

, Q =А. (2.29)

Отже, в iзотермiчному процесi вся теплота, яку дiстає газ, витрачається на виконання роботи.

Молярна теплоємність при ізотермічному процесі

(2.30)

Отже , поняття теплоємності при ізотермічному процесі не має сенсу.

Iзохоричний процес

Характеристика процесу: V =соnst , dV = 0.

Робота газу. Оскiльки для iзохоричного процесу dV = 0, елементарна робота газу дорiвнюс нулю:

=0

i робота газу для всього процесу дорiвнює нулю:

А =0. (2.31)

Кiлькiсть теплоти. Застосувавши вираз першого закону термодинамiки до iзохоричного процесу та врахувавши, що в цьому процесi , отримаємо

(2.32)

Проiнтегрувавши цей вираз, знайдемо

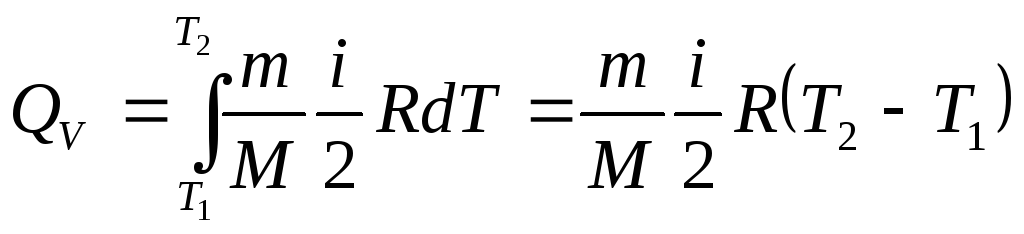(2.33)

В ізохоричному процесі вся теплота, яку дістає газ, витрачається на збільшення його внутрішньої енергії; при цьому температура газу підвищується.

Молярна теплоємність при ізохоричному процесі

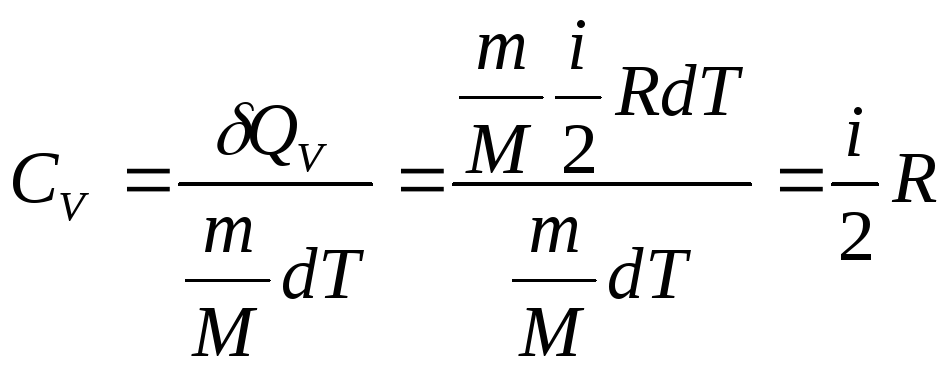(2.34)

Адіабатний процес

Адіабатний процес– це процес, який протікає без теплообміну газу із зовнішнім середовищем (тобто ). Якщо покласти у рівнянні першого закону термодинаміки

, (2.35)

то отримаємо рівняння адіабати ідеального газу:

pV ^=const, (2.36)

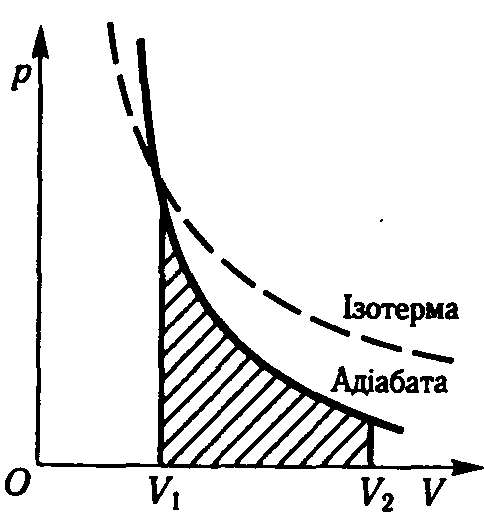
Рис.2.11

де  = C_p / C_V = (i+2)/i,  – коефіцієнт адіабати, який визначається кількістю ступенів вільності i молекули. Формула (2.36) має назву рівняння Пуассона.

Графiчно на дiаграмi рV адiабатний процес зображується кривою, яка називається адiабатою (рис. 2.11). Тому рiвняння (2.36) iнакше називають рiвнянням адiабати. Порiвняно з iзотермою адiабата є гiперболою вищого порядку, вона крутiша вiд iзотерми.

Наведемо формули для обчислення роботи газу в адiабатному процесi.

За першим законом термодинамiки для адiабатичного процесу iдеального газу маємо

. (2.37)

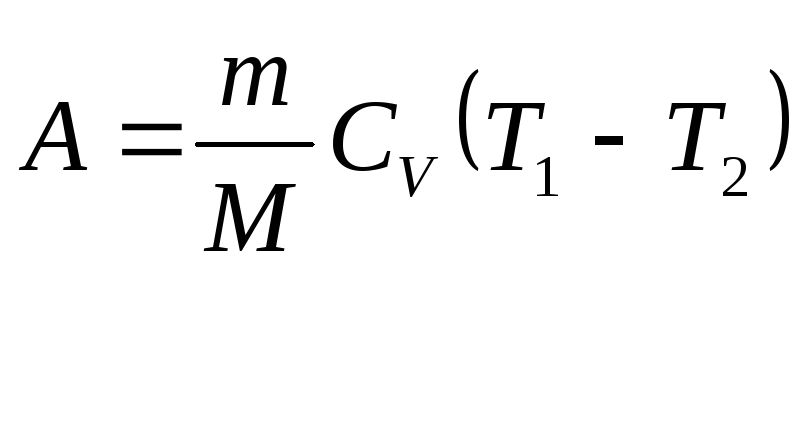. (2.38)

Якщо за рівнянням Клапейрона-Менделєєва визначити температуру і підставити її у вираз (2.38),то дістанемо

. (2.39)

Графiчно робота газу в адiабатному процесi визначається площею так само, як i в iнших процесах ( рис. 2.11).