Кінетична теорія газів

У молекулярно – кінетичній теорії користуються моделлю ідеального газу, що задовільняє таким умовам :

1) власний об’єм молекул нехтовно малий порівняно з об’ємом посудини;

2) між молекулами газу відсутні сили взаємодії;

3) зіткнення молекул газу між собою і з стінками посудини абсолютно пружні.

Рівняння стану ідеального газу

Рівняння стану ідеального газу називають рівнянням Клапейрона-Менделєєва. У розрахунку на 1 моль ідеального газу рівняння Клапейрона –Менделєєва записують так:

PV=RT, ( 2.1)

а для будь-якої маси m–так:

PV=RT, (2.2)

де М-маса , яку має моль газу,

Р - тиск газу,

V - об’єм газу,

Т - температура газу,

R-універсальна газова стала, R=8, 31.

Основне рівняння молекулярно-кінетичної теорії ідеального газу

Тиск газу на стінки посудини обумовлений співударами молекул зі стінками і передачею їм імпульсу. При цьому виникає тиск газу на стінки, який дорівнює

, (2.3)

де n – кількість молекул в одиниці об’єму, m₀ –маса однієї молекули,<_кв> - середня квадратична швидкість,

. (2.4)

Рівняння (2.3) називають основним рівнянням МКТ ідеального газу. Перепишемо рівняння (2.3) у вигляді:

,

де - середня кінетична енергія поступального руху однієї молекули газу,

=.

Оскільки ,то =,

де Т-абсолютна температура, к-стала Больцмана, к=1,38*10^-23Дж/моль*К.

Отже, середня кінетична енергія поступального руху молекул ідеального газу залежить тільки від його абсолютної температури. Абсолютна температура є міра середньої кінетичної енергії поступального руху молекул.

Розподіл молекул за швидкостями

Молекули газу рухаються з різними швидкостями. При цьому величини і напрямки швидкостей кожної молекули безперервно змінюються через зіткнення. Можливі значення швидкості молекул лежать у межах від 0 до ∞. Дуже великі і дуже малі порівняно з середніми швидкості мало ймовірні.

Розподіл молекул газу за швидкостями визначається функцією розподілу Максвелла, яка має вигляд:

. (2.5)

(тут m – маса молекули, – її швидкість,А – стала, яка залежить від m та T ).

(2.6)

Функція розподілу f () визначає густину ймовірності, тобто ймовірність того, що швидкість молекул лежить у заданому одиничному інтервалі швидкостей. Тодіf ()dвизначає ймовірність того, що швидкість молекул лежить в інтервалі швидкостей віддо +d. Одночасноf ()dвизначає відносну кількість молекул, швидкості яких лежать в інтервалі швидкості віддо +d, чисельно дорівнює площі заштрихованої ді-

лянки dS на рис.2.1.

Рис.2.1

Вся площа, обмежена кривою розподілу і віссю абсцис , чисельно дорівнює числу молекул, швидкості яких мають різні значення від 0 до ∞ . Оскільки цій умові задовільняють всі n молекул , то площа дорівнює одиниці:

(2.7)

Швидкість, що відповідає максимуму функції розподілу f (), називається найбільш ймовірною швидкістю (див. рис. 2.1)

, де m₀ – маса молекули, k – стала Больцмана, T – абсолютна температура. Знаючи розподіл молекул за швидкостями, можна визначити середнє значення швидкості молекул газу:

. (2.8)

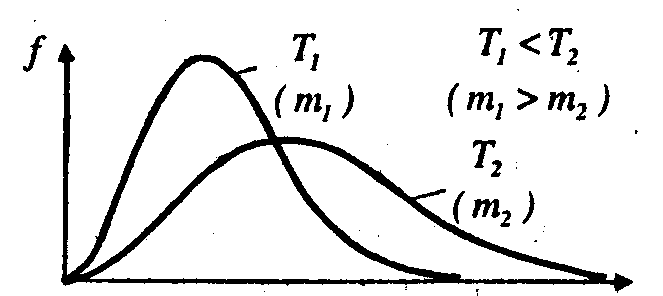
При збільшенні температури (або зменшенні маси молекул ) максимум кривої f () зміщується у бік більших швидкостей , а його абсолютна величина зменшується, причому площа ,яка охоплена кривоюf () і віссю, залишається незмінною(рис.2.2).

Рис.2.2

Функція (2.5) розподілу молекул газу за швидкостями одночасно є і функцією розподілу молекул газу за кінетичними енергіями:

, (2.9)

де _k– кінетична енергія молекул, А – стала, що залежить від m та T .