Научное помсобие 1All Tom 1 UA

Електростатика. Постійний струм

§44 Електрорушійна сила. Напруга

Для виникнення і підтримки в провідниках струму провідності на заряджені частинки повинні діяти сили, що забезпечують їх впорядковане переміщення протягом кінцевого проміжку часу.

Усередині провідника, у якому протікає постійний електричний струм, на заряд діють такі сили.

1.Електростатичні (кулонівські) сили, під дією яких позитивні заряди рухаються уздовж поля, негативні – проти. Поле цих сил називають кулонівським, напруженість поля позначають Eкул .

2.Сили не електростатичного походження. Їх називають сторонніми, а поле цих сил – полем сторонніх сил. Напруженість цього поля позначають Eстор .

Необхідність сторонніх сил пояснюється таким чином. Електростатичне поле, створюване в металевому провіднику електронами і позитивно зарядженими іонами кристалічних ґрат, приводить до такого розподілу зарядів, при якому напруженість електричного поля усередині провідника є рівною нулю, а потенціали всіх точок провідника однакові (див. §41). Тому електростатичне поле не може бути причиною постійного електричного струму в провіднику.

Щоб підтримувати струм тривалий час, потрібно збудити і підтримувати усередині провідника електричне поле. Для цього в колі повинен працювати пристрій, в якому відбувається розділення зарядів. Цей пристрій називають

джерелом струму.

Розділення зарядів усередині джерела можливе лише за допомогою сил не електростатичного походження, які називають сторонніми. При цьому сторонні сили повинні виконувати роботу. Ця робота виконується за рахунок деякого запасу механічної, теплової або хімічної енергії.

Робота з переміщення заряду уздовж провідника в процесі протікання по ньому електричного струму виконується і кулонівськими, і сторонніми силами. Повна робота з переміщення заряду

Величина, що чисельно дорівнює відношенню повної роботи, що виконана електростатичними і сторонніми силами з переміщення заряду, до величини цього заряду називається напругою або спадом напруги на даній ділянці кола.

[U ] = ДжКл = В (вольт) .

149

Електростатика. Постійний струм

Величина, що чисельно дорівнює відношенню роботи, що виконана сторонніми силами з переміщення заряду, до величини цього заряду називається

Підставивши записані вирази в (44.2), отримаємо:

Ділянку, на якій на носії заряду діють сторонні сили, називають неоднорідною. Ділянку кола, на якій не діють сторонні сили, називають однорідною.

Для однорідної ділянки (ε = 0):

тобто напруга на однорідній ділянці співпадає з різницею потенціалів на кінцях ділянки.

§45 Закон Ома

45.1 Закон Ома для однорідної ділянки кола. Опір

Німецький фізик Г. Ом* експериментально встановив закон, згідно з яким

сила струму, який тече по однорідному металевому провіднику, пропорційна напрузі на цьому провіднику:

де R – електричний опір. [R] = Ом.

Електричний опір (R) – скалярна фізична величина, що характеризує властивість провідника протидіяти пропусканню електричного струму і дорівнює відношенню напруги U на кінцях провідника до сили струму I, що протікає по ньому:

Опір провідників, наявність електричного струму в яких приводить до виділення тепла, називається омічним або активним. Опір провідника залежить

________________________________________________________________________________

*Ом Георг Симон (1787–1854), німецький фізик.

150

Електростатика. Постійний струм

від матеріалу провідника і його геометричних розмірів. Для однорідного циліндричного провідника воно може бути розраховано за формулою:

де l – довжина провідника;

S – площа поперечного перерізу провідника; ρ – питомий електричний опір.

Питомий електричний опір провідника – величина, що характеризує ма-

теріал провідника і чисельно дорівнює опору однорідного циліндричного провідника одиничної довжини і одиничної площі поперечного перерізу.

[ρ] = Ом м.

Опір металів залежить від температури. З великим ступенем точності можна вважати, що залежність опору металів від температури є лінійною:

де R – опір за температурою t,°С

R0 – опір за 0°С

α – температурний коефіцієнт опору.

Температурний коефіцієнт характеризує температурну стабільність матеріалу і чисельно дорівнює відносній зміні опору провідника при зміні температури на 1 K.

Для чистих металів температурний коефіцієнт опору є величиною порядку α ≈ 0,004 K−1. Для деяких електротехнічних сплавів (манганин, константан) α настільки малий, що їм можна нехтувати і в достатньо широкому інтервалі температур вважати опір незалежним від температури.

Величина G, яка є зворотною опору, називається електропровідністю:

При розгляді фізичної природи питомого електричного опору використо-

вують поняття питомої електричної провідності (електропровідності) σ.

Питома електропровідність σ пов’язана з питомим електричним опором ρ співвідношенням:

[σ] = Ом1 м = Смм .

________________________________________________________________________________

*Сименс Ернст Вернер (1816–1892), німецький електротехнік і промисловець, іноземний член-кореспондент Петербурзької академії наук з 1882 р.

151

Електростатика. Постійний струм

Залежність сили струму від напруги називається вольт-амперною характеристикою (ВАХ). Для металів ця залежність має лінійний характер (рис. 45.1). Для неомічних пристроїв ВАХ має нелінійний характер.

У разі паралельного з’єднання провідників сила струму в нерозгалуженій частині кола дорівнює сумі сил струмів, що течуть в розгалужених ділянках кола, напруга на паралельно з’єднаних ділянках кола однакова.

Раніше було доведено (див. формулу (44.6)), що напруга між двома точками електричного кола вимірюється роботою, що виконується електростатичними і сторонніми силами під час переміщення по колу одиничного позитивного заряду з першої точки в другу, тобто дорівнює сумі різниці потенціалів і електрорушійної сили:

U = ϕ1 − ϕ2 + ε .

152

Електростатика. Постійний струм

задачах електростатики і задачах на струм, де розглядаються ділянки кола, що не містять ерс, поняття напруги і різниці потенціалів часто ототожнюють.

де r – опір джерела струму; R – опір навантаження; (R+r) – повний опір кола.

З наведеного вище визначення напруги виходить, що за наявності сторонніх сил його необхідно застосовувати завжди до конкретної ділянки кола, що поєднує дані точки.

Щоб безпомилково застосовувати закон Ома (45.10) для ділянки кола, що містить ерс, необхідно дотримуватися наступних принципів:

а) накреслити схему і позначити на ній полюси всіх джерел, а також напрям струму в колі (якщо він невідомий, то треба вказати передбачуваний напрям);

б) струм вважати позитивним на заданій ділянці 1-2, якщо він направлений від точки 1 до точки 2;

в) ерс вважати позитивною на ділянці 1-2, якщо вона підвищує потенціал в напрямі від точки 1 до точки 2, тобто при уявному русі уздовж шляху 1-2 спочатку зустрічається негативний полюс джерела, а потім позитивний.

45.3 Закон Ома в диференціальній формі

Перетворимемо закон Ома для ділянки кола (див. формулу (45.1)). Замінимо силу струму через густину струму:

I = j S ;

напругу на кінцях провідника – через напруженість поля:

U = El ;

опір – через геометричні розміри провідника:

R = ρ Sl .

Зробимо підстановку у формулу (45.1):

153

Електростатика. Постійний струм

Густина струму пропорційна напруженості поля в даній точці прові-

дника. Цей вираз називається законом Ома в диференціальній формі.

§46 Розгалужені кола. Правила Кірхгофа

Розрахунок розгалужених електричних кіл постійного струму значно спрощується, якщо використовувати правила, які сформульовані Кірхгофом*.

i=1

Струми вважаються позитивними, якщо вони підходять до вузла. Струми, що відходять від вузла, вважаються негативними.

Для вузла А, зображеного на рис. 46.1, перше правило запишеться таким чином:

I1 + I2 + I3 − I4 − I5 = 0 .

Друге правило: у будь-якому замкненому контурі, довільно обраному в розгалуженому електричному колі, алгебрична сума добутків сил струмів Ii на опори Ri відповідних ділянок цього контуру дорівнює алгебричної сумі ерс, які діють у даному контурі:

де Ii – сила струму на i-й ділянці; Ri – активний опір i-ї ділянки; εi – ерс джерел

струму на i-й ділянці; N – число ділянок, що містять активний опір; k – число джерел струму.

________________________________________________________________________________

*Кірхгоф Густав Роберт (1824–1887), німецький фізик.

154

Електростатика. Постійний струм

Розрахунок розгалуженого кола постійного струму проводиться в такій послідовності:

1)довільно обираються напрями струмів у всіх ділянках кола і напрям обходу контуру;

2)записуються (n–1) незалежних рівнянь правила вузлів, де n – число вузлів в колі;

3)довільні замкнені контури виділяються так, щоб кожний новий контур містив, принаймні, одну ділянку кола, що не входить в раніше розглянуті контури;

4)якщо струми співпадають з обраним напрямом обходу контуру, то вони вважаються додатними. ЕРС вважаються додатними, якщо вони підвищують потенціал у напрямі обходу

контуру.

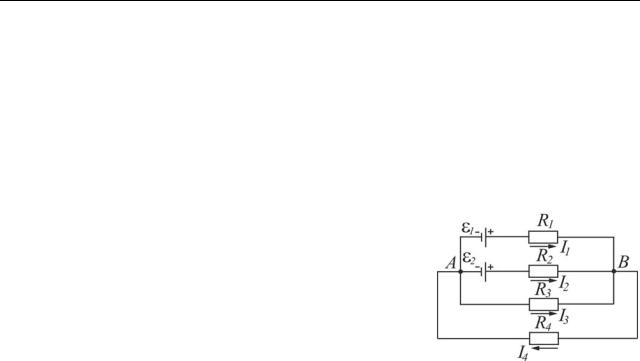
Для контуру AR1BR2A (рис. 46.2) друге правило Кірхгофа запишеться таким чином:

§47 Робота і потужність струму. Закон Джоуля − Ленца

При впорядкованому русі заряджених частинок в провіднику електричне поле виконує роботу. Її прийнято називати роботою струму.

Розглянемо довільну ділянку кола постійного струму, до кінців якого прикладена напруга U. За час t через переріз провідника проходить заряд q = It .

Це дорівнюється тому, що заряд It переноситься за час t з одного кінця провід-

ника в іншій. При цьому сили електростатичного поля і сторонні сили, які діють на даній ділянці, виконують роботу:

Нагадаємо, що згідно з (44.1) напруга U визначається як робота, що виконана електростатичними і сторонніми силами під час переміщення одиничного позитивного заряду.

Поділивши роботу А на час t, за який вона виконується, отримаємо потужність, що розвивається струмом на даній ділянці кола:

Ця потужність може витрачатися на виконання роботи даною ділянкою кола над зовнішніми тілами, на протікання хімічних реакцій, на нагрівання даної ділянки кола і т.п.

Якщо провідник нерухомий і в ньому не відбувається хімічних перетворень, то робота поля по переміщенню зарядів йде на зміну внутрішньої енергії

155

Електростатика. Постійний струм

провідника, тобто провідник нагрівається. При цьому виділяється кількість тепла:

Q = A = IU t .

Від формули (47.3), що визначає тепло, яке виділяється у всьому провіднику, можна перейти до виразу, що характеризує виділення тепла у різних місцях провідника. Оскільки

де lS =V – об’єм провідника.

Розділивши (47.4) на об’єм V на час dt, знайдемо кількість тепла Qпит, що виділяється в одиниці об’єму за одиницю часу (питому теплову потужність):

Формула (47.6) є диференціальною формою закону Джоуля − Ленца.

§48 Електричні вимірювання

48.1 Прилади електровимірювань

Прилад електровимірювання – це сукупність технічних засобів, за допомогою яких відбувається вимірювання тієї або іншої електричної величини. Прилади електровимірювання поділяються на прилади безпосередньої оцінки і прилади порівняння. У приладах безпосередньої оцінки величина, що вимірюється, визначається безпосередньо за положенням стрілки на шкалі приладу або світлового «зайчика» на градуйованій шкалі. В цифрових приладах інформацію знімаються із цифрового табло. До таких приладів відносяться амперметри, вольтметри, ватметри, омметри, гальванометри. До приладів порівняння відносяться численні компенсатори й електричні мости. У них величина, що вимірюється, визначається порівнянням з відомою однорідною величиною.

____________________________________________________________________

*Джоуль Джеймс Преськотт (1818–1889), англійський фізик. *Ленц Еміль Християн (1804–1865), російський фізик.

156

Електростатика. Постійний струм

Для вимірювання електричних величин у приладах безпосередньої оцінки використовуються фізичні явища, що створюють обертальний момент і переміщення рухомої системи приладу. Обертальний момент може бути створений взаємодією магнітного поля постійного магніту і струму в котушці, магнітного поля котушки із струмом і феромагнетика, взаємодією магнітних полів котушок із струмом, взаємодією заряджених тіл. Залежно від того, які явища взаємодії використовуються в приладах, розрізняють такі системи приладів електровимірювання: магнітоелектричну, електромагнітну, електродинамічну, індукційну, електростатичну, термоелектричну і т.п.

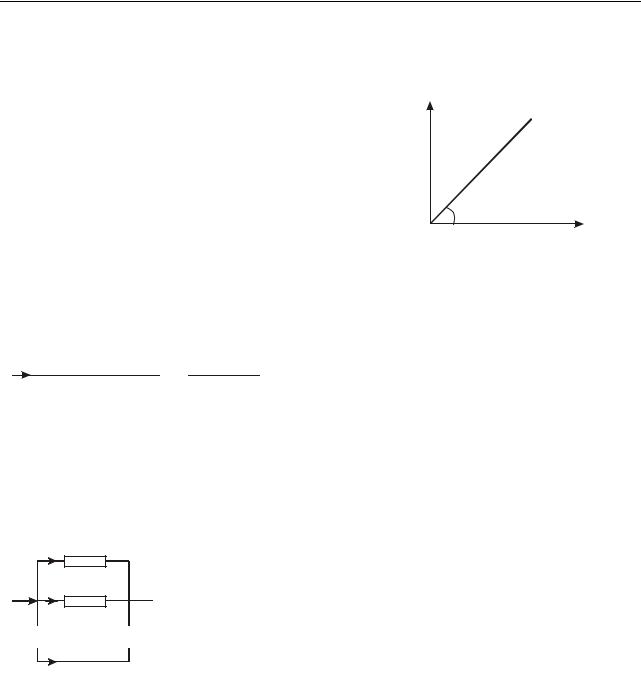
1. Силу струму в колі вимірюють амперметрами, міліамперметрами, мікроамперметрами. Ці прилади включають в коло послідовно. На рис. 48.1 показано їх умовне зображення на схемах.

намагатися виміряти силу струму в освітлювальній мережі, підключаючи амперметр до розетки. Відбудеться коротке замикання: сила струму при малому

який розрахований амперметр; I – струм в колі.

Струм Iш, що проходить через шунт, за законами паралельного з’єднання дорівнює:

Напруга на амперметрі UA дорівнює напрузі на шунті Uш: UА=Uш. За законом Ома для однорідної ділянки кола:

де RA – опір амперметра;

Rш – опір шунта.

I0 RA = IшRш .

157

Електростатика. Постійний струм

Звідси:

Rш = I0IRА .

ш

Замінивши I ш за формулою (48.1), отримаємо

Таким чином, опір шунта має бути в (n–1) разів менше від опору амперметра.

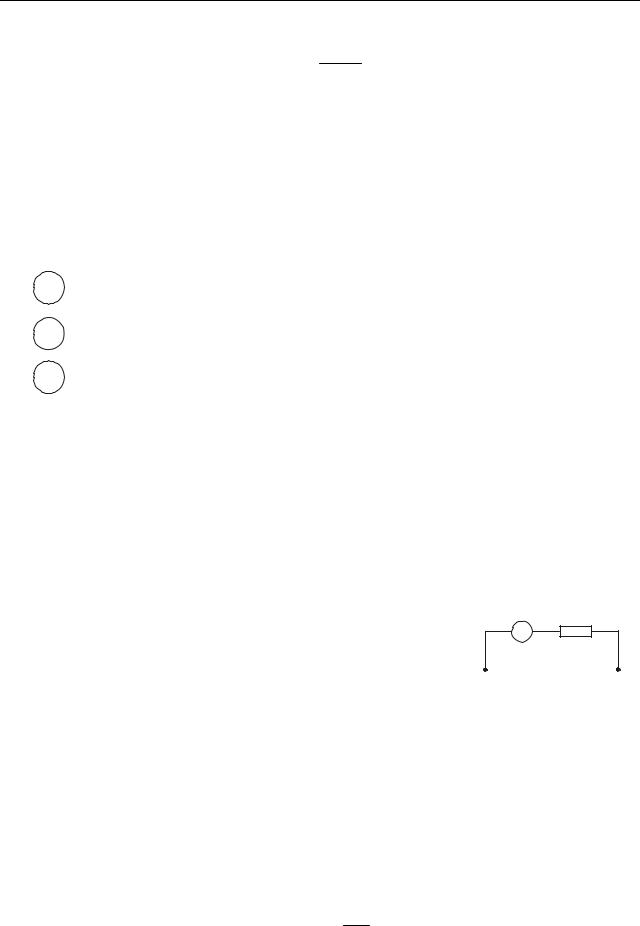
2. Напругу вимірюють вольтметрами, мілівольтметрами і т.п. Ці прилади включають в коло паралельно ділянці, на якій вимірюється напруга. На рис. 48.3 показано їх умовне зображення на схемах.

ся. Для того, щоб вольтметр не вносив помітних спотворень в напругу, що вимірюється, його опір має бути більшим порівняно з опором ділянки кола, на якій вимірюється напруга. Вольтметр можна включати в мережу без ризику, що він згорить, якщо тільки він розрахований на напругу, що перевищує напругу в мережі.

Щоб розширити межі вимірювання напруги в n раз V RД і виміряти напруги до значень U >U0 , послідовно

Потрібно розширити межі вимірювання, тобто зробити можливим вимірювання напруг в n разів більших, ніж вказано на шкалі приладу:

U = nU0

Без зовнішнього додаткового опору межа вимірювань вольтметра дорівнює U0 . Струм, що відхиляє стрілку вольтметра на всю шкалу, визначається за зако-

ном Ома:

I = U0 .

RV

158