Научное помсобие 1All Tom 1 UA

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донецкий национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2. ρ = ρ0 (1 + αt)

3. ρ = ρ0 e 2kT

4. ρ = ρ0αt

.pdf

Скачиваний:

118

Добавлен:

03.03.2016

Размер:

3.85 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2318 19 20 21 22 23 > Следующая >>>

Електростатика. Постійний струм

41.Три провідники, опори яких R1, R2, R3, сполучені паралельно. Які з перерахованих нижче тверджень справедливі?

I0 = I1 + I2 + I3

U0 =U1 =U2 =U3

U0 =U1 +U2 +U3

R0 = R1 + R2 + R3

I0 = I1 = I2 = I3

I0 = I1 + I2 + I3

U0 =U1 +U2 +U3

U0 =U1 =U2 =U3

R0 = R1 + R2 + R3

42.

Вкажіть формулу залежності опору провідника від температури.

1. R =

2. R = R (1 + αt)

3. R = R e αt

4. R = R αt

43.

Вкажіть формулу, за якою розраховується опір провідника.

1. R = ρ

2. R = R (1 + αt)

3. R =

4. R =UI

44.Вкажіть формулу залежності питомого електричного опору провідника від температури.

45.Питомим опором провідника називається …

1)відношення напруги на ділянці кола до сили струму.

2)величина, зворотна опору ділянки кола.

3)добуток сили струму на опір.

4)опірпровідниказавдовжки 1 м, площеюпоперечногоперерізу1 м2.

5)величина, зворотнапитомійпровідностіділянкикола.

46.Питомоюпровідністюділянки коланазивається…

1)відношення напруги на ділянці кола до сили струму.

2)величина, зворотна опору ділянки кола.

3)добуток сили струму на опір.

4)опірпровідниказавдовжки 1 м, площеюпоперечногоперетину1 м2.

5)величина, зворотнапитомомуопору.

47.Вкажіть буквене позначення і одиницю вимірювання кожної з перерахованихвеличин. Приклад: Сила – F – Н (ньютон).

Заряд, потенціал, лінійна густина заряду, поверхнева густина заряду, напруженість електричного поля, електроємність.

48.Вкажіть буквене позначення і одиницю вимірювання кожної з перерахованихвеличин. Приклад: Сила – F – Н (ньютон).

Сила струму, густина струму, напруга, опір, питомий опір, електрорушійна сила, провідність, питома провідність.

169

Електростатика. Постійний струм

49.Вкажіть формули, за якими розраховується потужність електричного струму.

1.	P = IU	2.	P =	U 2	3. P = j2ρ		4. P = I 2 R
				R

50. Вкажіть формули, що виражають закон Джоуля –Ленца.
				t		ε	4. Q = U + A
1.	Q = I 2 Rt	2.	Q = ∫i2 (t)Rdt		3. i =
						R + r
			0

КОДИ ВІДПОВІДЕЙ ДО ТЕСТУ «Електростатика. Постійний струм»

№	Код	№	Код	№	Код	№	Код	№	Код
питан	відпо	питан	відпо	питан	відпо	питан	відпо	питан	відпо
ня	віді	ня	віді	ня о	віді	ня	віді	ня	віді
1	1	11	1	21	1	31	1	41	4
2	2,4	12	1,3	22	2	32	2	42	2
3	2	13	1,5	23	3	33	4	43	1
4	2	14	2	24	3	34	2	44	2
5	1	15	2	25	2	35	3	45	4
6	1	16	1	26	5	36	3	46	5
7	1	17	4	27	3	37	2	47	−
8	2	18	2,3	28	1	38	1	48	−
9	1	19	3	29	1,4	39	3	49	1,2,4
10	3	20	3	30	3	40	3	50	1,2

170

Електромагнетизм

ЧАСТИНА 4. ЕЛЕКТРОМАГНЕТИЗМ

Розділ 13. Магнітне поле у вакуумі

Магнетизм – особлива форма взаємодії між електричними струмами, між електричними струмами та магнітами і між магнітами. Магнітні властивості характерні в тій чи іншій мірі для всіх без виключення тіл, тому при розгляді магнітних властивостей речовин введено загальний термін – магнетики.

У самому загальному вигляді магнетизм можна визначити як особливу форму матеріальної взаємодії, що виникає між електричне зарядженими частинками, що рухаються. Передача магнітної взаємодії, що реалізує зв’язок, якій відбувається між просторово розділеними тілами, здійснюється магнітним полем. Магнітні поля існують в космічному просторі, вони впливають на рух заряджених частинок, що створюють космічне проміння. Широкий діапазон явищ магнетизму, що тягнеться від магнетизму елементарних частинок до магнетизму космічного простору, обумовлює його велику роль в науці і техніці.

§49 Магнітне поле

49.1Характеристики магнітного поля

В1820 році датський фізик Х. Ерcтед* виявив, що магнітна стрілка, яка розташована паралельно прямолінійному провіднику,

I 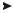N

Рисунок 49.1

Рисунок 49.2

при пропусканні через нього сталого струму I прагне розташуватися перпендикулярно провіднику (рис. 49.1). При зміні напряму струму стрілка поверталася на 180°. Те ж саме відбувалося, коли стрілка переносилася вгору і розташовувалася над дротом.

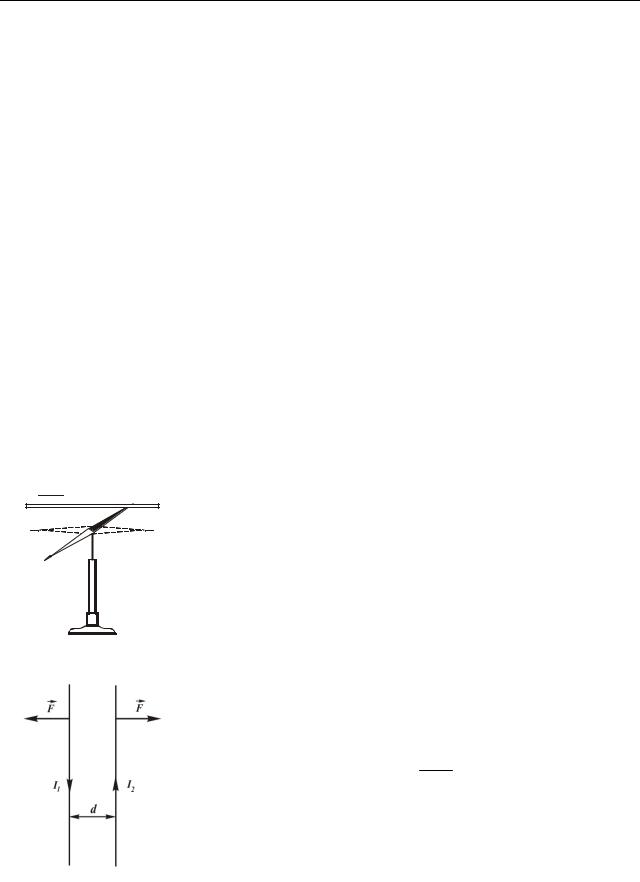
У тому ж році А. Ампер* встановив, що два провідники, які розташовані паралельно один одному, зазнають взаємне тяжіння при пропусканні через них струму в одному напрямі і відштовхуються, якщо струми мають протилежні напрями (рис. 49.2). Сила взаємодії провідників пропорційна величині струмів і обернено пропорційна відстані між ними:

F ~ I1I2 d

Якщо провідник зі струмом помістити між полюсами підковоподібного магніту, то він або втягуватиметься, або виштовхуватиметься з нього залежно від напряму струму (рис. 49.3). Сила дії з боку магнітного поля пропорційна силі струму і довжині провідника:

F ~ I l .

_______________________________________________________________________________

*Эрстед Ханс Крістіан (1777–1851), датський фізик.

*Ампер Андре Марі (1775–1836), французький фізик, математик і хімік.

171

Електромагнетизм

	Таким чином, експерименти показали, що на-
	вколо провідників зі струмом і сталих магнітів існує
	магнітне поле, яке виявляється через силову дію на
	інші провідники зі струмом, сталі магніти, електри-
	чні заряди, що рухаються. На відміну від електрич-
	ного поля магнітне поле не діє на заряд, що покоїть-
	ся.
	Для характеристики здатності магнітного поля
	виявляти силову дію на провідники зі струмом вво-
	диться фізична величина, яка названа вектором ма-
	гнітної індукції.
	Магнітне поле досліджують за допомогою за-
Рисунок 49.3	мкненого контуру зі струмом. Контур повинен мати
	малі розміри в порівнянні з відстанями, на яких маг-

нітне поле помітно змінюється. Це може бути дротяна рамка довільної форми (рис. 49.4 а). Провідники, що підводять, сплітають разом, щоб результуюча сила, що діє на них з боку магнітного поля, дорівнювала нулю.

Розташуємо дріт на відстані, значно більшій за
розміри рамки. Якщо пропускати струм через рамку і
дріт, рамка повертається і розташовується так, що дріт
опиняється в площині рамки (рис. 49.4 б). Як відомо з ку-
рсу механіки, тіло повертається під дією моменту сил.		I0
Якщо брати різні за площею рамки з різними струмами,		I0	I
то моменти сил, що діють на ці рамки в даній точці поля,			I
то моменти сил, що діють на ці рамки в даній точці поля,
будуть різними. Проте відношення максимального моме-	а)	б)
нту сил до добутку сили струму в рамці на її площу буде	а)	б)
для даної точки поля одним і тим же. Це відношення	Рисунок 49.4
приймають як величину, що характеризує магнітне поле, і

називають індукцією магнітного поля в даній точці.

Магнітна індукція ( B ) – це векторна фізична величина, яка є силовою характеристикою магнітного поля і чисельно дорівнює відношенню максимального обертаючого моменту M max , що діє на контур зі струмом в однорідно-

му магнітному полі, до добутку сили струму I в контурі на його площу S:

B =	M max	.	(49.1)

	I S

З дослідів Ампера випливає, що на провідник зі струмом, який розміщений в магнітному поле, діє сила, яка пропорційна струму в провіднику і довжині провідника. Величина сили також залежить від орієнтації провідника в магнітному полі. Виявляється, що відношення максимальної сили, що діє на провідник зі струмом, до добутку сили струму на довжину провідника, для даної точки поля залишається сталим. Тому можна дати інше визначення магнітній індукції.

172

Електромагнетизм

Магнітна індукція ( B ) – це векторна фізична величина, яка є силовою характеристикою магнітного поля і чисельно дорівнює відношенню максимального значення сили Fmax , що діє на провідник зі струмом, до добутку сили

струму I в ньому на довжину провідника l:

							B =	Fmax	.	(49.2)
							B =		.	(49.2)
								I l
[B]=	Н	=	кг м		=	кг	= Тл(тесла* ) .
[B]=	А м	=	А с2		=		= Тл(тесла* ) .
	А м		А с2	м А с2

Окрім вектора магнітної індукції для характеристики магнітного поля ви-

користовують допоміжну величину H , яку називають напруженістю магнітного поля. Магнітна індукція і напруженість зв’язані між собою співвідношенням:

	B = μ0μH ,	(49.3)
де	μ0 = 4π 10−7 Гн/м − магнітна стала;
	μ − відносна магнітна проникність середовища;

H − напруженість магнітного поля.

Магнітна проникність середовища μ − це фізична величина, яка пока-

зує, у скільки разів магнітна індукція поля в даному середовищі відрізняється від магнітної індукції поля у вакуумі. Для вакууму μ=1.

Напруженість магнітного поля H – це векторна величина, яка є кількісною характеристикою магнітного поля. Напруженість магнітного поля визначає той внесок в магнітну індукцію, який дають зовнішні джерела поля.

[H ] = А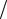м.

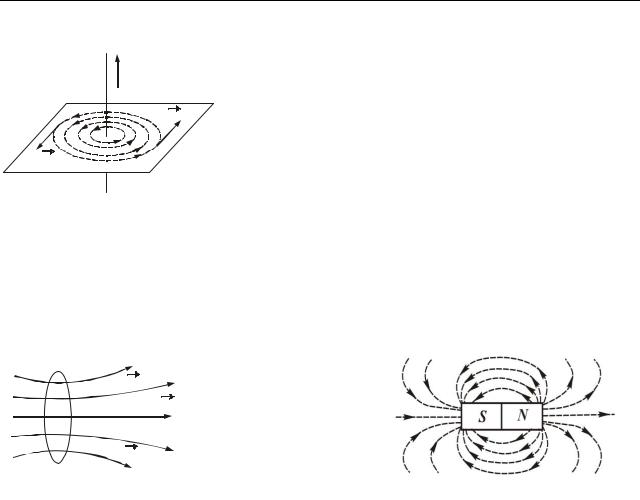
49.2 Графічне зображення магнітних полів

Графічно магнітні поля можна зображати за допомогою ліній магнітної індукції (силових ліній магнітного поля).

Лінія, в будь-якій точці якої вектор магнітної індукції B спрямований по дотичній до неї, називається лінією магнітної індукції (силовою лінією магні-

тного поля).

Силові лінії креслять так, щоб їх густина була пропорційна модулю век-

тора B в даному місці.

Лінії індукції магнітного поля в жодній точці поля не обриваються, тобто вони завжди безперервні. Вони не мають ні початку, ні кінця. Цим силові лінії магнітного поля відрізняються від силових ліній електростатичного поля, які завжди починаються і закінчуються на електричних зарядах або йдуть в нескінченність. Векторне поле, що має безперервні силові лінії, називається вихровим полем. Магнітне поле – це вихрове поле.

________________________________________________________________________________

*Тесла Никола (1856−1943), американський учений, фізик, інженер. Серб за походженням.

173

Електромагнетизм

Лінії індукції прямого провідника із струмом є колами, що лежать в площині, перпендикулярній до провідника. Центри кіл

	I	знаходяться на осі провідника (рис. 49.5) Напрям
	B	ліній індукції магнітного поля визначається за
	B	мнемонічним правилом буравчика: напрям ліній ін-
	B	дукції співпадає з напрямом ручки буравчика, який
	B	угвинчують уподовж напрями струму.
		Лінії індукції кругового струму представлені
	Рисунок 49.5	на рис. 49.6. Лінії індукції поля, створюваного по-
	Рисунок 49.5	стійним магнітом – на рис. 49.7.
		стійним магнітом – на рис. 49.7.

Якщо у всіх точках деякої частини простору вектор магнітної індукції B не змінює свого напряму і чисельного значення, те магнітне поле в цій частині простору називається однорідним. У протилежному випадку магнітне поле є неоднорідним.

I B

Рисунок 49.6

Рисунок 49.7

§50 Розрахунок магнітних полів. Закон Біо − Савара − Лапласа

50.1Закон Біо − Савара − Лапласа

У1820 році французькі вчені Біо* і Савар* провели дослідження магнітних полів струмів, що протікали по тонким провідникам різної форми. Лаплас* проаналізував експериментальні дані і отримав співвідношення, яке дозволяє

визначити магнітну індукцію dB поля,		створюваного елементом струму. Під
елементом струму розуміють добуток струму I на елемент довжини dl			провід-
ника.
Згідно із законом Біо − Савара − Лапласа індукція dB магнітного поля,
створюваного елементом струму	Idl в довільній точці А, визначається вира-
зом:
dB	= μ0μ	Idl sin α ,	(50.2)
	4π	r2

________________________________________________________________________________

*Био Жан Батист (1774–1862), французький фізик. *Савар Фелікс (1791–1841), французький фізик.

*Лаплас Пьер Симон (1749–1827), французький астроном, математик і фізик.

174

Електромагнетизм

де α − кут між напрямами елемента струму і радіус-вектора rr, що йде від

I	елемента струму до точки, в якій визначається індукція
dB	(рис. 50.1).
dB	Аналогічні формули можна записати для напру-
A	женості магнітного поля:	Idl ×rr
r	r	Idl ×rr	,	(50.3)
Idl	dH =	4πr3	,	(50.3)
		4πr3

Рисунок 50.1	dH =	Idl sin α .		(50.4)
Рисунок 50.1		4πr2

Магнітне поле будь-якого струму може бути обчислено як векторна сума полів, створюваних елементарними ділянками струмів:

Br = ∫dBr.

Якщо магнітне поле створюється системою провідників із струмами, то індукція результуючого поля в будь-якій його точці дорівнює векторній сумі індукцій магнітних полів, створюваних кожним струмом окремо:

Br = B1 + B2 +... + Bn .

Це твердження носить назву принципу суперпозиції полів.

Застосуємо закон Біо − Савара − Лапласа для розрахунку полів, створюваних провідниками правильної геометричної форми у вакуумі.

50.2Приклади розрахунку магнітних полів

1.Поле прямого струму. Всі елементи струму прямолінійного провідника

дають співспрямованіr вектори dB (для наведеного на рис. 50.2 напряму струму вектори dB направлені перпендикулярно до площини креслення до нас). Векторне складання можна замінити скалярним:

dl 1 r d

N 2

Рисунок 50.2

B = ∫dB = ∫		μ	0	I dl sin α		.	(50.5)
				4πr	2
l	l

Приведемо підінтегральний вираз до однієї змінної α . З рис. 50.2 випливає, що

r =	r0	,	dl =	rdα	=	r0dα	.
	sin α			sin α		sin2 α

Отримані вирази підставимо у формулу (50.5):

175

Електромагнетизм

α2

μ I

r dαsin3 α

α2

μ I

B = ∫

40π

= ∫

sin αdα.

sin

αr

4πr

α1

Інтегрування дає співвідношення:

B =

μ0 I

(cos α − cos α

(50.6)

4πr0

Кути α1 і α2 позначені на рис. 50.2.

Розглянемо провідник нескінченної довжини. Практично це виконується за умови r0 << l . Отримаємо вираз для індукції магнітного поля, створюваного

нескінченно довгим провідником. У цьому випадку можна вважати, що α1 = 0 ,

α2 = π	μ0 I				μ0 I
B =	μ0 I	(cos 0 − cos π)=			μ0 I	2 ,
B =	4πr	(cos 0 − cos π)=			4πr	2 ,
	4πr				4πr
тобто	0				0
тобто			μ0 I
		B =	μ0 I	,		(50.7)
		B =	2πr	,		(50.7)
			2πr
			0

де r0 − відстань від провідника із струмом до точки, в якій визначається магніт-

на індукція.

Аналогічну формулу можна записати для напруженості магнітного поля:

H =	I	.	(50.8)
H =	2πr	.	(50.8)
	2πr
	0

2. Поле кругового струму на його осі. Знайдемо індукцію магнітного поля B в точці А, розташованої на осі кругового струму радіусу R, на відстані x від його центру (rрис. 50.3).

Індукція dB поля, створеного елементом струму Idl , згідно із формулою

(50.2):

	dl				dB =	μ0	Idl sin α .
Idl	dl		r	dB dB		4π	r2
			r	Розкладемо вектор		dB	на дві складові: dBII −
I	R			Розкладемо вектор		dB	на дві складові: dBII −
	0	x		A dB x направлену вздовж осі 0x і dB − перпендикуля-
				рну до неї.
		Рисунок 50.3
				Br = ∫dBrII + ∫dBr .
				l	l

176

Електромагнетизм

r При підсумовуванні полів всіх елементів струму по довжині кола складові dB в сумі дадуть нуль, тобто

∫dB = 0 .

Вектори dBrII співнаправлені, тому векторну суму замінимо скалярною:

B = ∫dBII = ∫dB sin β.

	l	l
З рис. 50.3 знаходимо
r2 = R2 + x2 ,		sin β =	R =		R	.
			r		R2 + x2
Підставивши отримані співвідношення і враховуючи, що						sin α =1, маємо:
dB =	μ0	Idl R		.
dB =	4π	(R2 + x2 )3 2		.

Інтегруючи по dl і враховуючи те, що			∫dl = l = 2πR , отримаємо:
			l
B = ∫	μ0	IdlR		=	μ0 I 2πR2	,
			3 2		3 2
l	4π	(R2 + x2 )			4π(R2 + x2 )

B =	μ0 I R2
		.
	2 (R2 + x2 )3 2

Аналогічну формулу можна записати для напруженості магнітного поля:

H =	IR2
		.
	2(R2 + x2 )3 2

(50.9)

(50.10)

При x =0 отримаємо вираз для розрахунку індукції в центрі кругового струму:

B =	μ0 I	.	(50.11)

	2R

Напруженість магнітного поля в центрі кругового струму:

H =	I	.	(50.12)

	2R

177

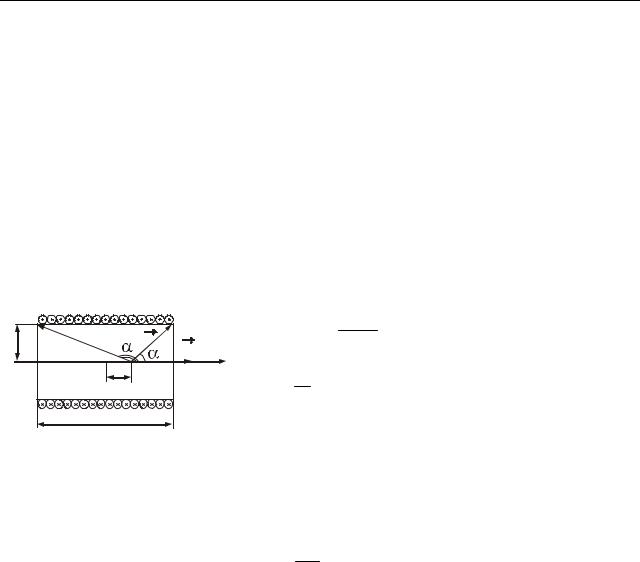
Електромагнетизм

3.Поле соленоїда кінцевої довжини. Соленоїд є дротом, закрученим на круглий циліндричний каркас. На рис. 50.4 показано переріз соленоїда. Магніт-

на індукція B поля соленоїда кінцевої довжини дорівнює геометричній сумі магнітних індукцій Bri полів всіх витків цього соленоїда:

r	N	r
B = ∑Bi			,	(50.13)
	i =1		i

Усередині соленоїда напрям індукції B співпадає з напрямом осі. Використовуючи формули (50.9) і (50.13), можна отримати формулу для

розрахунку індукції магнітного поля в довільній точці А, що лежить на осі соленоїда кінцевої довжини:

B = μ0 In (cos α − cos α

(50.14)

x A

n =

− число витків на одиницю довжини со-

де

леноїда (густина намотування);

Рисунок 50.4

α1

і α2

− кути, під якими з точки А видні кінці

соленоїда (рис. 50.4).

Напруженість магнітного поля в довільній точці на осі соленоїда кінцевої

довжини

H =

I n (cosα − cosα

(50.15)

У вченні про електромагнетизм велику роль грає уявний нескінченно довгий соленоїд. Причина цього полягає в тому, що поле такого соленоїда однорідне і обмежено об’ємом соленоїда (аналогічно електричне поле нескінченного плоского конденсатора однорідне і обмежено об’ємом конденсатора). Соленоїд вважається нескінченно довгим, якщо l >> R . Для нескінченно довгого соленоїда α1 = 0 , α2 = π. Тоді:

B =	μ0 I n	(cos 0 −cos π)=	μ0 I n	2 = μ0I n .
B =	2	(cos 0 −cos π)=	2	2 = μ0I n .
	2		2
		B = μ0 I n .		(50.16)

Відповідно, напруженість магнітного поля усередині нескінченно довгого соленоїда:

H = I n .

(50.17)

178

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1718 / 2318 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
03.03.2016577.54 Кб15МУ_ПУ.doc
#
03.03.2016909.97 Кб33МУ_ТОБ_2013_БС_ТТР.pdf
#
03.03.20162.07 Mб205Навчальний посибник.pdf
#
03.03.20161.98 Mб151навчатьный посибник 2.pdf
#
03.03.2016177.15 Кб4налоги.docx
#
03.03.20163.85 Mб118Научное помсобие 1All Tom 1 UA.pdf
#
03.03.20163.77 Mб174Научный пособник том 2All Tom 2 UA.pdf
#
03.03.201614.29 Mб48НГ_МУ_6_35.pdf
#
03.03.201629.11 Кб63Нетрадиционные источники энергии.docx
#
03.03.2016497.27 Кб3НИРС -ВИКА -2.3(23.09).docx
#
03.03.201656.21 Кб3НИРС.docx