Научное помсобие 1All Tom 1 UA

Вступ

ПЕРЕДМОВА

Пропонований навчальний посібник написаний відповідно до програми курсу «Фізика» для інженерно-технічних спеціальностей вищих навчальних закладів. Зміст першого тому складають розділи: фізичні основи механіки, молекулярна фізика і термодинаміка, електростатика і постійний струм, електромагнетизм. Зміст другого тому: коливання і хвилі, хвильова і квантова оптика, елементи квантової механіки, основи фізики твердого тіла, елементи фізики атомного ядра.

Основна мета посібника – допомогти студентам вивчити курс фізики. Автори намагалися з одного боку максимально повно охопити всі розділи курсу, що передбачені програмою, а з іншого – викласти весь матеріал компактно, не використовуючи громіздких математичних викладень, просторових міркувань й ін. Основну увагу надано суті даних явищ, законам, що описують ці явища, межам застосовності законів, а також визначенням фізичних величин, одиницям вимірювання. Визначення, формулювання законів, а також всі нові терміни виділені в тексті курсивом. Математичні знання, необхідні для користування допомогою, відповідають звичайному курсу математики у вищому технічному навчальному закладі.

Зведені таблиці, що наведені в тексті, а також велика кількість посилань і ілюстрацій допоможуть вам краще зрозуміти і засвоїти навчальний матеріал, а тести – перевірити рівень засвоєння матеріалу.

Вивчення матеріалу рекомендуємо проводити у два етапи:

1)швидке читання матеріалу всієї теми з метою ознайомлення з його структурою, виділенням основних питань;

2)читання з опрацьовуванням: на цьому етапі треба зрозуміти весь

матеріал.

Вивчаючи курс фізики, пам’ятайте, що деяка частина навчального матеріалу підлягає обов’язковому запам’ятовуванню. Це визначення, формулювання законів, одиниці вимірювання фізичних величин. Щоб глибше зрозуміти суть явищ, навчитися застосовувати закони, що описують ці явища, необхідно розв’язувати задачі. Уміння розв’язувати задачі – головний критерій оцінки засвоєння навчального матеріалу. Експериментальні задачі, методи обробки результатів і їх уявлення, а також правила поводження з найпростішими приладами розглядаютьсяу фізичному практикумі.

Автори виражають глибоку подяку рецензентам: проф. Голубничому П.І. завідувачеві кафедри фізики Східноукраїнського університету ім. Володимира Даля; доц. Русакову В.Ф. завідувачеві кафедри загальної фізики і дидактики фізики Донецького національного університету; проф. Тарасенку С.В. завідувачеві відділу теорії магнетизму і фазових переходів Донецького фізико-технічного інституту ім. О.О. Галкіна НАН України; Русаковій Н.М. старшому викладачу кафедри фізики Донецького національного технічного університету за корисні зауваження і поради, які були враховані під час підготовки рукопису до друку. Також виражаємо свою подяку і вдячність Лумпієву І.В. за оформлення графічного матеріалу книги.

Із зауваженнями і пропозиціями щодо книги до авторів можна звернутися електро-

нною поштою: afv.@fizmet.dgtu.donetsk.ua

9

Вступ

ВСТУП

§1 Предмет фізики

Фізика – це наука, що вивчає найпростіші і разом з тим найзагальніші закономірності явищ природи, властивості і будову матерії, закони її руху.

В даний час відомі два види неживої матерії: речовина і поле. До першого виду матерії – речовини – відносяться атоми, молекули і всі тіла, що складаються з них. Другий вид матерії утворюють гравітаційні, електромагнітні та інші поля.

Матерія знаходиться в безперервному русі, під яким розуміється будь-яка зміна взагалі. Рух є невід’ємною властивістю матерії, яка є нествореною і незнищенною, як і сама матерія. Матерія існує і рухається в просторі і в часі.

Основним методом дослідження у фізиці є експеримент (дослід), тобто спостереження досліджуваного явища в точно контрольованих умовах, що дозволяють стежити за ходом дослідження і відтворювати його кожного разу при повторенні цих умов.

Для пояснення фізичних явищ використовують гіпотези. Гіпотеза – це наукове припущення, що висувається для пояснення певного факту або явища і вимагає перевірки і доказу. Правильність гіпотези перевіряється постановкою відповідних дослідів, через з’ясування узгодження наслідків, що випливають з гіпотези, з результатами дослідів і спостережень. Доведена гіпотеза перетворюється на наукову теорію або закон.

Фізична теорія – це система основних ідей, що узагальнюють дослідні дані і відображають об’єктивні закономірності природи. Фізична теорія дає пояснення всій сфері явищ природи з єдиної точки зору.

Фізика є науковим фундаментом розвитку нових галузей техніки. На основі її відкриттів створена електротехніка і радіотехніка, електронна й обчислювальна техніка, космічна техніка і приладобудування, ядерна енергетика, лазерна техніка та ін. На основі досягнень фізики розробляються принципово нові і досконаліші методи виробництва, прилади і установки. У свою чергу техніка, розвиваючись і удосконалюючись, висуває перед фізикою такі проблеми, вирішення яких вимагає більш глибокого вивчення різних фізичних явищ. Саме технічні потреби спонукали суспільство свого часу до розвитку механіки, необхідної для будівництва різних споруд. Необхідність створення більш економічних двигунів зумовила бурхливий розвиток термодинаміки і т.д.

Фізика формує науковий світогляд людини. Розвиваючись, вона видозмінює, доповнює, поглиблює уявлення про природу речей і причинні зв’язки навколишнього світу. З часом її теоретичні концепції набувають загально філософського значення. Таким чином, інженер будь-якого профілю повинен володіти фізикою в такій мірі, щоб бути в змозі застосовувати її досягнення у своїй виробничій діяльності.

10

Вступ

§2 Загальні відомості

1.Реальні властивості матеріальних об’єктів настільки складні, а взаємні зв’язки між явищами такі різноманітні, що врахувати всі ці властивості і зв’язки відразу неможливо. Тому в процесі пізнання необхідно виділяти в об’єктах, що вивчаються, головне, істотне і відволікатися від усього випадкового, другорядного.

Операція, в ході якої головне відділяється від другорядного, називається абстрагуванням. Побудована в результаті абстрагування ідеалізована, спрощена схема явища або об’єкту, називається фізичною моделлю. Прикладами фізичних моделей є матеріальна точка, абсолютно тверде тіло, ідеальний газ, рівноважний процес, точковий заряд, елемент струму, абсолютно чорне тіло тощо.

Будь-яка фізична модель має обмежений характер і придатна лише для наближеного опису явища і об’єкту. Отже, закономірності, отримані на основі фізичних моделей, також мають наближений і обмежений характер. Завжди є принципова можливість уточнення, доповнення, узагальнення того або іншого закону. Проте встановлені на певному етапі розвитку фізики закономірності, що правильно пояснюють експериментальні дані, не відкидаються з розвитком нового етапу, а включаються до нього, як граничний випадок, справедливий у певних умовах. Таким чином, завжди має виконуватися принцип відповідності.

2.Всі поняття і фізичні моделі вводяться в науку за допомогою визначень, які дозволяють створити єдину наукову термінологію. Визначення – це сформульований в стислій формі зміст поняття. У всіх наукових теоріях є поняття, які приймаються без визначень. У фізиці без визначень приймаються такі поняття, як стан, явище, процес, взаємодія та ін.

Основними фізичними поняттями є фізична величина і фізичний закон. 2.1. Фізична величина – це характеристика однієї з властивостей фізич-

ного об’єкту або фізичного явища, яку можна прямо або побічно зміряти і виразити числом.

В якісному відношенні ця величина властива багатьом об’єктам, в кількісному відношенні – індивідуальна. Наприклад, будь-яке фізичне тіло можна характеризувати масою, але чисельне значення маси у кожного тіла своє.

У визначенні фізичної величини необхідно відображати її якісний і кількісний зміст. Відобразити якісний зміст – означає вказати, яку властивість або процес характеризує величина. Наприклад, опір провідника характеризує здатність провідника перешкоджати проходженню струму; електроємність провідника характеризує здатність провідника накопичувати електричний заряд.

Відобразити кількісний зміст – означає вказати спосіб вимірювання цієї величини. Наприклад, електроємність – це величина, що чисельно дорівнює заряду, який потрібний для зміни потенціалу провідника на один вольт.

Фізичні величини можуть бути скалярними або векторними, тому у визначенні також необхідно вказувати характер величини. Наведемо як приклад повне визначення електроємності.

11

Вступ

Електрична ємність (електроємність) – це скалярна фізична величина, що характеризує здатність провідника накопичувати електричний заряд і чисельно дорівнює заряду, який потрібний для зміни потенціалу провідника на один вольт:

C = ϕq .

Не всі поняття, що розглядаються у фізиці, є фізичними величинами. Не є фізичними величинами система відліку, матеріальна точка, рівноважний процес та ін.

2.2. Фізичний закон – це знайдена на досліді або встановлена теоретично, шляхом узагальнення дослідних даних, кількісна або якісна об'єктивна залежність одних фізичних величин від інших.

Кількість фундаментальних законів природи, відомих у наш час, порівняно невелике і виражаються вони з математичної точки зору, як правило, просто. Набагато більш обширно і вимагають більш серйозного математичного апарату окремі випадки прояву законів. Використовуючи правила поводження з математичними величинами, можна отримати численні наслідки, що допускають експериментальну перевірку.

Не слід плутати визначення фізичної величини з фізичним законом. Наприклад, густина твердого тіла за визначенням дорівнює

ρ = Vm .

Не можна говорити, що густина – це величина, пропорційна масі тіла і обернено пропорційна його об’єму, оскільки у твердих тіл не можна змінити масу, не змінивши його об’єм.

3. Одиницею виміру фізичної величини називається умовно обрана фізи-

чна величина, що має той же фізичний сенс, що розглядається. Системою одиниць називається сукупність одиниць фізичних величин, що відноситься до певної системи величин і утворена відповідно до певних правил. Основними одиницями цієї системи називаються одиниці декількох різнорідних фізичних величин, що довільно обрані при побудові цієї системи. Похідними одиницями називаються одиниці, встановлювані через інші одиниці цієї системи на підставі фізичних законів, які виражають взаємозв’язок між відповідними фізичними величинами.

Стандартом встановлено, що обов’язковому застосуванню підлягають одиниці Міжнародної системи одиниць (СІ), а також десяткові кратні і часткові від них. Основними одиницями СІ є: метр (м) – одиниця довжини; кілограм (кг)

– одиниця маси; секунда (с) – одиниця часу; ампер (А) – одиниця сили струму; кельвін (К) – одиниця термодинамічної температури; кандела (кд) – одиниця сили світла; моль (моль) – одиниця кількості речовини. Додаткові одиниці СІ: радіан (рад) – одиниця плоского кута; стерадіан (ср) – одиниця тілесного кута.

12

Вступ

У деяких областях науки і техніки допускається використовування позасистемних одиниць. Наприклад, в ядерній фізиці масу виміряють в атомних одиницях маси (а.о.м.), а енергію – в електрон-вольтах (еВ).

Докладну інформацію про одиниці вимірювання можна знайти в довідкових матеріалах.

4. Мовою фізики є математика, зокрема диференціальне і інтегральне числення. Застосовуючи апарат вищої математики, фізика вкладає дещо інше значення в деякі її поняття. Поняття «елементарна фізична величина», що використовується у фізиці не можна ототожнювати з поняттям математично нескінченно малої величини.

Наприклад, елементарний об’єм dV – це такий об’єм, який, з одного боку, такий великий, що містить достатньо велику для того або іншого усереднювання кількість частинок; з іншого боку, настільки малий, що дана макроскопічна величина, наприклад густина, у всіх його точках залишається однаковою, навіть якщо вона змінюється в даному макроскопічному об’ємі V.

§3 Основні відомості про вектори

Скалярні і векторні величини. Величини, значення яких задаються позитивними або негативними числами, називають скалярними (маса, температура, робота і т.п.). Величини, значення яких визначаються як числом, так і напрямом у просторі, називаються векторними (сила, швидкість, прискорення, напруженість електричного і магнітного поля і т.п.), і можуть бути зображені векторами.

їх модулі і співпадають напрями (тобто вектори паралельні і орієнтовані в одну сторону).

співпадає з початком координат, а кінець знаходиться в точці М (рис. 3.1) цілкомr визначає цю точку і називається радіус-вектором точки М. Позначається r . Точка 0 у цьому випадку називається полюсом.

Лінійні комбінації векторів. Сума двох векторів a і b є вектор cr, який є діагоналлю АС паралелограма ABCD (рис. 3.2).

13

Вступ

m>0 і протилежний йому при m<0.

Кожний вектор arrу просторі може бути розкладений на суму векторів, паралельних ортам i , j , k :

ar = i ax + jay + kaz ,

де ах, ау, az – проекції вектора ar на відповідні координатні осі.

Скалярне множення векторів. Скалярним добутком векторів ar і b нази-

вається скаляр, що визначається рівністю

arb = abcosϕ,

де ϕ – кут між векторами ar і b , приведеними до загального початку (позначення див. рис. 3.3).

14

Вступ

Таблиця 3.1

Властивості добутків векторів

Скалярні і векторні поля. Градієнт

Скалярним полем називається область простору, кожній точці якої віднесено значення певної скалярної величини ϕ = ϕ(x, y, z) . Таким полем є, напри-

клад, поле температури нерівномірно нагрітого тіла, поле густини неоднорідного тіла, поле електростатичного потенціалу і т.п.

Векторним полем називається область простору, кожній точці якої віднесено значення певного вектора. Таким полем, наприклад, єrполе вектора напруженості електричного поля E , вектора магнітної індукції B .

15

Вступ

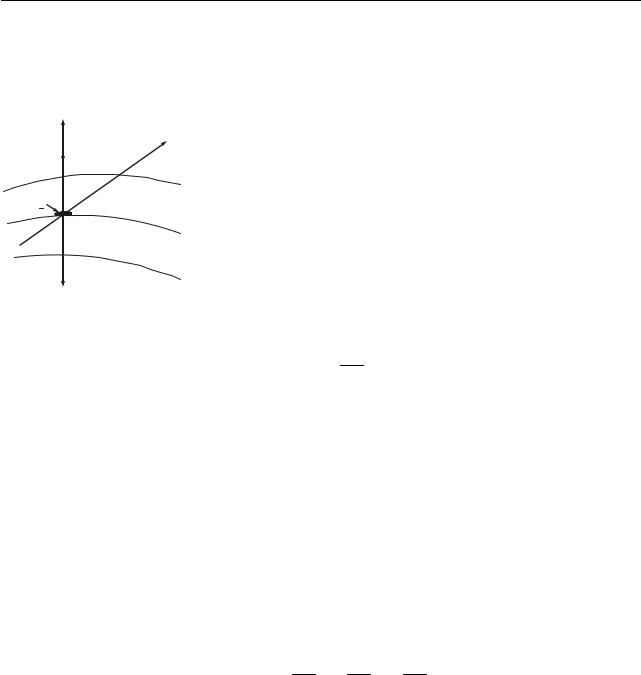
Градієнт скалярної величини – це вектор, направлений у бік максимального зростання цієї величини і чисельно рівний зміні величини, що припадає на одиницю довжини в цьому напрямі.

самі на себе, або закінчуються на межі тіла. Зміна температури в довільному напрямі l

характеризується похідною за напрямом ∂∂Tl . Ця похідна матиме максимальне

значення у напрямі нормалі до ізотермічної поверхні (в нашому випадку це напрям х). Вектор, направлений по нормалі до ізотермічної поверхні у бік зростання температури, називається градієнтом температури і позначається gradT :

Чисельно градієнт температури дорівнює різниці температур двох точок віддалених одна від однієї на одиницю довжини.

Якщо ввести декартові систему координат, то градієнт температури може бути виражений співвідношенням:

grad T = ir∂∂Tx + rj ∂∂Ty + kr∂∂Tz ,

де ir, rj , k − одиничні вектори (або орти).

Звертаємо увагу на те, що поняття градієнта різних величин дуже широко використовується у фізиці, і ми будемо до нього не раз звертатися.

16

Фізичні основи механіки

ЧАСТИНА 1. ФІЗИЧНІ ОСНОВИ МЕХАНІКИ

Найпростішою формою руху є механічний рух, що полягає в зміні положення тіла з часом відносно інших тіл або частин одного і того ж тіла.

Розділ фізики, що вивчає закономірності механічного руху і взаємодії тіл, називається механікою. Рух тіл із швидкостями, багато меншими за швидкість світла с у вакуумі, вивчає класична механіка. В основі класичної механіки лежать закони динаміки, сформульовані İ. Ньютоном* в 1687 році. Закони Ньютона виникли в результаті узагальнення великої кількості дослідних фактів.

З розвитком науки виявилися нові факти, які не вкладалися в межі класичної механіки. Вони отримали пояснення в теорії відносності і в квантовій механіці.

Теорія відносності, сформульована А. Ейнштейном* в 1905 році, переглянула ньютонівські уявлення про простір і час. В результаті була створена механіка тіл, що рухаються із швидкостями, близькими до швидкості світла у вакуумі – релятивістська механіка. Рівняння релятивістської механіки у граничному випадку (для швидкостей малих порівняно із швидкістю світла) переходять в рівняння класичної механіки. Таким чином, класична механіка увійшла до релятивістської механіки як граничній випадок і зберегла своє колишнє значення для опису руху тіл з малими швидкостями.

В результаті розвитку фізики атома у 20-х роках двадцятого століття була створена квантова механіка. Рівняння квантової механіки також дають у граничному випадку (для мас, великих порівняно з масами атомів) рівняння класичної механіки. Отже, класична механіка увійшла і до квантової механіки як граничний випадок. Таким чином, розвиток науки не перекреслив класичну механіку, а лише показав її обмежену застосовність.

Класична механіка складається з трьох розділів: кінематики, динаміки і статики. Кінематика математично описує різні види механічного руху, не з’ясовуючи причин цього руху. Динаміка досліджує вплив взаємодії між тілами на їх механічний рух. Статика вивчає умови рівноваги тіл. Закони статики є окремим випадком законів динаміки, тому в даному курсі статику ми розглядати не будемо.

Розділ 1. Кінематика поступального і обертального руху

§4 Кінематика матеріальної точки

4.1 Основні поняття кінематики

Для опису реальних тіл, що рухаються, в механіці залежно від умов конкретної задачі користуються різними фізичними моделями, а саме: матеріальна точка, абсолютно тверде тіло, абсолютно пружне тіло, абсолютно непружне тіло.

________________________________________________________________________________

*Ньютон İсаак (1642–1727), англійський фізик, математик і астроном.

*Ейнштейн Альберт (1879–1955), німецький фізик, лауреат Нобелівської премії 1921 р.

17

Фізичні основи механіки

Матеріальною точкою називається тіло, розмірами якого в умовах даної задачі можна знехтувати. Наприклад, при дослідженні руху автомобіля з одного пункту в інший, його можна вважати матеріальною точкою. Якщо ви вивчаєте рух водія, що знаходиться всередині автомобіля, то автомобіль треба розглядати як протяжне тіло.

Абсолютно твердим тілом називається тіло, деформацією якого в умовах даної задачі можна знехтувати. Абсолютно тверде тіло можна розглядати як систему матеріальних точок, жорстко зв’язаних між собою.

Абсолютно пружним тілом називається тіло, яке після припинення зовнішньої силової дії повністю відновлює свої первинні розміри і форму.

Абсолютно непружним тілом називається тіло, яке після припинення зовнішньої силової дії повністю зберігає деформований стан, зумовлений цією дією.

4.2 Система відліку. Траєкторія. Шлях. Переміщення

Положення тіла в просторі завжди вказується відносно інших тел. Тіло, відносно якого розглядається рух, називається тілом відліку. Щоб визначити положення досліджуваного тіла, з тілом відліку жорстко пов’язують систему

Лінія, описувана в просторі точкою, що рухається, називається траєкторією. Залежно від виду траєкторії рух поділяють на прямолінійний і криволінійний. Окремим видом криволінійного руху є рух по колу.

Нехай матеріальна точка, рухаючись по деякій траєкторії (рис. 4.1), перемістилася з точки 1 в точку 2. Відстань S12 між точками 1 і 2, відлічена вздовж

Вектор, що сполучає початкове і кінцеве положення точки, називається переміщенням і позначається r (рис. 4.2).

4.3 Способи завдання положення тіла в просторі

Основна задача кінематики – визначення положення тіла у будь-який момент часу. Звичайно положення тіла визначають за допомогою координат. Рух точки вважається повністю визначеним, якщо задані рівняння, що описують зміну координат точки з часом:

Ці рівняння називаються кінематичними рівняннями руху точки.

18