
- •Державний вищий навчальний заклад донецький національний технічний університет
- •Логіка та методи наукових досліджень
- •Інформаційне забезпечення наукових досліджень
- •Гіпотези і доведення у наукових дослідженнях
- •Двовибіркові t-тести Стьюдента
- •Методологічні основи статистичного моделювання та прогнозування
- •Моделювання та прогнозування динаміки
- •Основи моделювання взаємозв’язків
- •Множинна регресія в соціально-економічних дослідженнях
- •Моделювання причинних комплексів
- •Науковий результат: зміст і порядок оформлення
Основи моделювання взаємозв’язків
Основні засади аналізу кореляційних зв'язків
У процесі дослідження розв'язується триєдина задача:
встановлюється факт наявності зв'язку між явищами, його напрямок і форми;
вимірюється ступінь щільності зв'язку;
• оцінюються ефекти впливу одних явищ на інші.
Для соціально-економічних явищ характерні переважно кореляційні зв'язки, які через складність взаємодії факторів і вплив випадкових причин проявляються не в кожному окремому випадку, а лише в середньому. За напрямом впливу кореляційні зв'язки бувають прямими і зворотними, за аналітичною формою - лінійними і нелінійними, за кількістю взаємодіючих факторів - парними і множинними.
Найпростішою системою кореляційного зв'язку є парна кореляція, коли одне явище розглядається як фактор, інше - як результат. Відповідно ознаки, що характеризують ці явища, називаються: факторною х і результативною у. Наявність зв'язку між ними має бути попередньо обґрунтована і представлена у вигляді гіпотези.
Виявити узгодженість (неузгодженість) варіації двох ознак можна за допомогою паралельних рядів, коли одиниці сукупності упорядковуються за значеннями факторної ознаки х, а паралельно розміщуються відповідні їм значення результативної ознаки у. Наявність чи відсутність зв'язку виявляється зіставленням паралельних рядів.
Форму кореляційного зв'язку між ознаками можна описати аналітично у вигляді функції У = f(х), яка називається регресією у по х. У лінійному щодо параметрів рівнянні регресії індивідуальне значення результативного показника уj (де j — порядковий номер одиниці сукупності) записується так:
 ,
,
де b0 — вільний член рівняння; економічного змісту, як правило, не має, лише окреслює область існування моделі;
bі — коефіцієнт регресії; показує, як в середньому змінюється у зі зміною хі на одиницю її шкали вимірювання за незмінності інших включених в модель факторів і за інших рівних умов;
ej = yj – Yj — залишкова величина.
У регресійній моделі основне навантаження покладається на коефіцієнт регресії bі, він розглядається як своєрідна міра «очищеного» впливу хі на у і називається ефектом впливу.
Коефіцієнт регресії розглядається як ефект впливу х на у. У парній лінійній регресії сума квадратів відхилень мінімізується при таких значеннях параметрів а та b:
 ,
или
,
или
 ;
;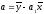
Параметри рівняння регресії визначаються методом найменших квадратів (МНК), основна умова якого - мінімізація суми квадратів відхилень емпіричних значень уj від теоретичних
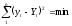 .
.
де j - порядковий номер одиниці сукупності.
Відхилення
 пояснюються
впливом інших, не включених у модель
факторів, називаютьсязалишками
і
позначаються ej.
пояснюються
впливом інших, не включених у модель
факторів, називаютьсязалишками
і
позначаються ej.
У невеликих за обсягом сукупностях коефіцієнт регресії схильний до випадкових коливань, тому слід перевірити його істотність. При лінійному зв'язку істотність коефіцієнта регресії перевіряють за допомогою t-критерію Стьюдента, статистична характеристика якого для гіпотези Н0:b = 0 визначається відношенням коефіцієнта регресії b до власної стандартної похибки μb, тобто
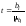 ,
,
Стандартна похибка коефіцієнта регресії залежить від варіації факторної ознаки х, залишкової дисперсії Se2 і числа ступенів свободи df =n-m, де т- кількість параметрів рівняння регресії (для лінійної регресії т =2):

Для
коефіцієнта регресії, як і для будь-якої
іншої випадкової величини,
визначаються довірчі межі.
 ,
,
Мірою щільності парного лінійного зв'язку слугує коефіцієнт кореляції r
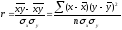
Оскільки
факторні ознаки мають, як правило, різні
одиниці вимірювання, то для порівняння
ефектів їх впливу в рамках моделі
використовують стандартизовані
коефіцієнти регресії
 (бета-коефіцієнти) або коефіцієнти
еластичності
(бета-коефіцієнти) або коефіцієнти
еластичності
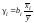 .Бета-коефіцієнт
характеризує ефект впливу хі
на у
в середньоквадратичних відхиленнях,
коефіцієнт
еластичності
— в процентах.
.Бета-коефіцієнт
характеризує ефект впливу хі
на у
в середньоквадратичних відхиленнях,
коефіцієнт
еластичності
— в процентах.
Для оцінювання адекватності регресійної моделі використовують:
стандартне відхилення;
множинні коефіцієнти детермінації та кореляції;
частинні коефіцієнти детермінації та кореляції;
коефіцієнти окремої детермінації;
критерії перевірки істотності зв’язку.
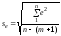
Стандартне відхилення характеризує варіацію залишкових величин
 ,
,
де n — обсяг сукупності, m — кількість коефіцієнтів регресії.
Розрахунок характеристик щільності зв’язку ґрунтується на декомпозиції (розкладанні) варіації у за джерелами формування:
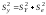 ,
,
де
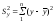 —загальна
сума квадратів відхилень,
зумовлена впливом усіх можливих факторів;
—загальна
сума квадратів відхилень,
зумовлена впливом усіх можливих факторів;
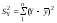 —факторна
сума квадратів відхилень,
зумовлена впливом включених у модель
факторних ознак хі;
—факторна
сума квадратів відхилень,
зумовлена впливом включених у модель
факторних ознак хі;
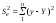 —
залишкова
сума квадратів відхилень,
розмір
якої залежить від потужності впливу не
включених у модель факторів.
—
залишкова
сума квадратів відхилень,
розмір
якої залежить від потужності впливу не
включених у модель факторів.
Відношення факторної суми квадратів до загальної характеризує частку варіації у, пов’язану з варіацією включених у модель факторів, і називається множинним коефіцієнтом детермінації
 .
.
Коефіцієнт детермінації характеризує частку варіації результативної ознаки у, яка пов'язана з варіацією фактору х. За відсутності зв'язку R2=0. Якщо зв'язок функціональний, R2=1.
Корінь квадратний із коефіцієнта детермінації називають коефіцієнтом кореляції. Якщо зв'язок лінійний, то R =|r|. Перевірка істотності кореляційного зв'язку ґрунтується на порівнянні фактичних значень R2 з критичними, які могли б виникнути за відсутності зв'язку. Якщо фактичне значення R2 перевищує критичне, то зв'язок між ознаками не випадковий. Гіпотеза, що перевіряється, формулюється як нульова: Н0 : R2 = 0 .
Критичні значення характеристик щільності зв'язку для рівня істотності а = 0,05 і відповідного числа ступенів свободи наведено в табл. 4.4.2. Число ступенів свободи df залежить від обсягу сукупності n і кількості параметрів рівняння т. Для факторної дисперсії df дорівнює (т - 1), для залишкової - (п - т).
Розглянута
процедура перевірки істотності зв'язку
є складовою дисперсійного аналізу (див.
4.3).
 або
або
 .
.
Критичні
значення
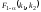 ,
де α — рівень істотності, k1 = m – 1,
k2 = n – (m – 1) — числа
ступенів вільності чисельника та
знаменника, наведено в додатку 10. Оскільки
F-критерій функціонально зв’язаний з
коефіцієнтом детермінації R2, то перевірку
істотності зв’язку можна здійснити,
використовуючи безпосередньо критичні
значення
,
де α — рівень істотності, k1 = m – 1,
k2 = n – (m – 1) — числа
ступенів вільності чисельника та
знаменника, наведено в додатку 10. Оскільки
F-критерій функціонально зв’язаний з
коефіцієнтом детермінації R2, то перевірку
істотності зв’язку можна здійснити,
використовуючи безпосередньо критичні
значення .Критичні
значення коефіцієнта
детермінації R2для
α =0,05
.Критичні
значення коефіцієнта
детермінації R2для
α =0,05
|
|
1 |
2 |
3 |
4 |
5 |
|
8 |
399 |
527 |
604 |
657 |
697 |
|
9 |
362 |
488 |
563 |
618 |
659 |
|
10 |
332 |
451 |
527 |
582 |
624 |
|
12 |
283 |
394 |
466 |
521 |
564 |
|
14 |
247 |
348 |
417 |
471 |
514 |
|
16 |
219 |
312 |
378 |
429 |
477 |
|
18 |
197 |
283 |
345 |
394 |
435 |
|
20 |
179 |
259 |
318 |
364 |
404 |
|
24 |
151 |
221 |
273 |
316 |
353 |
|
28 |
130 |
193 |
240 |
279 |
314 |
|
32 |
115 |
171 |
214 |
250 |
282 |
|
36 |
102 |
153 |
192 |
226 |
256 |
|
40 |
093 |
139 |
176 |
207 |
234 |
|
50 |
075 |
113 |
143 |
170 |
194 |
|
60 |
063 |
095 |
121 |
144 |
165 |
|
80 |
047 |
072 |
093 |
ПО |
127 |
|
100 |
038 |
058 |
075 |
090 |
103 |
|
120 |
032 |
049 |
063 |
075 |
087 |
|
200 |
019 |
030 |
038 |
046 |
053 |
Стандартна таблиця регресійного аналізу містить усі характеристики кореляційних зв'язків, описані вище, зокрема:
• значення коефіцієнтів кореляції R, детермінації R2 та Rk2 (скоригований на число ступенів свободи), стандартну похибку sе;
результати дисперсійного аналізу;
коефіцієнти регресії, стандартні похибки і t-тести коефіієнтів регресії.
Окрім названих множинних коефіцієнтів щільності зв’язку, в комп’ютерних програмах передбачено розрахунок R2 з урахуванням числа ступенів вільності:
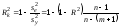 ,
,
де
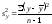 — оцінка дисперсії результативної
ознакиу;
— оцінка дисперсії результативної
ознакиу;
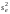 —оцінка
залишкової дисперсії.
—оцінка
залишкової дисперсії.
Скоригований
коефіцієнт множинної детермінації
 відрізняється відR2
співвідношенням числа ступенів вільності
дисперсій: залишкової (n – m + 1)
і загальної (n – 1).
відрізняється відR2
співвідношенням числа ступенів вільності
дисперсій: залишкової (n – m + 1)
і загальної (n – 1).
Лінійна
функція описує такий зв'язок, коли зі
зміною фактора
х
результат
у
змінюється
більш-менш рівномірно. При нерівномірному
співвідношенні варіацій взаємозв'язаних
ознак (наприклад,
коли прирости значень у
зі
зміною х
прискорені чи сповільнені
або напрям зв'язку змінюється),
використовують нелінійні
регресії, зокрема: степеневу, гіперболу,
параболу тощо. Скажімо,
зв'язок між собівартістю у
та
обсягом продукції х
описується
рівнянням гіперболи
![]() ,
деа
-
пропорційні витрати на одиницю продукції,
b
-
постійні витрати на весь випуск, а
зв'язок між ціною і попитом на певний
товар - степеневою функцією
,
деа
-
пропорційні витрати на одиницю продукції,
b
-
постійні витрати на весь випуск, а
зв'язок між ціною і попитом на певний
товар - степеневою функцією
![]() ,
де параметр γ(коефіцієнт
еластичності) характеризує
відносний ефект впливу фактору х
на
результат у.
Якщо
скажімо γ= -08, то це означає, що зі зміною
фактору х
на 1% результату зменшується у середньому
на 0,8%. Степенева функція
зводиться до лінійного виду логарифмуванням
,
де параметр γ(коефіцієнт
еластичності) характеризує
відносний ефект впливу фактору х
на
результат у.
Якщо
скажімо γ= -08, то це означає, що зі зміною
фактору х
на 1% результату зменшується у середньому
на 0,8%. Степенева функція
зводиться до лінійного виду логарифмуванням
![]() .
.
