Двовибіркові t-тести Стьюдента

Другий тип задач пов'язаний з порівнянням параметрів двох сукупностей.

Приклад. Ведеться вибіркове обстеження продуктивності праці двох груп робітників, які виготовляють один і той же виріб на верстатах, модернізованих за різними проектами. Перша група працює на верстатах, модернізованих за проектом А, друга - за проектом Б(п₁=n₂=8). Погодинний виробіток робітників стано­вить, виробів:

Проект А	10	12	15	11	12	9	14	13
Проект Б	8	10	12	9	10	8	11	12

Вибіркові оцінки середніх і дисперсій за групами:

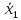= 12 штук при s² = 4,00;

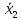= 10 штук при s²= 2,57.

Різниця між середніми (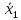-) = (12 - 10) = 2 вироби.

Потрібно визначити, чи істотна розбіжність середніх, тобто чи зумовлена вона різною ефективністю проектів модернізації чи випадкова.

Нульова гіпотеза формулюється на припущенні, що розбіжності середніх ви­падкові Н₀: 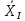=.Альтернативна гіпотеза передбачає, що проект А ефективніший: Н_а: 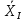>. При такому формулюванні Н_а проводиться одностороння (правостороння) перевірка.

Тестування гіпотези H_о можна виконати за допомогою критерію Стьюдента з числом ступенів свободи df= n₁ + п₂ - 2. Вибі­ркове значення t-тесту обчислюється діленням розбіжності вибіркових середніх на стандартну похибку розбіжності , яка дорівнює сумі стандартних похибок цих середніх

,

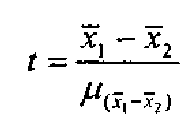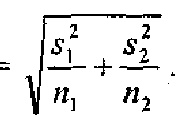
У нашому прикладі стандартна похибка розбіжності середніх дорівнює

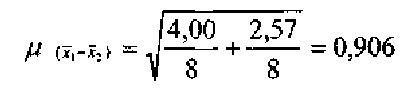
а вибіркове значення t –тесту:

Для числа ступенів свободи df= 8 + 8 - 2 = 14 критичне значення одностороннього критерію t_0,05(14) = 1,76. Оскільки фактичне значення перевищує критичне (2,20 >1,76), нульова гіпотеза відхиляється, і з імовірністю 0,95 можна стверджувати, що розбіжності середніх невипадкові, тобто проект модернізації ве­рстатів А ефективніший за проект Б.

Оцінка розбіжності середніх дещо змінюється, коли ряди спостережень утворюють пари. Така ситуація виникає у повтор­них обстеженнях типу «до - після», скажімо, до і після регулювання пристрою, зміни умов праці, зміни законодавства тощо. У таких випадках два ряди попарно зв'язаних даних замінюються одним рядом відхилень між ними Дисперсія і стандартна похибка цих відхилень визначаються за такими форму­лами

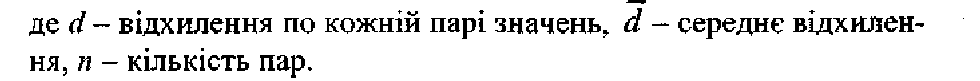
Дисперсійний аналіз

Розглянутий метод двовибіркового тестування розбіжностей середніх перетинається з методом дисперсійного аналізу, в яко­му аналогічна нульова гіпотеза висувається не для двох, а для m - вибірок, кожна з яких представляє ідентифіковану у певний спосіб групу: Н₀:х₁ = х₂ - ...х_т. Тестування такої гіпотези ґрунтується на порівнянні дисперсій, звідси і назва методу Дисперсійний аналіз.

Сутність дисперсійного аналізу полягає в декомпозиції варіації показника за джерелами формування. Кількість джерел варіації залежить від кількості факторів, за якими виокремлено групи. В однофакторному дисперсійному аналізі (скорочено ANOVA) виокремлюються дві компоненти варіації:

• міжгрупова, зумовлена дією фактору, покладеного в основу групування;

• внутрішньогрупова, випадкова варіація.

Основну тотожність однофакторного дисперсійного аналізу можна подати як взаємозв'язок між сумами квадратів відхилень:

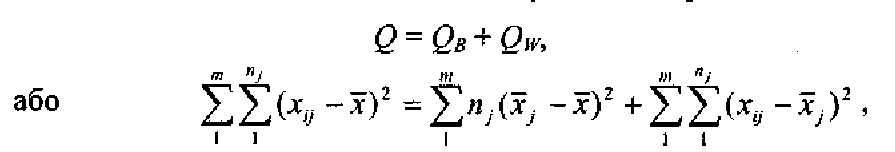
де Q - сума квадратів відхилень окремих спостережень Х_ij від загальної середньої х ;

Q_в - сума квадратів відхилень групових середніх 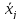від загальної (betwееп);

Q_w - сума квадратів відхилень окремих спостережень Х_ij всередині груп від групових середніх (within);

n_j- - кількість спостережень у j-й групі; т - кількість груп, п = п_jm - загальна кількість спостережень.

На основі сум квадратів відхилень розраховуються три оцінки дисперсій за джерелами варіації:

загальна

міжгрупова

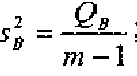
внутрішньогрупова

Знаменники оцінок дисперсії є ступенями свободи відповід­них джерел варіації. Очевидно, вони співвідносяться так само, як суми квадратів відхилень:

Перевірка нульової гіпотези в однофакторному дисперсійному аналізі ґрунтується на співвідношенні міжгрупової і внутрішньогрупової варіації (в розрахунку на одну ступінь свободи). F-тест показує, у скільки разів оцінка міжгрупової варіації перевищує випадкову

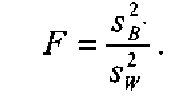
Схема однофакторного дисперсійного аналізу подана в табл. 4.3.1.

Критичні значення. F-тесту для рівня істотності, а визначаються співвідношенням чисел ступенів свободи чисельника (т -1) і знаменника (n - т). Процедура тестування стандартна: коли нульова гіпотеза відхиляється. Якщо , підстав для відхилення нульової гіпотези немає.