2.3 Линеаризация экспоненциальной зависимости

В ряде случаев в качестве эмпирической формулы берут функцию, в которую неопределенные коэффициенты входят нелинейно. При этом иногда задачу удается линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

(2.3)

где инеопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (2.3.1), после чего получаем соотношение:

(2.3)

Обозначим исоответственно черези, тогда зависимость (2.3.1) может быть записана в виде, что позволяет применить формулы (2.2.4) с заменойнаина.

2.4Элементы теории корреляции

График восстановленной функциональной зависимости по результатам измеренийназывается кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности. При этом результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке этой таблицы приводятся численноститех пар, компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой переменной) равными между собой, выбирают центры(соответственно) этих интервалов и числав качестве основы для расчетов.

Коэффициент корреляции является мерой линейной связи между зависимыми случайными величинами: он показывает, насколько хорошо в среднем может быть представлена одна из величин в виде линейной функции от другой.

Коэффициент корреляции вычисляется по формуле:

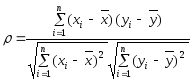, (2.4)

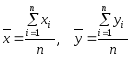где ,и среднее арифметическое значение соответственно по x и y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь междуx и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

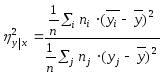, (2.4)

где , а числитель характеризует рассеяние условных среднихоколо безусловного среднего.

Всегда . Равенствосоответствует некоррелированным случайным величинам;тогда и только тогда, когда имеется точная функциональная связь междуy и x. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.

3 Решение задачи с помощью электронных таблиц microsoftexcel

3.1 Расчет коэффициентов аппроксимации

Из графической зависимости y=f(x) рисунка 2.1 определим экспериментальные точки и результаты сведем в таблицу 3.1.

Таблица 3.1 – Экспериментальные точки, полученные из графической зависимости

β=0.7
0.8	0.87
0.9	0.78
1.0	0.75
1.1	0.68
1.2	0.78
1.3	0.99

Расчет коэффициентов аппроксимации согласно условию необходимо произвести для графика зависимости тока статора от напряжения при коэффициенте нагрузки β=0.9.

Для проведения расчетов данные целесообразно расположить в виде таблицы 3.2, используя средства табличного процессора Microsoft Excel.

Таблица 3.2 – Исходные данные для расчета в Microsoft Excel

X	0,80	0,90	1,00	1,10	1,20	1,30
Y	1,10	0,99	0,90	0,88	0,90	1,05

График данной экспериментальной зависимости приведен на рисунке 3.1.

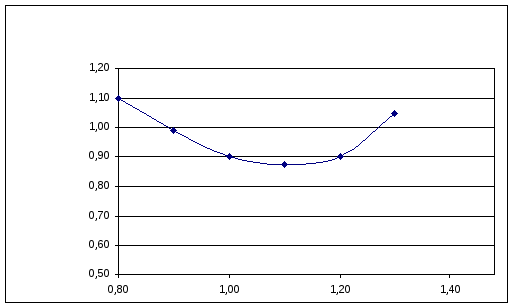
Рисунок 3.1 - График экспериментальной зависимости

Выполним расчет коэффициентов регрессии для линейной зависимости с помощью встроенной статистической функции =ЛИНЕЙН(B3:G3;B2:G2), где в ячейки B3:G3 заносим значения, а в ячейки B2:G2 заносим значения.

Полученные коэффициенты регрессии а и b для линейной зависимости составляют -0,15571 ($A$31) и 1,132667 ($B$31) соответственно.

Теоретические значения , полученные по формуле =$A$31*B3+$B$31 сведены в таблицу 3.3.

Таблица 3.3 – Теоретические значения степенной функции

Yt

0,961381

0,97851

0,992524

0,996417

0,992524

0,969167

Коэффициент корреляции получен по формуле =КОРРЕЛ(B3:G3; B2:G2) и составляет -0,3159, суммарная ошибка получена с помощью формулы =СУММКВРАЗН(B3:G3;B34:G34) и составила 0,057745.

Графическое решение задачи показано на рисунке 3.2. Здесь изображены экспериментальные данные и подобранная к ним линия регрессии.

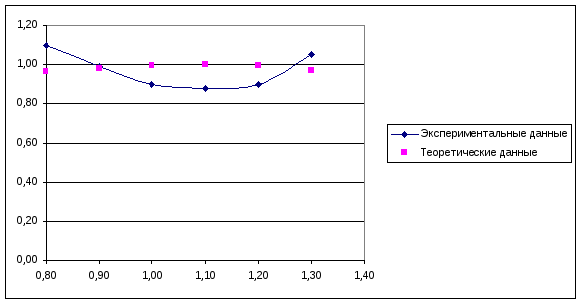Рисунок 3.2 - Графики экспериментальной зависимости и линии регрессии

Расчет коэффициентов регрессии производим для степенной зависимости с помощью встроенной статистической функции =ЛГРФПРИБЛ(B3:G3;B2:G2), где в ячейки B3:G3 заносим значения, а в ячейки B2:G2 заносим значения.

Полученные коэффициенты регрессии а и b для степенной зависимости составляют 0,811933 ($A$7) и 1,194857 ($B$7) соответственно.

Теоретические значения , полученные по формуле =$A$7*СТЕПЕНЬ(B3;$B$7) сведены в таблицу 3.4.

Таблица 3.4 – Теоретические значения степенной функции

Yt

0,929669

0,811933

0,696923

0,67804

0,696923

0,860673

Коэффициент корреляции получен по формуле =КОРРЕЛ(B3:G3; B2:G2) и составляет -0,36245, суммарная ошибка получена с помощью формулы =СУММКВРАЗН(B3:G3;B11:G11) и составила 0,207584.

Расчет параметров полиномиальной функции выполнен аналогично расчету параметров степенной функции, за исключением подбора коэффициентов корреляции а1 ($L$7), а2 ($M$7) и а3 ($N$7) с помощью решающего блока “Поиск решения”.

Полученный результат приведен в таблице 3.5.

Таблица 3.5 – Результат расчета коэффициентов с помощью решающего блока Microsoft Excel

a1	a2	a3
2,421847	-3,93738	2,400122

Теоретические значения , полученные по формуле ==$L$7+$M$7*M2^2+$N$7*M2^3 сведены в таблицу 3.6.

Таблица 3.6 – Теоретические значения полиномиальной функции

Yt

1,130785

0,982256

0,884587

0,852177

0,899427

1,040739

Коэффициент корреляции получен по формуле =(1-L17/КВАДРОТКЛ(M3:R3))^0,5 и составляет 0,991538, суммарная ошибка получена с помощью формулы =СУММКВРАЗН(M3:R3;M11:R11) и составила 0,000977.

Построим в двух графических областях экспериментальные точки и графики подобранных функциональных зависимостей (рисунок 3.3 и рисунок 3.4).

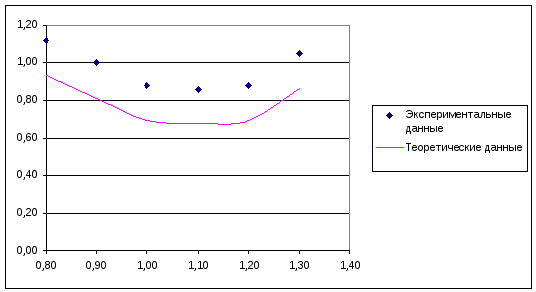Рисунок 3.3 - Графики экспериментальной зависимости и линии регрессии степенной функции

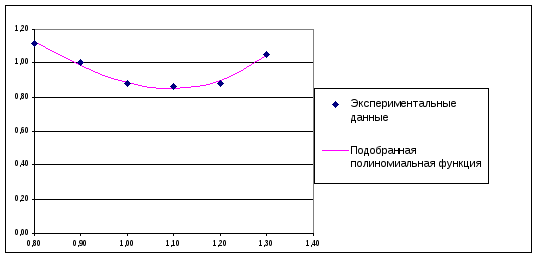Рисунок 3.4 - Графики экспериментальной зависимости и линии регрессии полиномиальной функции

Найдем ожидаемое значение токов при напряжениях 0,87U_1н, 0,96U_1н, 1,22U_1н. Номинальный ток статора 60А.

Используя формулу для степенной функции =$A$7*СТЕПЕНЬ(B44*$B$3;$B$7) и для полиномиальной =$L$7+$M$7*M44*$M$2^2+$N$7*M44*$M$2^3, определим значения функций (таблица 3.7 и таблица 3.8 соответственно).

Таблица 3.7 – Исходные данные и результат расчета степенной функции

U1н	0,87	0,96	1,22
I1н, А	60
It	0,787159	0,885412	1,179006

Таблица 3.8 – Исходные данные и результат расчета полиномиальной функции

U1н	0,87	0,96	1,22
I1н, А	60
It	1,298623	1,182427	0,846751

Ниже приведен результат построения линий тренда по экспериментальным данным в Microsoft Excel (рисунок 3.5). Следует отметить, что при построении степенной линии тренда используется линейная аппроксимация, что вносит погрешность. Таким образом, из построенных зависимостей наиболее точной является полиномиальная линия тренда с четной степенью полинома.

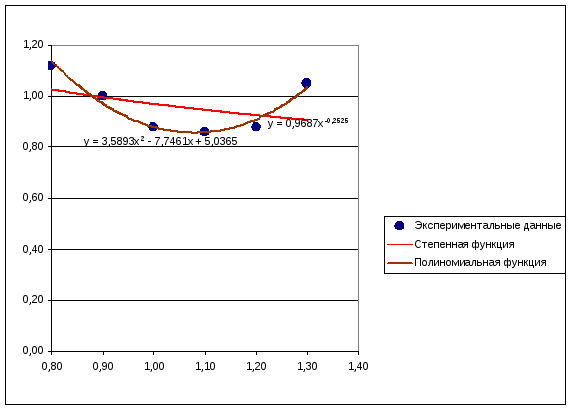
Рисунок 3.5 – Линии тренда