
- •Кафедра прикладной экологии и охраны окружающей среды
- •Характеристика объектов окружающей среды
- •Химический состав, классификация и некоторые особенности природных вод
- •Подразделения вод согласно минерализации
- •Состав поверхностых вод суши
- •Характерные интервалы концентрации биогенных элементов в поверхностных водах суши (в скобках пдк, мг/л)
- •Зависимость содержания nh3 от рН воды при разных температурах
- •Содержание микроэлементов в поверхностных водах суши и биометаллах
- •Молекулярные массы комплексных соединений микроэлементов
- •Характерные интервалы концентраций органических соединений природного происхождения в поверхностных водах суши в мг с/л.
- •Состав подземных вод
- •Состав воздуха и атмосферных осадков
- •Химический состав чистого воздуха
- •Химический состав почв.
- •Группы водосборной площади Днепра
- •Химический состав донных отложений
- •Содержание основных компонентов и микроэлементов в донных отложениях
- •Общая схема анализа и основные этапы
- •Характеристика методов анализа
- •Общая характеристика методов анализа объектов окружающей среды
- •Особенности анализа воздуха
- •Отбор проб
- •Подготовка проб к анализу.
- •Особенности анализа почв и донных отложений.
- •Отбор проб и их подготовка к анализу
- •Основные этапы анализа
- •Особенности анализа природной воды. Виды проб и техника их отбора
- •Отбор проб с водных объектов
- •Консервация, транспортировка и хранение проб воды
- •Определение химических ингредиентов в растворённом состоянии, коллоидно-дисперсной форме и взвесях
- •Концентрирование микрокомпонентов
- •Зависимость количества экстракций n для 99 % извлечения веществ от коэффициента разделения (d) и кратности концентрирования (vвод./vорг.)
- •Удаление веществ, мешающих анализу
- •Автоматизация анализа природных вод
- •Статистическая обработка результатов анализа
- •Зависимость t от n при различных р
Статистическая обработка результатов анализа
Основными характеристиками надёжности результатов химического анализа какого-либо объекта являются их правильность и точность (воспроизводимость)
Правильность анализа – это степень адекватности количества (концентрации) определяемого ингредиента его действительному содержанию в объекте, который анализируется. Критерием правильности анализа является степень совпадения результатов определения определённого ингредиента различными независимыми методами. Например, концентрацию ионов меди в пробе природной воды можно определить методами спектрофотомерии, атомной абсорбции и полярографии. Если средний результат отдельных определений является статистически достоверным, тогда анализ считается правильным.
Такой способ проверки правильности анализа является довольно длительным и громоздким и при анализе природных объектов используется лишь тогда, когда результаты анализа одним методом вызывают сомнения.
Независимо от того, каким способом получено n значений параллельных аналитических измерений, их обрабатывают статистически. Для этого в первую очередь определяют среднее арифметическое значение результатов по формуле:
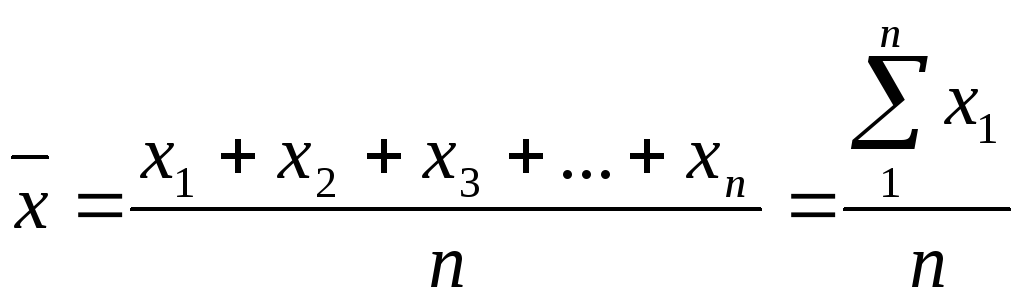 ; (21)
; (21)
Затем вычисляют среднюю квадратичную ошибку (стандартное отклонение) по формуле:
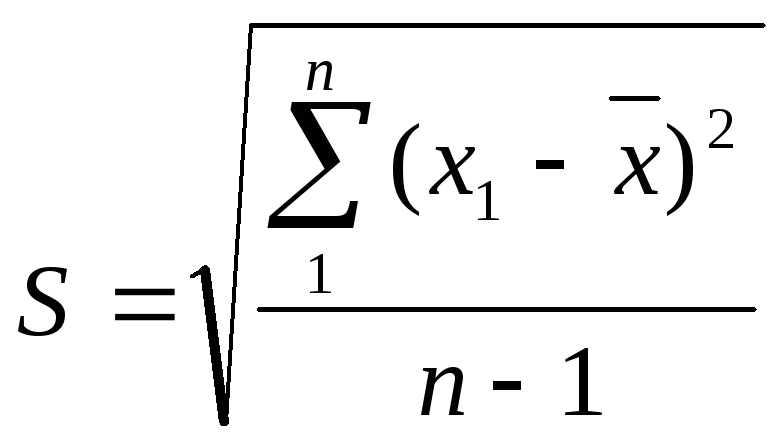 ; (22)
; (22)
и наконец, точность (воспроизводимость) анализа характеризуют величиной доверительного интервала среднего значения, который определяют по формуле:
![]() (23)
(23)
где t(p) – так называемое t распределение. Его величины для разных значений h при вероятностях Р приведены в таблице 14.
Таблица 14.
Зависимость t от n при различных р
-
n
P = 0,90
P = 0,95
P = 0,99
2
6,31
12,7
63,7
3
2,92
4,3
9,92
4
2,35
3,18
5,84
5
2,13
2,78
4,60
6
2,01
2,57
4,03
7
1,94
2,45
3,71
8
1,89
2,36
3,50
10
1,83
2,26
3,25
Результаты анализа
в любых единицах выражаются следующим
образом:
![]()
Значение
![]() конечно вычисляют с вероятностью Р =
0,95 (95 % - ная вероятность)
конечно вычисляют с вероятностью Р =
0,95 (95 % - ная вероятность)
При определении конкретного ингредиента выполняют не более 3 – 4 параллельных анализов, потому что увеличение n незначительно влияет на величину t(p), т.е. на точность анализа.
Из формулы (22)
вытекает, что результат единичного
измерения является статистически
недостоверным, потому что при n
= 1 стандартное отклонение S
и доверительный интервал среднего
значения
![]() принимают бесконечно большую величину.
принимают бесконечно большую величину.
Важным является
определить статистическую достоверность
среднего значения
![]() ,
т.е. убедиться в том, что при выполнении
параллельных анализов не было допущено
случайной грубой ошибки. При небольших
значенияхn
случайные грубые ошибки находят при
помощи разбега варьирования. Для этого
рассчитывают соотношение
,
т.е. убедиться в том, что при выполнении
параллельных анализов не было допущено
случайной грубой ошибки. При небольших
значенияхn
случайные грубые ошибки находят при
помощи разбега варьирования. Для этого
рассчитывают соотношение
![]() (24)
(24)
где х1 – значение, которое вызывает сомнение,х2 – соседнее значение, R – размах варьирования.
Рассчитанную величину Q сравнивают со значением Q (P,n) в таблице15.
-
n
P = 0,90
P = 0,95
P = 0,99
3
0,89
0,94
0,99
4
0,68
0,77
0,89
5
0,56
0,64
0,76
6
0,48
0,56
0,70
7
0,43
0,51
0,64
8
0,40
0,48
0,58
Если Q
> Q(P,
n),
то это указывает на наличие грубой
ошибки. В таком случае соответствующий
результат единичного измерения хi
отбрасывают и повторяют расчёт
![]() ,S
и
,S
и
![]() .
.
Пример. При определении процентного содержания СаО в почве были получены следующие результаты: 2,87; 2,89; 2,90; 2,95. Сомнение вызывает результат 2,95. Проведём расчёты:
![]()
R = 2,95 – 2,87 = 0,08
![]()
В этом случае Q < Q (P, n), что указывает на отсутствие грубой ошибки, т.е. на статистическую достоверность среднего результата.
Это даёт возможность рассчитать содержание СаО по формулам (18) – (20):
![]()
![]()
СаО = 2,90 ± 0,05 %
Пример. При определении концентрации ионов аммония в пробе природной воды получены следующие результаты: 7,10; 7,36; 7,40 и 7,42 мг/л
Сомнение вызывает результат 7,10. Проведём расчёты аналогично предыдущим.
![]() = 7,32; R
= 7,42 – 7,10 = 0,32;
= 7,32; R
= 7,42 – 7,10 = 0,32;
![]()
Т.е. результат 7,10 мг/л является грубой ошибкой и его необходимо выключить из дальнейших расчётов. В таком случае
![]()
![]()
![]() ;
;
CNH+4 = 7,39 ± 0,08 мг/л
Если после исключения грубых ошибок для расчетов остается меньше 3 результатов, то необходимо провести дополнительные анализы.
Особое внимание следует обратить на то, что статистическая обработка результатов анализа, выполненного одним методом, дает возможность обнаружить только случайную ошибку. Если же аналитиком была допущена систематическая ошибка, например, при приготовлении рабочих растворов, при калибровке измерительной аппаратуры и т.д., то обнаружить такую ошибку методом математической статистики невозможно.
Анализ одной пробы, особенно воды или воздуха не может характеризовать с достаточной надежностью ее химический состав, который значительно изменяется во времени и пространстве.
Таким образом,
возникает необходимость анализа серии
проб, которые отобраны через различные
промежутки времени во многих местах
исследуемого природного объекта. На
основании серийных анализов оценивают
средний химический состав исследуемого
природного объекта в целом за конкретный
промежуток времени. Очевидно, что разбег
между результатами серийного анализа
многих проб будет всегда значительно
большим, чем между результатами
параллельных анализов одноразово
отобранной пробы. Поэтому при характеристике
среднего химического состава воды
водохранилищ, речек, озер, воздух большого
города, почву с/х угодий и т.д. статистически
обрабатывают средние результаты
одноразовых анализов. При этом рассчитывают
не только средний результат
![]() ,
а также и статически достоверные
экстремальные значения содержания
конкретного ингардиента хmax
и xmin.
,
а также и статически достоверные
экстремальные значения содержания
конкретного ингардиента хmax
и xmin.
Для таких расчетов
можно применить способ, приемлемый в
случае значений 10<n<1000,
т.е. для статистической обработки
значительного количества результатов
анализа. Суть этого способа заключается
в том, что отбрасывают крайние значения
хі
и рассчитывают
![]() иS.
Статистически недостоверными считают
результаты, которые отклоняются от
иS.
Статистически недостоверными считают
результаты, которые отклоняются от![]() на величину, большую чем 4S.
После исключения недостоверных
результатов рассчитывают
на величину, большую чем 4S.
После исключения недостоверных
результатов рассчитывают
![]() ,
а значения хmax
и xmin
принимают
за достоверные экстремальные величины,
характерные для данного природного
объекта. Графически эти условия можно
изобразить следующим образом:
,
а значения хmax
и xmin
принимают
за достоверные экстремальные величины,
характерные для данного природного
объекта. Графически эти условия можно
изобразить следующим образом:

Пример. В воде озера на протяжении одной недели определяли концентрацию ионов Са и по результатам анализа каждой отобранной пробы получили средние значения: 12,0; 10,1; 8,9; 8,3; 8,0; 7,9; 7,8; 7,6 и 6,5 мг/л. Расчеты по формулам (18) – (20) без учета крайних значений дают следующие результаты:
![]() = 8,4; S
= 0,81;
= 8,4; S
= 0,81;
![]() = 0,68
= 0,68![]() 0,7
0,7
Поскольку xmin
= 6,5 >![]() - 4S
= 5,2 и
хmax
=12,0>
- 4S
= 5,2 и
хmax
=12,0>
![]() + 4S
= 11,6, то результат
+ 4S
= 11,6, то результат
xmin является статистически достоверным, а хmax - недостоверным. Статистически достоверным является соседнее значение хmax = 10,1.
Таким образом, средняя концентрация Са2+ и ее экстремальные значения за исследуемый период были такими:
ССа2+ = 8,4 ±0,7 мг/л ССа2+min = 6,5 мг/л ССа2+max = 10,1 мг/л
Подобные результаты часто записывают в виде дроби, указывая в числителе среднюю концентрацию, а в знаменателе – статистически достоверные экстремальные концентрации:
Са2+
=
![]() мг/л.
мг/л.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРА ТУРЫ
Набиванець Б.М., Сухан В.В., Карабіна Л.В., Аналітична хімія природного середовища. – Київ: Либідь, 1996. – 302 с.
Дмитриев М.Т., Казнина Н.И., Пеничина М.В. Санитарно-химический анализ загрязняющих веществ в окружающей среде. – М.: Химия, 1989. – 368с.
Справочник по физико-химическим методам исследования объектов среды под ред. Арановича Г.И. – Л.: Судостроение, 1979. – 647 с.
Унифицированные методы анализа воды / под ред. Лурье Ю.Ю. – М.: Химия, 1971. – 375 с.
Потіш А.Ф., Медвідь В.Г., Гвоздецький О.Г., Козак З.Я., Екологія: основи теорії і практикум. Навчальний посібник для студентів вищих навчальних закладів. – Львів: Новий світ – 2000 «Магнолія плюс», 2003. – 296 с.
Перегуд Е.Л., Гернет Е.В. Химический анализ воздуха промышленных предприятий. – Л.: Химия, 1973. – 440 с.
Никаноров А.М. Гидрохимия. – Л.: Гидрометеоиздат, 1989. – 351 с.
