
- •Державний вищий навчальний заклад
- •Методичні рекомендації
- •Статистика
- •Донецьк, 2013
- •Тема 1. Методологічні засади статистики
- •Теоретичні основи і зв'язок з іншими науками. Базою для теоретичного обгрунтування категорій і понять статистики є політична економія і діалектичний матеріалізм.
- •Тема 2. Статистичне спостереження
- •Тема 3. Зведення і угрупування статистичних даних. Статистичні таблиці
- •Тема 4. Узагальнюючі статистичні показники
- •4.1 Абсолютні величини і відносні величини
- •4.2 Середні величини
- •Тема 5. Аналіз рядів розподілу
- •Тема 6. Взаємозв'язки статистичних величин
- •1. Слабкі (помітні) зв'язки;
- •2. Сильні (тісні) зв'язки.
- •Тема 7. Ряди Динаміки
- •Тема 8. Статистичні індекси
- •Тема 9. Вибірковий метод
- •Додаток б
- •Продовження додатку б
- •Продовження додатку б
- •Продовження додатку б
- •Продовження додатку б
- •Продовження додатку б
- •Додаток в. Вихідні дані для виконання завдання 4.9 по темі 4
- •Продовження додатку в
- •Продовження додатку в
- •Продовження додатку в
- •Продовження додатку в
- •Продовження додатку в
- •Додаток г
- •Продовження додатку г
- •Додаток д. Вихідні дані до завдань по темі 6
- •Продовження додатку д
- •Продовження додатку д
- •Додаток е. Вихідні дані до завдань по темі 7
- •Додаток ж. Вихідні дані до завдань по темі 8
- •Продовження додатку ж
- •Продовження додатку ж
- •Продовження додатку ж
- •Додаток з
- •Продовження додатку 3
- •Приклад вибору варіанту для виконання контрольної роботи
Тема 5. Аналіз рядів розподілу
Аналітичний матеріал
На відміну від середніх величин, які характеризують те загальне, що характерне для всіх одиниць статистичної сукупності, варіація ознаки характеризує відмінність індивідуальних значень ознаки усередині цієї сукупності.
Під варіацією в статистиці розуміють такі кількісні зміни величини досліджуваної ознаки в межах однорідної сукупності, які обумовлені впливом дії різних чинників, що перехрещується.
Визначення розмаху варіації, середнього лінійного і квадратичного відхилення, коефіцієнтів варіації. Розмах варіації характеризує, на скільки відрізняються крайні значення варіаційної ознаки, розраховується як різниця між найбільшим (хmax ) і найменшим (xmin ) значеннями варіантів:
|
|
(5.1) |
Аби дати узагальнюючу характеристику розподілу відхилень, обчислюють середнє лінійне відхилення d, яке враховує відмінність всіх значень варіаційної ознаки від її середнього значення. Середнє лінійне відхилення, залежно від вигляду варіаційного ряду, розраховується по формулі (5.2) - (5.4):
Дискретний незважений варіаційний ряд:
|
|
(5.2) |
2. Дискретний зважений варіаційний ряд:
|
|
(5.3) |
3. Інтервальний варіаційний ряд:
|
|
(5.4) |
Середнє квадратичне відхилення - це узагальнююча характеристика абсолютних розмірів варіації ознаки в сукупності. Виражається воно в тих же одиницях виміру, що і ознака (у метрах, тоннах, відсотках, гектарах і так далі).
Середнє квадратичне відхилення є мірою надійності середньою. Чим менше середнє квадратичне відхилення, тим краще середня арифметична відображає собою всю сукупність, що представляється.
Середнє квадратичне відхилення, залежно від вигляду варіаційного ряду, розраховується по формулі (5.5) - (5.7):
1. Дискретний незважений варіаційний ряд:
|
|
(5.5) |
2. Дискретний зважений варіаційний ряд:
|
|
(5.6) |
3. Інтервальний варіаційний ряд:
|
|
(5.7) |
Для характеристики міри коливань ознаки, що вивчається, обчислюються показники варіації у відносних величинах. Вони дозволяють порівнювати характер розсіювання в різних розподілах (різні одиниці спостереження однієї і тієї ж ознаки в двох сукупностях, при різних значеннях середніх, при порівнянні різнойменних сукупностей). Розрахунок показників міри відносного розсіювання здійснюють як відношення абсолютного показника варіації до середньої арифметичної.
1. Коефіцієнт осциляції відображає ту, що відносну коливається крайніх значень ознаки довкола середньої:
|
|
(5.8) |
2. Відносне лінійне відхилення характеризує долю усередненого значення абсолютних відхилень від середньої величини:
|
|
(5.9) |
3. Коефіцієнт варіації:
|
|
(5.10) |
Враховуючи, що среднеквадратическое відхилення дає узагальнювальну характеристику тієї, що коливається всіх варіантів сукупності, коефіцієнт варіації є найбільш поширеним показником тієї, що коливається, використовуваним для оцінки типовості середніх величин. При цьому виходять з того, що якщо V більше 40%, то це говорить про ту, що великій коливається ознаки в сукупності, що вивчається.
Розрахунок дисперсії. Дисперсія - це середня арифметична квадратів відхилень кожного значення ознаки від загальної середньої. Дисперсія зазвичай називається середнім квадратом відхилень і позначається . Залежно від вихідних даних дисперсія може обчислюватися по середній арифметичній простій або зваженою:
1. Дискретний незважений варіаційний ряд:
|
|
(5.11) |
2. Дискретний зважений варіаційний ряд:
|
|
(5.12) |
3. Інтервальний варіаційний ряд:
|
|
(5.13) |
Техніка обчислення дисперсії складна, а при великих значеннях варіант і частот може бути громіздкою. Розрахунки можна спростити, використовуючи властивості дисперсії.
Властивості дисперсії.
Зменшення або збільшення частот ознаки в певне число разів дисперсії не змінює.
Зменшення або збільшення кожного значення ознаки на одну і ту ж постійну величину А дисперсії не змінює.
Зменшення або збільшення кожного значення ознаки в k- раз відповідно зменшує або збільшує дисперсію в k2- раз.
Таким чином, при великих значеннях варіаційної ознаки і частот в інтервальних рядах можна спростити, використовуючи спосіб моментів:
|
|
(5.14) |
де h – величина інтервалу;
|
|
(5.15) |
де А – постійна величина, в якості якої зручно вибрати середину інтервалу з найбільшою частотою;
|
|
(5.16) |
|
|
(5.17) |
Розрахунок групової, міжгрупової і загальної дисперсії. Загальна дисперсіявідображає варіацію ознаки за рахунок умов і причин, що діють у всій статистичній сукупності:
|
|
(5.18) |
де
![]() - загальна дисперсія;
- загальна дисперсія;
хі – значення варіаційної ознаки;
![]() – середнє значення варіаційної ознаки;
– середнє значення варіаційної ознаки;
![]() – загальною об'єм статистичної вибірки.
– загальною об'єм статистичної вибірки.
|
|
(5.19) |
де – число однакових значень ознаки xi (вага або частота).
Групова (часткова) дисперсіявідображає варіацію ознаки за рахунок умов і причин, що діють усередині групи:
|
|
(5.20) |
де
![]() - групова дисперсіяj-той
групи (інтервалу) варіаційної ознаки;
- групова дисперсіяj-той
групи (інтервалу) варіаційної ознаки;
![]() –значення i-го
варіаційної ознаки в
j-той групі;
–значення i-го
варіаційної ознаки в
j-той групі;
![]() –середнє значення варіаційної
ознаки в j-той
групі;
–середнє значення варіаційної
ознаки в j-той
групі;
![]() –вага (частота) j-той
групи варіаційної ознаки.
–вага (частота) j-той
групи варіаційної ознаки.
Середня з групових дисперсій– середня арифметична зважена з групових дисперсій:
|
|
(5.21) |
де
![]() – середня з групових дисперсій;
– середня з групових дисперсій;
![]() –
об'єм j-той групи варіаційної ознаки.
–
об'єм j-той групи варіаційної ознаки.
Міжгрупова дисперсіяхарактеризує варіацію результативної ознаки за рахунок ознаки, що є основою групування:
|
|
(5.22) |
де – міжгрупова дисперсія.
Правило складання дисперсій:
|
|
(5.23) |
Визначення показників, що характеризують форму розподілу.Для характеристики форми розподілу ознаки у варіаційному ряду в статистиці використовується система моментів розподілу Чебишева.
Найбільш загальне математичне вираження моменту розподілу записується у вигляді формул (24-26):
1. Дискретний незважений ряд:
|
|
(5.24) |
2. Дискретний зважений ряд:
|
|
(5.25) |
3. Інтервальний ряд
|
|
(5.26) |
де тk - момент k-го порядку;
А, k – постійні числа.
Якщо А – середнє значення ознаки, то отримуємо систему центральних моментів розподілу. Отже дисперсія – це центральний момент розподілу 2-го порядку, а центральні моменти 3-го і 4-го порядку використовуються для характеристики асиметрії і ексцесу розподілу.
При цьому виходять з величини цих моментів в нормальному розподілі, щільність розподілу якого задається функцією:
|
|
(5.27) |
При цьому для нормального розподілу всі центральні моменти непарних порядків дорівнюють нулю (відхилення варіантів, рівновіддалених від середньої, мають рівні частоти), тобто розподіл абсолютний симетрично.
Якщо ж розподіл асиметричний, то частоти рівновіддалених від середньої величини варіантів не рівні між собою і сума непарних мір позитивних відхилень не дорівнює сумі тих же мір негативних відхилень. Тому будь-який центральний момент непарного порядку (вище першого) буде більший або менше нуля залежно від напряму асиметрії розподілу: при правосторонній асиметрії непарні моменти більше нуля, а при лівобічній – менше нуля.
Зазвичай для характеристики міри асиметрії використовують центральний момент 3-го порядку (m3), який залежно від характеру вихідних даних розраховується по формулах (5.28) - (5.30):
1. Дискретний незважений ряд:
|
|
(5.28) |
2. Дискретний зважений ряд:
|
|
(5.29) |
3. Інтервальний ряд:
|
|
(5.30) |
Крім того, аби додати показнику безрозмірний характер, зробити його порівнянним для різних сукупностей, його відносять до куба середнього квадратичного відхилення. Отриманий таким чином показник є нормованим моментом третього порядку. Він служить показником асиметрії і називається асиметрією:
|
|
(5.31) |
Оцінка ексцесу (крутість) розподілу заснована на розрахунку центрального моменту 4-го порядку, співвіднесеного з четвертою мірою середнього квадратичного відхилення:
|
|
(5.32) |
Для нормального розподілу Ех = 3, тому коефіцієнт ексцесу, або просто ексцес знаходять по формулі:
|
|
(5.33) |
Критерії згоди. Критерієм згоди називається критерій перевірки гіпотези про передбачуваний закон невідомого розподілу. Інакше кажучи, він призначений для перевірки гіпотези про те, що ряд спостережень утворює випадкову вибірку, що створена з генеральної сукупності Х з функцією розподілу F(X), де загальний вигляд F(X) вважається відомим.
Найчастіше в статистиці використовують критерії згоди Пірсона і Колмогорова .
Теоретичний розподіл – це розподіл вірогідності деякої випадкової величини, вибраний для опису закону, якому підкоряється фактичний розподіл.
Найчастіше на практиці застосовують нормальний розподіл (розподіл Гауса).
Нормальний розподіл – це розподіл вірогідності з щільністю:
|
|
(5.34) |
У статистичній практиці використовується нормований нормальний розподіл, який є нормальним розподілом з нульовим математичним чеканням і одиничною дисперсією.
Перехід до нормованого нормального розподілу здійснюється відповідно до формули:
|
|
(5.35) |
де t – аргумент функції нормального нормованого розподілу;
![]() –
верхній кордон інтервалу в інтервальному
розподілі.
–
верхній кордон інтервалу в інтервальному
розподілі.
Щільність розподілу нормованого нормального розподілу тоді має вигляд:
|
|
(5.35) |
Відповідно, функція розподілу нормованого нормального розподілу має вигляд:
|
|
(5.35) |
Значення функції F(t) наводяться в довідкових таблицях.
Алгоритм вживання критерію Пірсона полягає в наступному:
з генеральної сукупності утворюється випадкова вибірка і на її основі робиться припущення (гіпотеза) про закон розподілу ознаки генеральної сукупності;
обчислюються параметри цього закону;
обчислюються теоретичні частоти
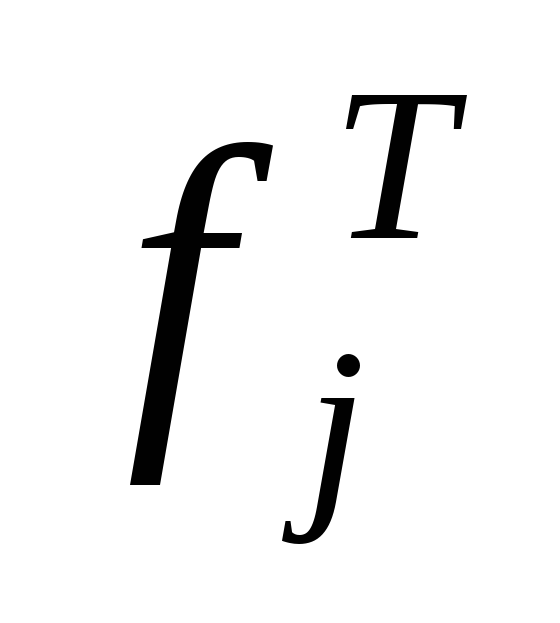 ;
;по формулі
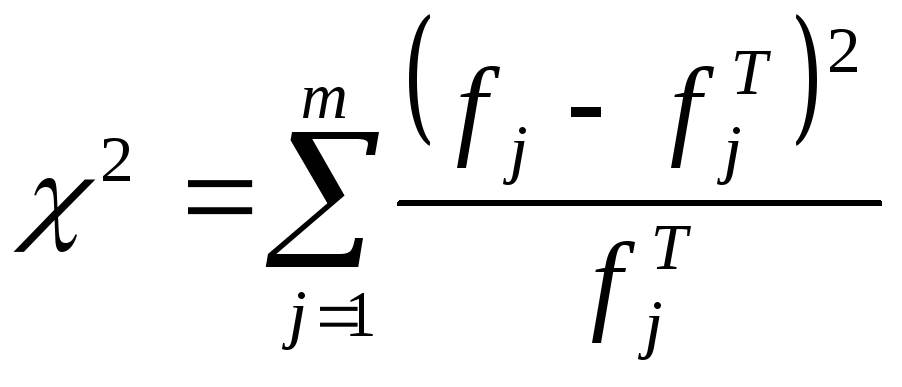 знаходиться
знаходиться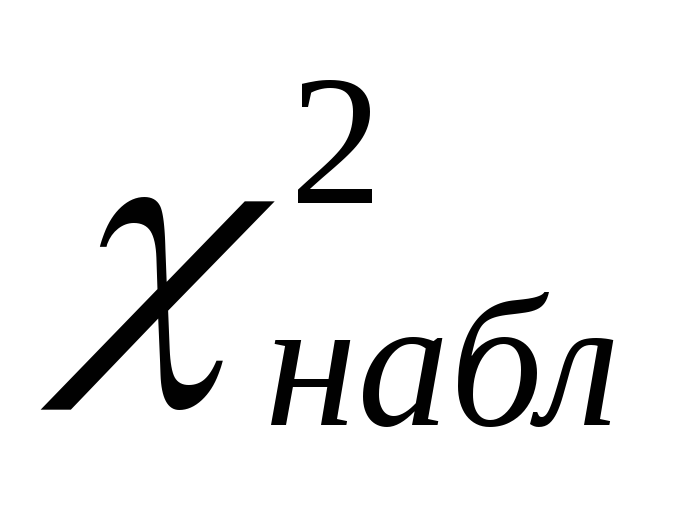 ;
;обчислюється число мір свободи
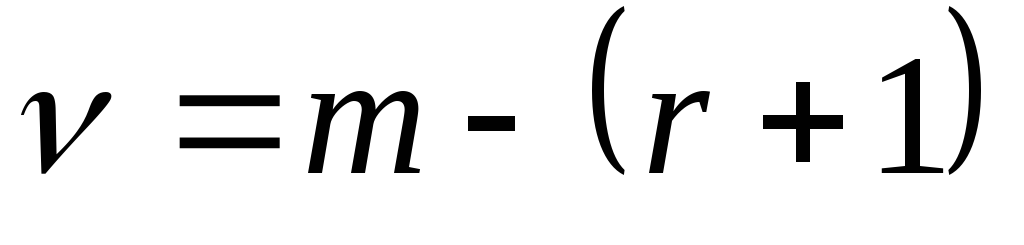 ,
деm –
число інтервалів вибірки; r
– сума числа параметрів
передбачуваного розподілу;
,
деm –
число інтервалів вибірки; r
– сума числа параметрів
передбачуваного розподілу;вибирається рівень значущості
 ;
;з таблиці при мірі свободи
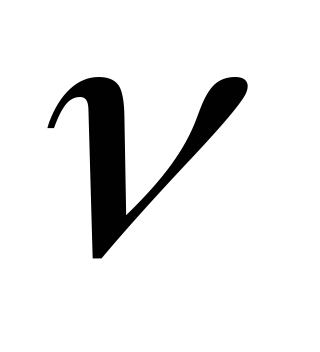 і рівні значущості
і рівні значущості вибирається критичне значення критерію
вибирається критичне значення критерію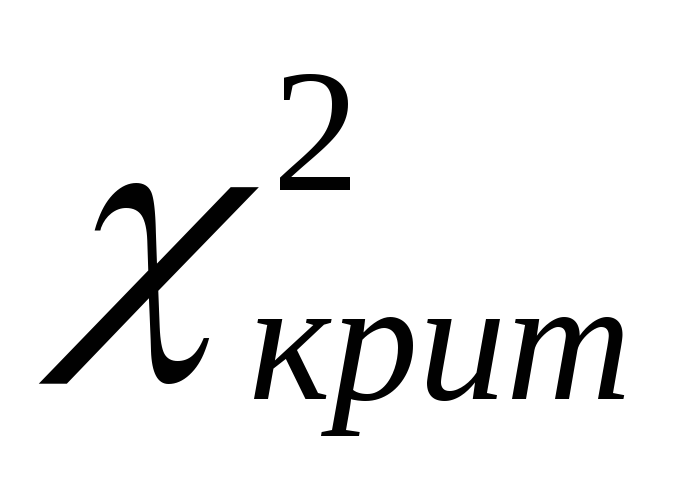 ,
яке порівнюється з
,
яке порівнюється з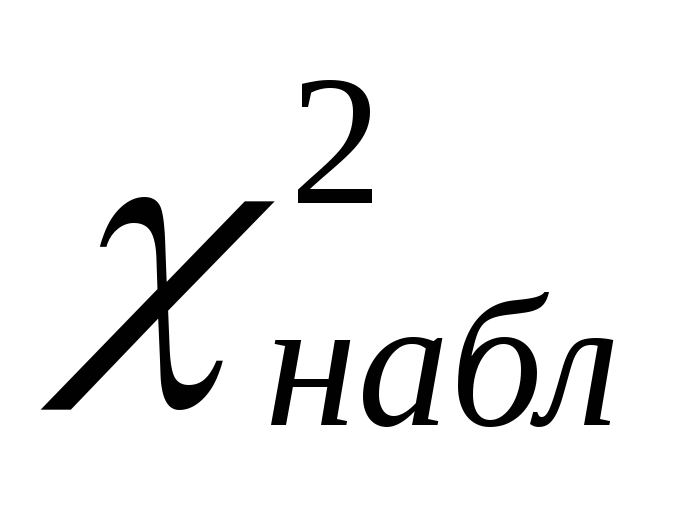 .
Якщо
.
Якщо
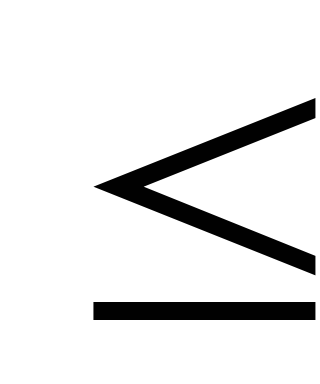
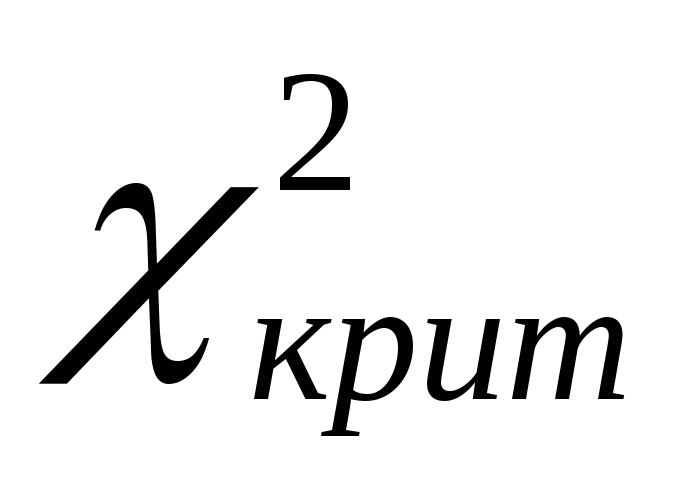 ,
слід вважати неістотним розбіжність
між теоретичними і емпіричними частотами.
В цьому випадку гіпотеза про розподіл
ознаки генеральної сукупності по
передбачуваному закону підтверджується.
Інакше – гіпотеза відкидається.
,
слід вважати неістотним розбіжність
між теоретичними і емпіричними частотами.
В цьому випадку гіпотеза про розподіл
ознаки генеральної сукупності по
передбачуваному закону підтверджується.
Інакше – гіпотеза відкидається.
При вирішенні завдань в загальній теорії статистики зазвичай висувається гіпотеза про нормальний нормований закон розподілу ознаки генеральної сукупності. Отже алгоритм вживання критерію Пірсона модифікується таким чином:
розрахунок середнього значення за варіаційною ознакою;
розрахунок середньоквадратичного відхилення по вибірці;
розрахунок
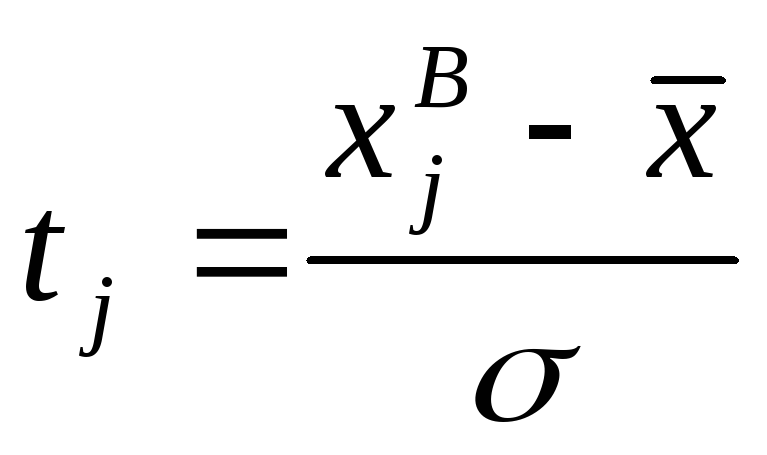 ;
;розрахунок
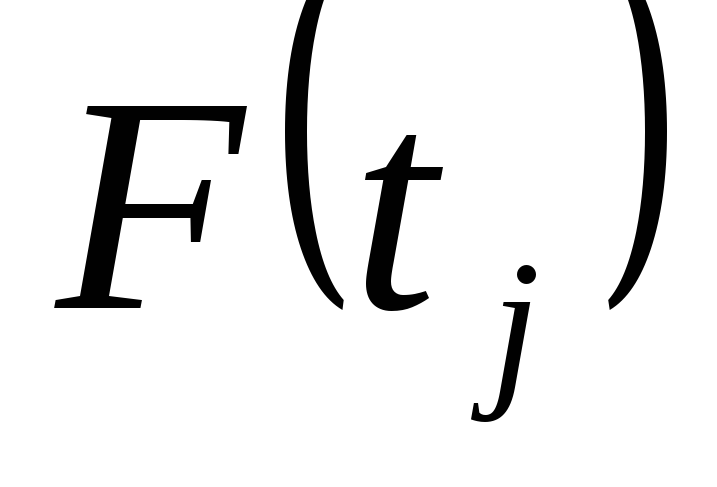 за допомогою довідкової таблиці;
за допомогою довідкової таблиці;розрахунок
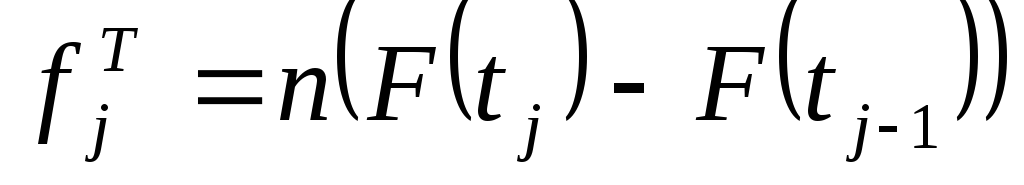 ,
при чому
,
при чому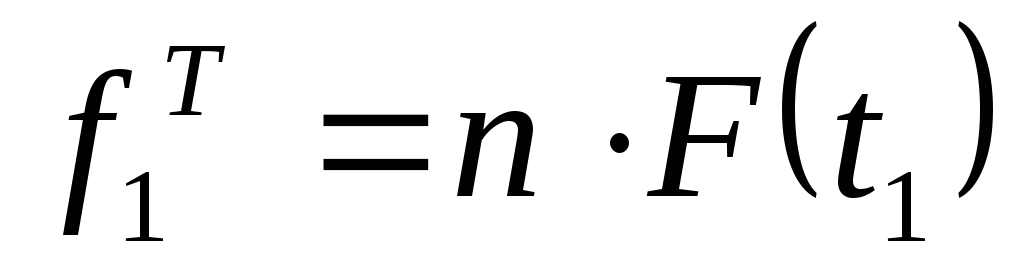 ;
;розрахунок спостережуваного значення критерію Пірсону
 ;
;
обчислюється число мір свободи
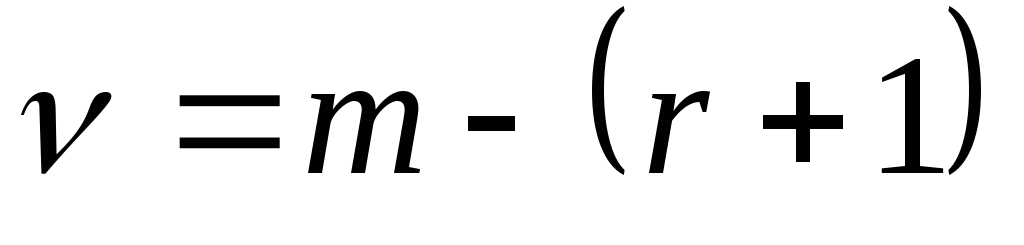 ,
деm –
число інтервалів вибірки; r
– сума числа параметрів передбачуваного
розподілу (для нормального нормованого
розподілу
,
деm –
число інтервалів вибірки; r
– сума числа параметрів передбачуваного
розподілу (для нормального нормованого
розподілу
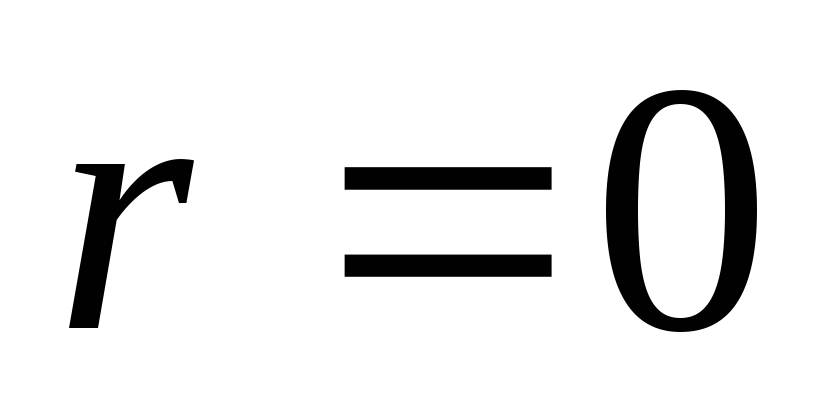 );
);вибирається рівень значущості
 ;
;з таблиці при мірі свободи
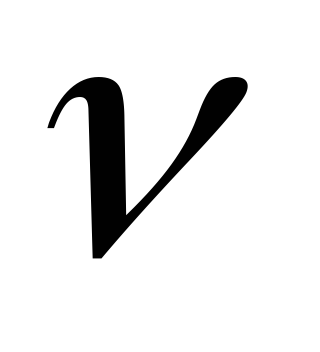 і рівні значущості
і рівні значущості вибирається критичне значення критерію
вибирається критичне значення критерію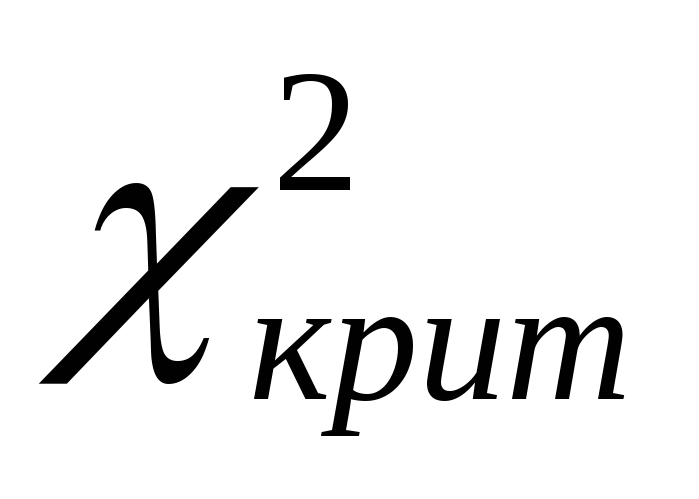 ,
яке порівнюється з
,
яке порівнюється з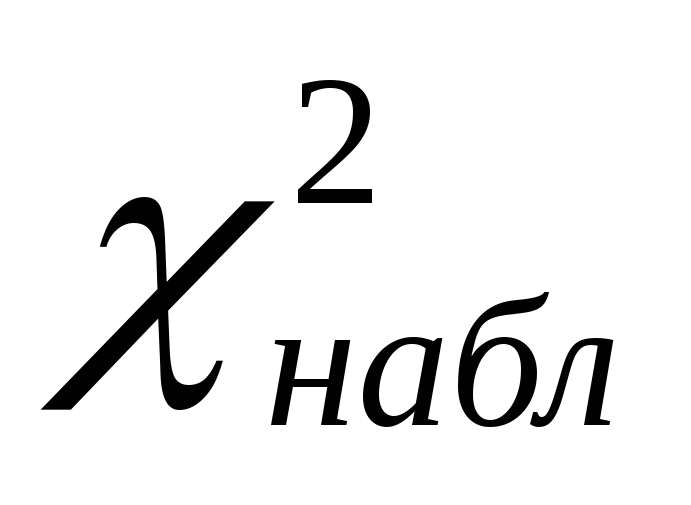 .
Якщо
.
Якщо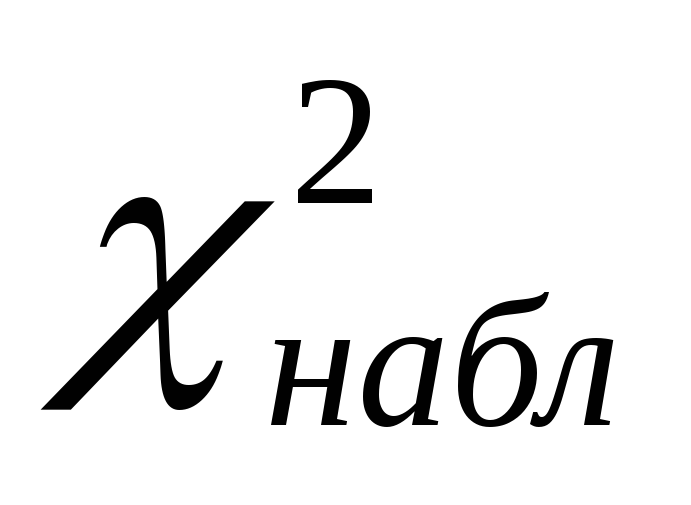

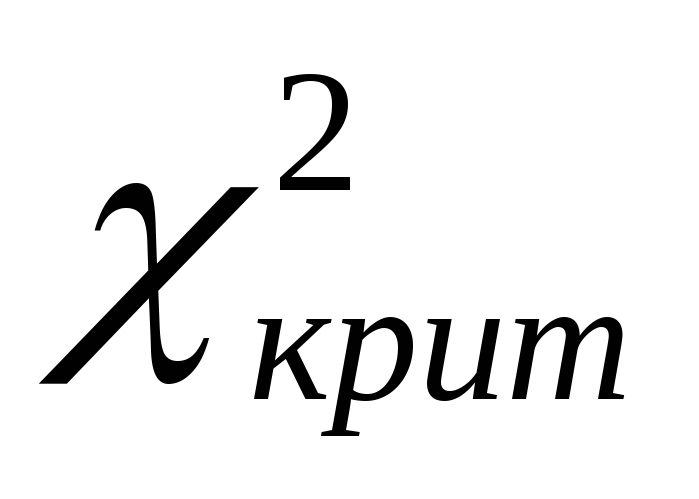 ,
слід вважати неістотним розбіжність
між теоретичними і емпіричними частотами.
В цьому випадку гіпотеза про розподіл
ознаки генеральної сукупності по
передбачуваному закону підтверджується.
Інакше – гіпотеза відкидається.
,
слід вважати неістотним розбіжність
між теоретичними і емпіричними частотами.
В цьому випадку гіпотеза про розподіл
ознаки генеральної сукупності по
передбачуваному закону підтверджується.
Інакше – гіпотеза відкидається.
Якщо закон розподілу ознаки Х з безперервною варіацією відомий (тобто вигляд функції і числові значення параметрів відомі), то можна застосовувати критерій згоди Колмогорова. При його використанні порівнюються емпірична і гіпотетична функції розподілу, а не емпіричні і теоретичні частоти, як в разі критерію Пірсона.
Алгоритм вживання критерію Колмогорова:
результати вибірки з генеральної сукупності представляють у вигляді інтервального ряду або представляють в зростаючому порядку;
знаходять емпіричну функцію розподілу
![]() ,
,
де
![]() –
накопичена частотаj-го
інтервалу.
–
накопичена частотаj-го
інтервалу.
обчислюють значення передбачуваної теоретичної функції розподілу
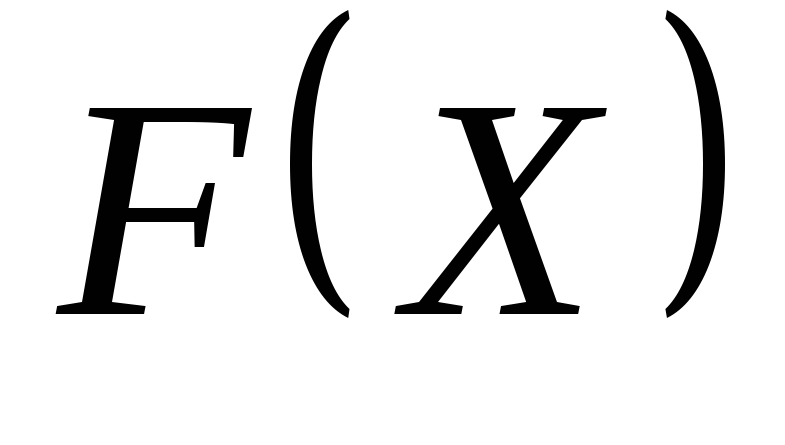 за даними вибірки;
за даними вибірки;для кожного значення
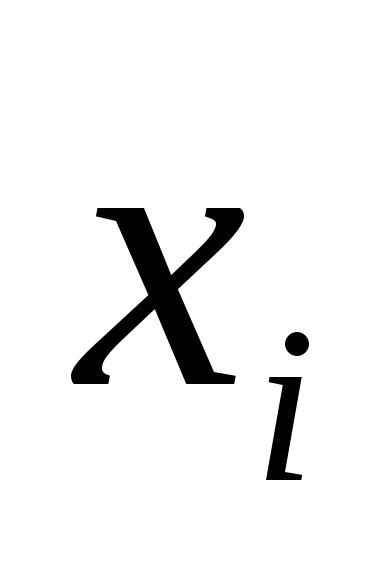 обчислюють
обчислюють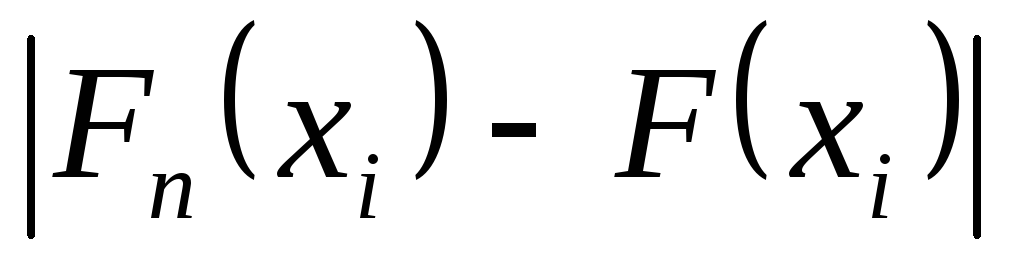 ;
;обчислюють спостережуване значення вибіркової статистики
 Колмогорова
Колмогорова
![]()
по заданому рівню значущості з довідкових таблиць знаходять критичне значення критерію Колмогорова
 ;
;якщо
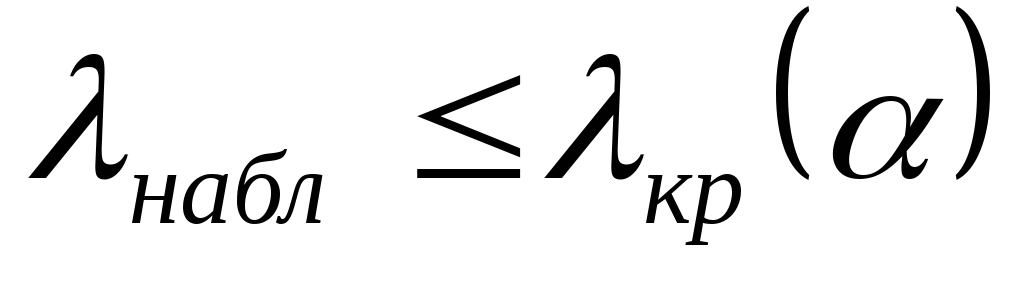 ,
то спостережувані дані добре узгоджуються
з теоретичним розподілом; якщо
,
то спостережувані дані добре узгоджуються
з теоретичним розподілом; якщо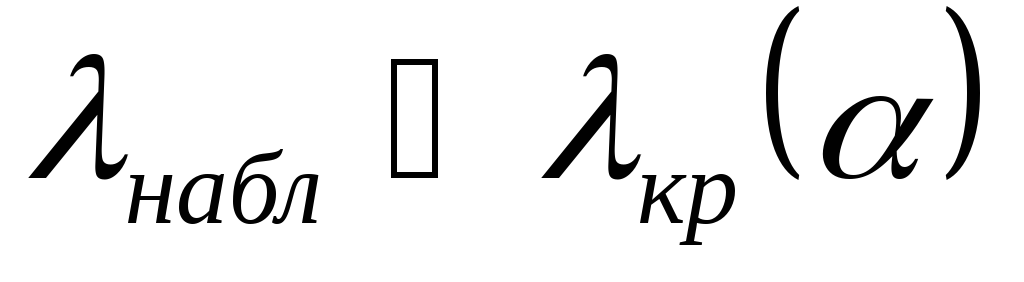 ,
то гіпотеза, що перевіряється,
відхиляється.
,
то гіпотеза, що перевіряється,
відхиляється.
При вирішенні завдань в загальній теорії статистики зазвичай висувається гіпотеза про нормальний нормований закон розподілу ознаки генеральної сукупності. Отже, алгоритм вживання критерію Колмогорова модифікується таким чином:
розрахунок середнього значення за варіаційною ознакою;
розрахунок середньоквадратичного відхилення по вибірці;
розрахунок
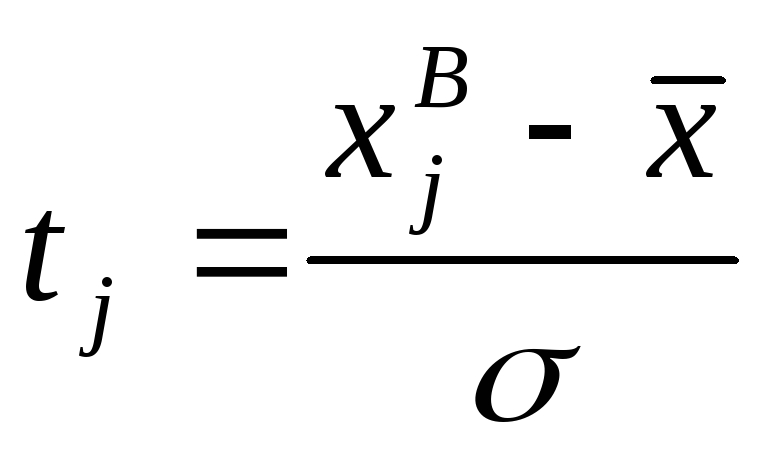 ;
;розрахунок
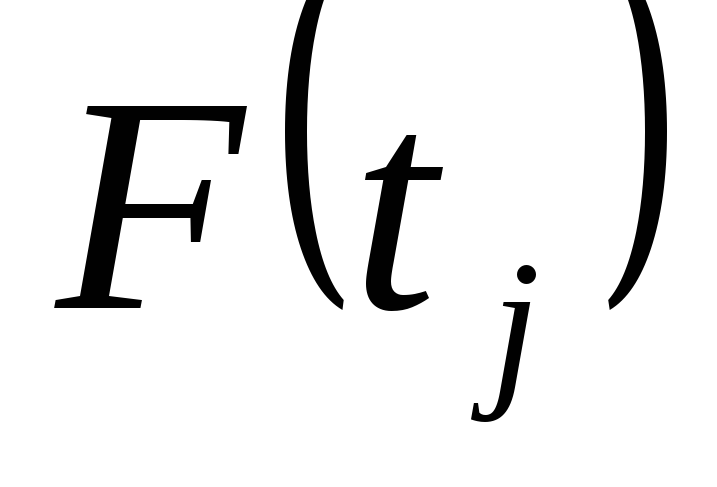 за допомогою довідкової таблиці;
за допомогою довідкової таблиці;розрахунок накопичених частот;
розрахунок емпіричної функції розподілу
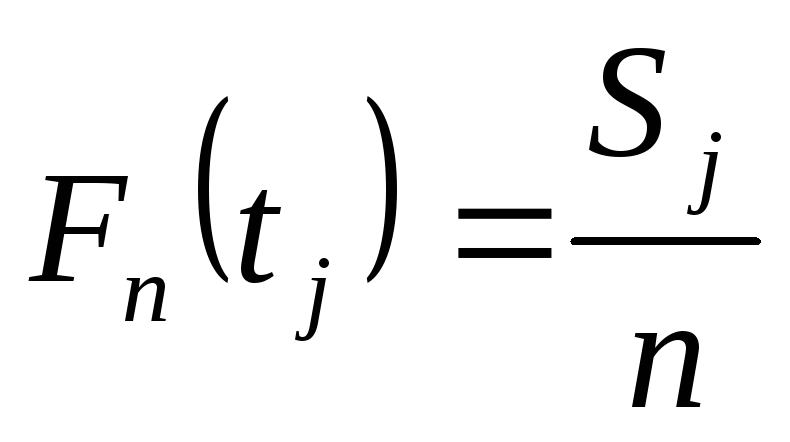 ;
;розрахунок значень
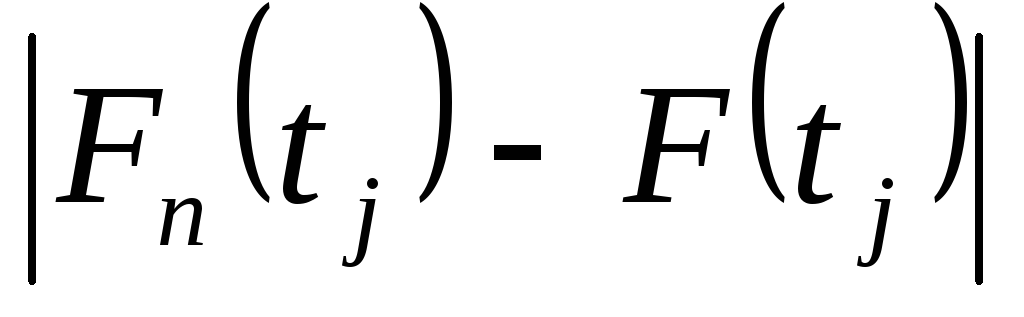 ;
;знаходження
 ;
;обчислюють спостережуване значення вибіркової статистики
 Колмогорова:
Колмогорова:
![]() ;
;
по заданому рівню значущості
 з довідкових таблиць знаходять критичне
значення критерію Колмогорова
з довідкових таблиць знаходять критичне
значення критерію Колмогорова ;
;якщо
 ,
то спостережувані дані добре узгоджуються
з теоретичним розподілом; якщо
,
то спостережувані дані добре узгоджуються
з теоретичним розподілом; якщо ,
то гіпотеза, що перевіряється,
відхиляється.
,
то гіпотеза, що перевіряється,
відхиляється.
Приклади вирішення завдань
Приклад 1. Визначте абсолютні і відносні показники варіації собівартості одиниці продукції, за даними наведеними в таблиці:
|
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
|
До 2,2 |
2 |
3,0-3,4 |
6 |
|
2,2-2,6 |
3 |
3,4- 3,8 |
10 |
|
2,6-3,0 |
5 |
Більше 3,8 |
4 |
Рішення
1) Формули для розрахунку абсолютних показників варіації мають вид:
|
|
|
|
|
|
2) Формули для розрахунку відносних показників варіації мають вигляд:
|
|
|
|
|
|
3)
![]() ;
;![]() .
.
4) Рішення задачі наведемо в таблиці:
|
Групи
по
|
|
|
|
|
( |
( |
|
|
|
1,8 – 2,2 |
2 |
2,0 |
4,0 |
- 1,0 |
1,00 |
2,00 |
1,0 |
2,0 |
|
2,2 – 2,6 |
3 |
2,4 |
7,2 |
- 0,6 |
0,36 |
1,08 |
0,6 |
1,8 |
|
2,6 – 3,0 |
5 |
2,8 |
14,0 |
- 0,2 |
0,04 |
0,20 |
0,2 |
1,0 |
|
3,0 – 3,4 |
6 |
3,2 |
13,2 |
0,2 |
0,04 |
0,24 |
0,2 |
1,2 |
|
3,4 – 3,8 |
10 |
3,6 |
36,0 |
0,6 |
0,36 |
3,60 |
0,6 |
6,0 |
|
3,8 – 4,2 |
4 |
4,0 |
16,0 |
1,0 |
1,00 |
4,00 |
1,0 |
4,0 |
|
Усього |
30 |
|
90,4 |
|
|
11,12 |
|
16,0 |
5)
d=
![]() грн.;
грн.;
![]() 0,61 грн.;
0,61 грн.;![]() 3,0
грн.
3,0
грн.
6) Kd = 0,53/3,0 = 0,18; V = 0,61/3,0 = 0,20.
Відповідь. Середнє лінійне відхилення складає – 0,53 грн.; середнє квадратичне відхилення – 0,61 грн.; відносне лінійне відхилення – 0,18; коефіцієнт варіації – 0,20.
Приклад 2. Визначте дисперсію собівартості одиниці продукції, за даними наведеними в таблиці:
|
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
|
До 2,2 |
2 |
3,0-3,4 |
6 |
|
2,2-2,6 |
3 |
3,4- 3,8 |
10 |
|
2,6-3,0 |
5 |
Більше 3,8 |
4 |
Рішення
1) Формула для розрахунку дисперсії має наступний вигляд:
 ;
;
2)
![]() ;
;![]() .
.
3) Рішення задачі наведено у таблиці:
|
Групи
по
|
|
|
|
|
( |
( |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
1,8 – 2,2 |
2 |
2,0 |
4,0 |
- 1,0 |
1,00 |
2,00 |
|
2,2 – 2,6 |
3 |
2,4 |
7,2 |
- 0,6 |
0,36 |
1,08 |
|
2,6 – 3,0 |
5 |
2,8 |
14,0 |
- 0,2 |
0,04 |
0,20 |
|
3,0 – 3,4 |
6 |
3,2 |
13,2 |
0,2 |
0,04 |
0,24 |
|
3,4 – 3,8 |
10 |
3,6 |
36,0 |
0,6 |
0,36 |
3,60 |
|
3,8 – 4,2 |
4 |
4,0 |
16,0 |
1,0 |
1,00 |
4,00 |
|
Усього |
30 |
|
90,4 |
|
|
11,12 |
4)
![]() грн.;
грн.;
5)
![]() 0,37.
0,37.
Відповідь. Дисперсія собівартості одиниці продукції – 0,37.
Приклад 3. За даними наведеними у таблиці визначте дисперсію обсягу випуску продукції підприємством за способом моментів:
|
Групи підприємств за обсягом виробництва продукції, тис. грн. |
Кількість підприємств |
|
до 4000 |
12 |
|
4000 – 6000 |
20 |
|
6000 – 8000 |
40 |
|
8000 – 10000 |
18 |
|
понад 10000 |
10 |
|
Усього |
100 |
Рішення
1) Формула для розрахунку дисперсії ознаки по способу моментів має наступний вигляд:
![]()
![]() .
.
2)
![]()
![]() ;
;![]() ;
;![]()
![]() .
.
3) Рішення представимо у таблиці:
|
Групи
підприємств по
|
|
|
|
|
|
|
|
|
|
2000 - 4000 |
12 |
3000 |
- 4000 |
- 2 |
6 |
- 12 |
4 |
24 |
|
4000 – 6000 |
20 |
5000 |
- 2000 |
- 1 |
10 |
- 10 |
1 |
10 |
|
6000 – 8000 |
40 |
7000 |
0 |
0 |
20 |
0 |
0 |
0 |
|
8000 – 10000 |
18 |
9000 |
2000 |
1 |
9 |
9 |
1 |
9 |
|
10000 - 12000 |
10 |
11000 |
4000 |
2 |
5 |
10 |
4 |
20 |
|
Усього |
100 |
|
|
|
50 |
-3 |
|
63 |
![]() ,
,
![]() ,
,![]() .
.
![]() =
5025600.
=
5025600.
Відповідь. Дисперсія обсягу випуску продукції підприємством складає 5025600.
Приклад 4. Є наступні дані про розподіл робочих по відсотку браку, що допускається, в процесі виробництва:
|
Групи по відсотку браку, % |
Число робочих |
Середній відсоток браку продукції на одного робітника, % |
Середнє квадратичне відхилення |
|
до 1 |
5 |
0,8 |
0.67 |
|
1 – 3 |
35 |
2,3 |
0.78 |
|
3 – 5 |
17 |
3,9 |
0,51 |
|
понад 5 |
4 |
5,8 |
0.48 |
Визначите загальну дисперсію браку продукції, що допускається робітниками , застосовуючи правило складання дисперсій.
Рішення
1) Загальна дисперсія (формула складання дисперсій):
![]() .
.
2)
![]() ;
;![]()
![]()
![]()
![]()
3) Рішення задачі надамо в табличному вигляді:
|
№ групи |
|
|
|
|
|
( |
( |
|
|
|
1 |
5 |
0,8 |
0,67 |
4,0 |
- 2,0 |
4,00 |
20,00 |
0,45 |
2,25 |
|
2 |
35 |
2,3 |
0,78 |
80,3 |
- 0,5 |
0,25 |
8,75 |
0,61 |
21,35 |
|
3 |
17 |
3,9 |
0,51 |
66,3 |
1,1 |
1,21 |
20,57 |
0,26 |
4,42 |
|
4 |
4 |
5,8 |
0,48 |
23,2 |
3,0 |
9,00 |
36,00 |
0,23 |
0,92 |
|
Усього |
61 |
|
|
173,8 |
|
|
85,32 |
|
28,94 |
4)
![]() %;
%;![]() ;
;![]() 0,474
;
0,474
;
5)
![]() .
.
Відповідь. Загальна дисперсія браку продукції, що допускається робітниками складає – 1,873.
Приклад 5. За даними наведеними в таблиці визначте асиметрію та ексцес розподілу собівартості одиниці продукції:
|
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
|
До 2,2 |
2 |
3,0-3,4 |
6 |
|
2,2-2,6 |
3 |
3,4- 3,8 |
10 |
|
2,6-3,0 |
5 |
Більше 3,8 |
4 |
Рішення
1) Показники асиметрії та ексцесу розраховуються по наступним формулам:
![]() ;
;
![]() ;
;
2) Моменти розподілу визначають наступним чином:
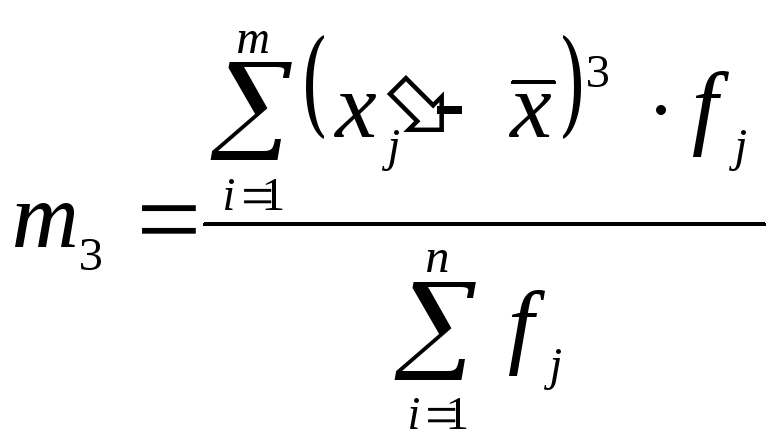 ;
;
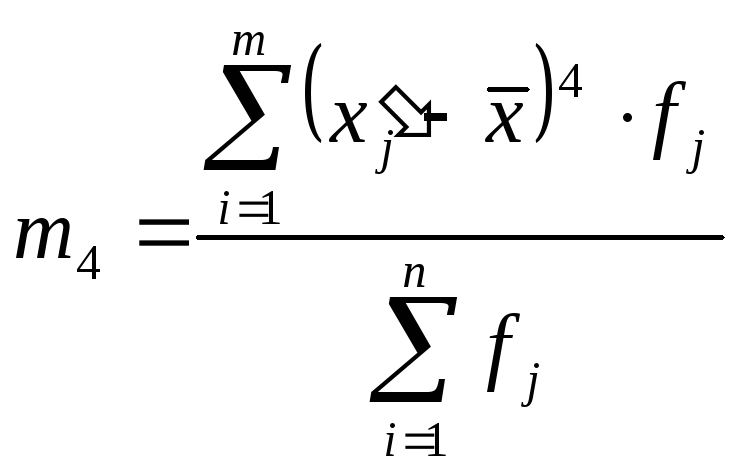 ;
;
3) Для прискорення рішення скористаємося даними стовбців 1, 2, 5 таблиці та значенням дисперсії (прикладу 2), яка вже розрахована для цього інтервального ряду. Результати розрахунків надамо в таблиці:
|
Групи
по
|
|
|
|
|
|
|
|
1 |
2 |
5 |
|
|
|
|
|
1,8 – 2,2 |
2 |
- 1,0 |
- 1,0 |
- 2,0 |
1,0 |
2,0 |
|
2,2 – 2,6 |
3 |
- 0,6 |
- 0,216 |
- 0,648 |
0,1296 |
0,3888 |
|
2,6 – 3,0 |
5 |
- 0,2 |
- 0,008 |
- 0,04 |
0,0016 |
0,008 |
|
3,0 – 3,4 |
6 |
0,2 |
0,008 |
0,048 |
0,0016 |
0,0096 |
|
3,4 – 3,8 |
10 |
0,6 |
0,216 |
2,16 |
0,1296 |
12,96 |
|
3,8 – 4,2 |
4 |
1,0 |
1,0 |
4,0 |
1,0 |
4,0 |
|
Усього |
30 |
|
|
3,52 |
|
19,3664 |
4)
![]() ;
;![]() .
.
5)
![]() 0,53
;
0,53
;![]() 1,74
.
1,74
.
Відповідь. Показник асиметрії дорівнює 0,53, це свідчить про незначну правосторонню асиметрію. Показник ексцесу склав 1,74, що свідчить про гостро вершинний розподіл.
Приклад 6. За даними наведеними в таблиці перевірте гіпотезу про нормальний розподіл варіаційної ознаки за допомогою критерію згоди Пірсона:
|
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
Групи підприємств по собівартості одиниці продукції, грн. |
Число підприємств |
|
До 2,2 |
2 |
3,0-3,4 |
6 |
|
2,2-2,6 |
3 |
3,4- 3,8 |
10 |
|
2,6-3,0 |
5 |
Більше 3,8 |
4 |
Рішення
1) Для прискорення рішення скористаємося даними стовбців 1, 2 таблиці та значенням дисперсії та середньої арифметичної (приклад 2), які вже розраховані для цього інтервального ряду.
Нормоване (стандартизоване) значення ознаки розрахуємо по формулі:
![]() ;
;
![]() =
=![]() 0,61;
0,61;![]() 3
грн.
3
грн.
2) Теоретичні частоти розраховуються за формулою:
![]() ;
;
![]() ;
;
3) Критерій Пірсона визначається наступнім чином:
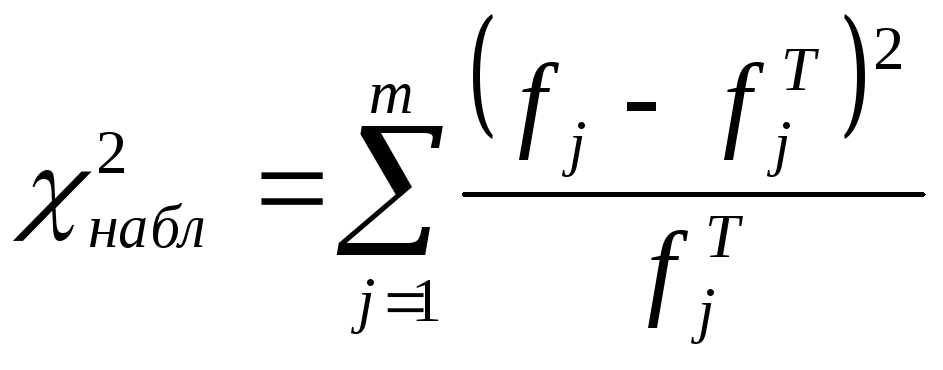 ;
;
4) Розрахунки виконаємо в таблиці. Для прискорення рішення скористаємося даними стовбців 1, 2 таблиці та значенням дисперсії (прикладу 2), яка вже розрахована для цього інтервального ряду.
|
Групи
по
|
|
tj |
|
f jT |
|
|
|
|
1,8 – 2,2 |
2 |
- 1,31 |
0,095 |
2,85 |
- 0,85 |
0,7225 |
0,2535 |
|
2,2 – 2,6 |
3 |
- 0,66 |
0,255 |
4,80 |
- 2,80 |
7,8400 |
1,6333 |
|
2,6 – 3,0 |
5 |
0,00 |
0,500 |
7,35 |
- 2,35 |
5,5225 |
0,7514 |
|
3,0 – 3,4 |
6 |
0,66 |
0,745 |
7,35 |
- 1,35 |
1,8225 |
0,2480 |
|
3,4 – 3,8 |
10 |
1,31 |
0,905 |
4,80 |
5,2 |
27,0400 |
5,6333 |
|
3,8 – 4,2 |
4 |
1,97 |
0,975 |
2,1 |
1,9 |
3,6100 |
1,7190 |
|
Усього |
30 |
|
|
29,25 |
|
|
10,2385 |
5)
![]() ;
;![]() =
6 – (0+1) = 5;
=
6 – (0+1) = 5;
6) При
![]() =
10 % та
=
10 % та![]() = 5
= 5![]()
![]() 9,2.
9,2.
Відповідь. Оскільки
![]() >
>![]() 9,2,
то гіпотеза про нормальний розподіл
варіаційної ознаки не підтверджується.
9,2,
то гіпотеза про нормальний розподіл
варіаційної ознаки не підтверджується.
Тести
1. Для порівняння варіації двох різних ознак можна використовувати наступні показники варіації:
а) розмах варіації;
б) середнє лінійне відхилення;
в) середнє квадратичне відхилення;
г) коефіцієнти варіації.
2. Що станеться з дисперсією, якщо кожен признак збільшити або зменшити на одну і ту ж постійну величину ( А )? Дисперсія при цьому:
а) не зміниться;
б) відповідно збільшиться або зменшиться на величину А;
в) відповідно зменшиться або збільшиться на величину А;
г) зміну дисперсії неможливо передбачити.
3. Що станеться з дисперсією, якщо кожен признак збільшити або зменшити в одне и те ж число раз ( А )? Дисперсія при цьому:
а) не зміниться;
б) відповідно збільшиться або зменшиться на величину А;
в) відповідно збільшиться або зменшиться на величину А2;
г) зміну дисперсії неможливо передбачити.
4. Що станеться з дисперсією, якщо кожен важіль (частоту) збільшити або зменшити в одне и те ж число раз ( А )? Дисперсія при цьому:
а) не зміниться;
б) відповідно збільшиться або зменшиться на величину А;
в) відповідно збільшиться або зменшиться на величину А2;
г) зміну дисперсії неможливо передбачити.
5. Графічне представлення розподілу ознаки у дискретному варіаційному ряду можна зробити за допомогою:
а) гістограми частот;
б) полігону частот;
в) і гістограми і полігону частот;
г) не можливо представити графічно.
6. Значення коефіцієнта асиметрії складає (Кa = - 0.35 ). Це свідчить про те, що розподіл:
а) симетричний;
б) має місце правостороння асиметрія;
в) має місце лівостороння асиметрія;
д) має місце середня лівостороння асиметрія.
7. Значення коефіцієнта асиметрії складає (Кa = 0.72). Це свідчить про те, що розподіл:
а) симетричний;
б) має місце правостороння асиметрія;
в) має місце лівостороння асиметрія;
д) має місце висока правостороння асиметрія.
8. Розрахункове значення критерію Пірсона складає (7,8). При яких з наведених нижче критичних значень неможлива заміна емпіричного розподілу вибраним теоретичним:
а) 7,8;
б) 8,9;
в) 7,3;
г) 9,5.
9. Критичне значення критерію Колмогорова складає (5,6). При яких з наведених нижче розрахункових значень цього критерію заміна емпіричного розподілу вибраним теоретичним можлива:
а) 5,6;
б) 6,8;
в) 9,2;
г) 3,8.
Контрольні питання
1. Визначте поняття «показники варіації» та перелічить їх.
2. Розмах варіації: формула, недоліки.
3. Визначте поняття «альтернативна ознака» та покажіть, як визначається середня та дисперсія альтернативної ознаки.
4. Перелічіть види частот, які використовують для характеристики розподілу ознаки у сукупності, і вкажіть, які з них можуть бути використані для характеристики розподілу у інтервальних рядах з нерівними інтервалами.
5. Наведіть класифікацію форм розподілу значень ознаки в сукупності (по кількості вершин, симетричності, виду асиметрії, крутості розподілу).
6. Наведіть показники які в статистиці використовують для характеристики форми розподілу і покажіть яким чином форму розподілу можна охарактеризувати за допомогою середнього значення ознаки, моди або медіани.
7. Момент розподілу: поняття; формули для розрахунку (простий та зважений); види моментів розподілу.
8. Показники асиметрії та ексцесу: формули для розрахунку; характеристика форми розподілу.
9. Теоретичний розподіл: поняття; види теоретичних розподілів, які використовуються в економічних дослідженнях; ціль заміни фактичного розподілу теоретичним.
10. Критерій злагоди: поняття; покажіть яким чином за допомогою критерію Пірсона робиться перевірка гіпотези про припустимий закон невідомого розподілу.
11. Критерій злагоди: поняття; покажіть яким чином за допомогою критерію Колмогорова робиться перевірка гіпотези про припустимий закон невідомого розподілу.
Завдання для контрольної та самостійної роботи
5.1 Для одержаного в результаті виконання завдання 3.1 (тема 3) рівно-інтервального ряду розрахуйте абсолютні і відносні показники варіації виробництва продукції заводами галузі. Розрахунки представте в таблиці. Зробіть висновки.
5.2 Для одержаного в результаті виконання завдання 3.1 (тема 3) рівно-інтервального ряду розрахуйте дисперсію звичайним методом і за способом моментів. Розрахунки представте в таблиці. Зробіть висновки.
5.3 Для одержаного в результаті виконання завдання 3.1 (тема 3) рівно-інтервального ряду розрахуйте дисперсію за правилом складання дисперсій. Розрахунки представте в таблиці. Зробіть висновки.
5.4 Для одержаного в результаті виконання завдання 3.1 (тема 3) рівно-інтервального ряду розрахуйте асиметрію і ексцес розподілу обсягів виробництва підприємств галузі. Розрахунки представте в таблиці. Зробіть висновки.
5.5 Для одержаного в результаті виконання завдання 3.1 (тема 3) рівно-інтервального ряду перевірте гіпотезу про нормальний розподіл варіаційної ознаки за допомогою критеріїв згоди: а) Пірсона; б) Колмогорова. Розрахунки представте в таблиці. Зробіть висновки. Необхідні для вирішення завдання значення функції нормального нормованого розподілу та критеріїв Пірсона і Колмогорова наведені у додатку Г.

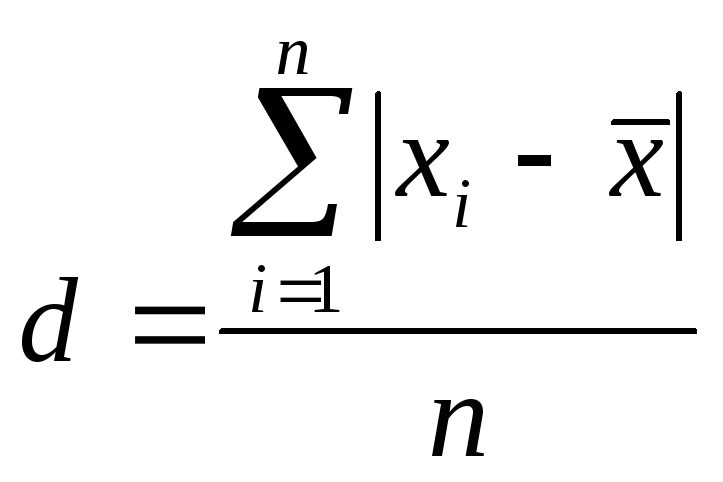 .
.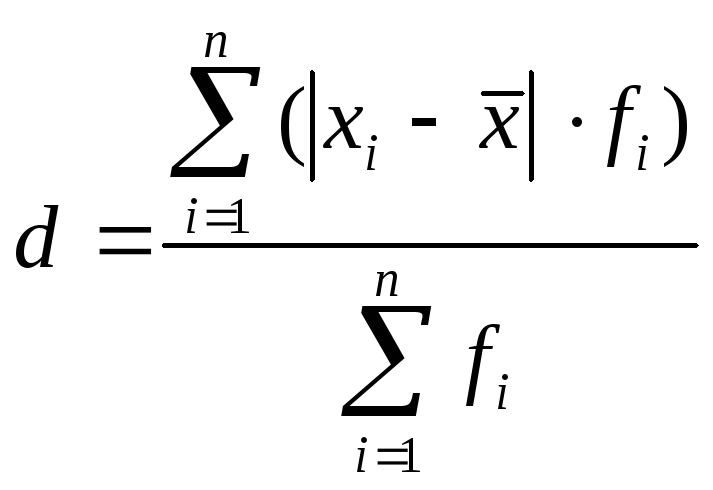 .
.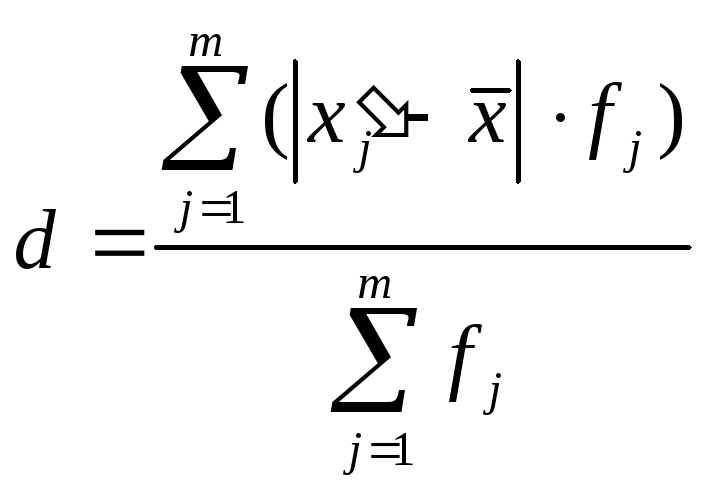 .
.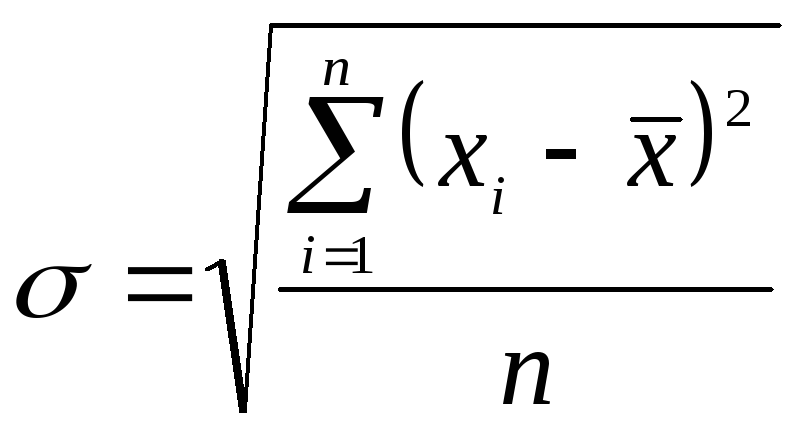 .
.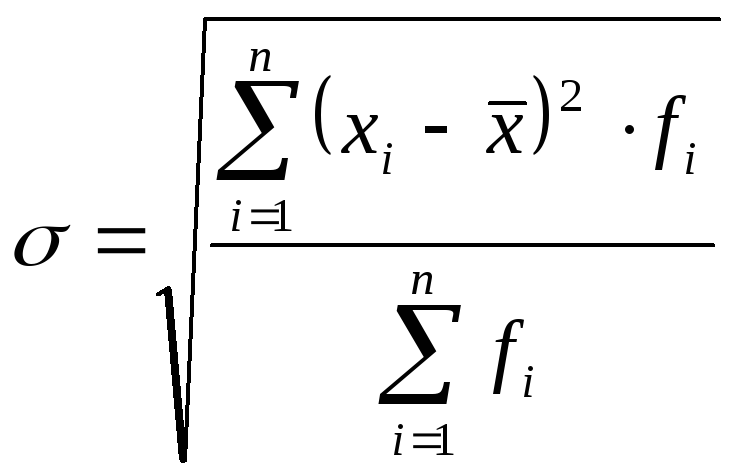 .
.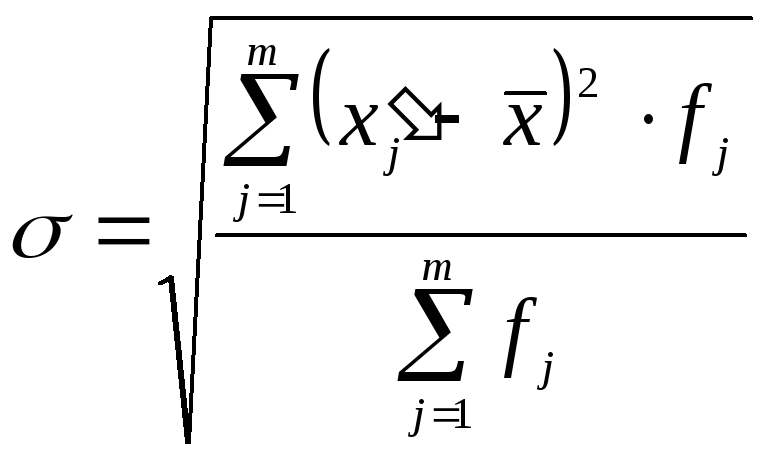 .
.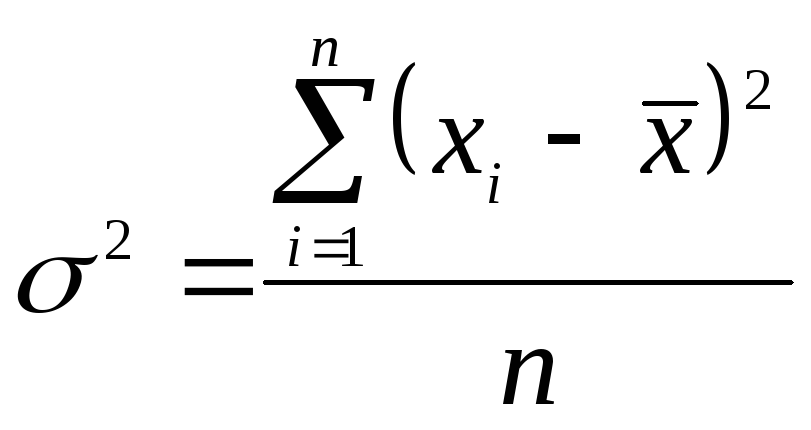 .
.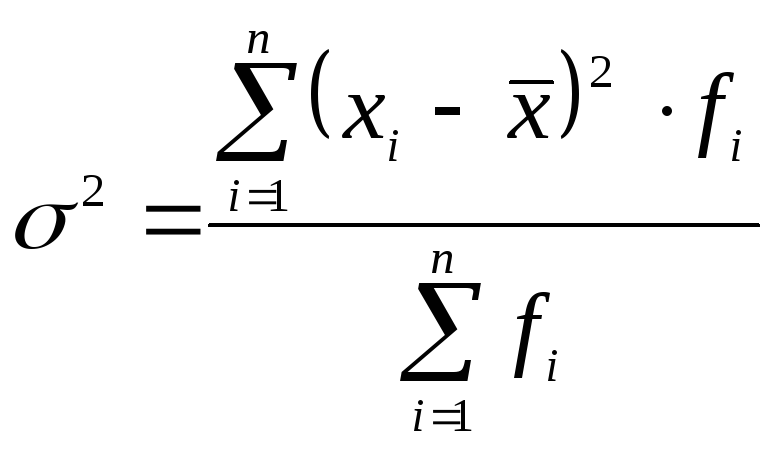 .
.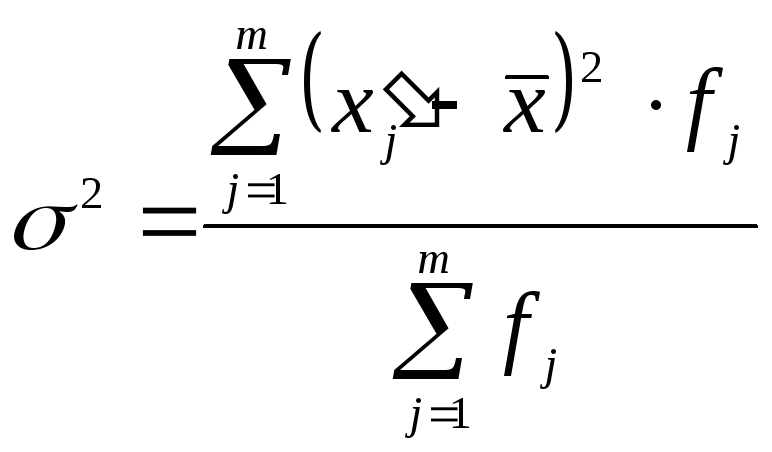 .
.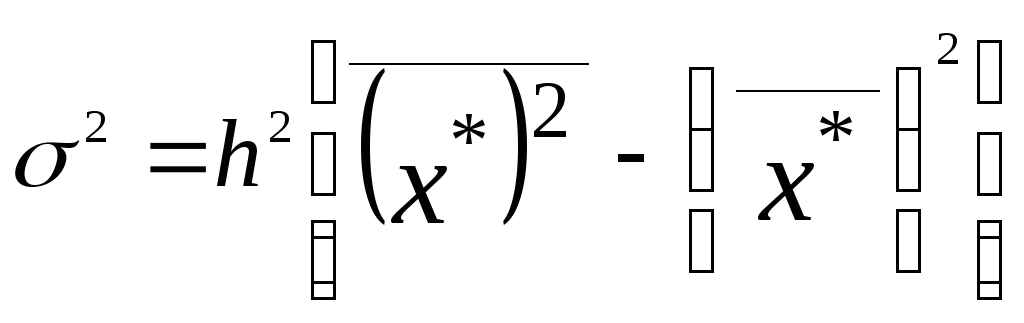 ,
,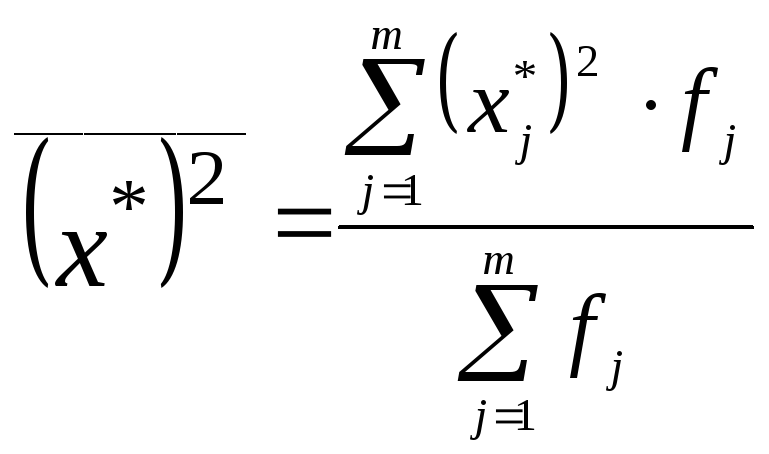 ,
,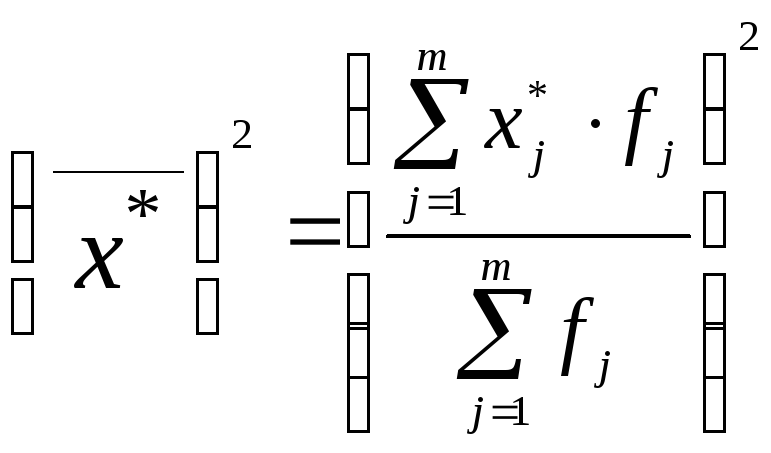 ,
,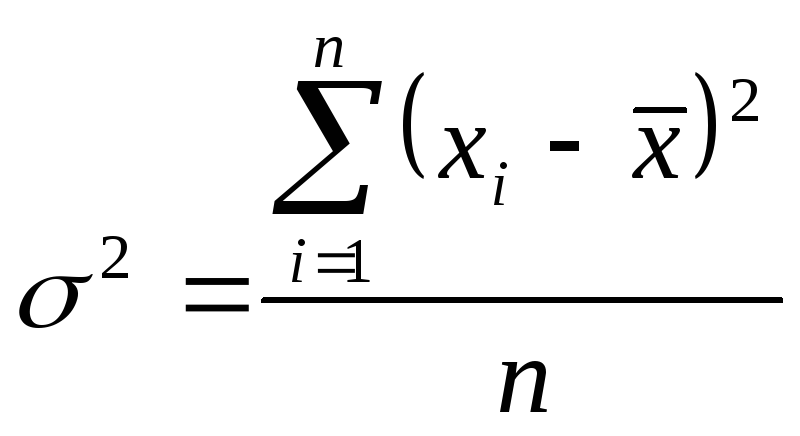 ,
,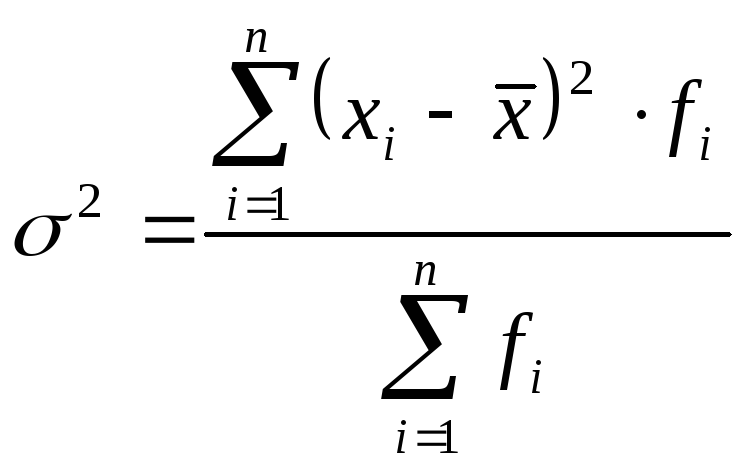 ,
,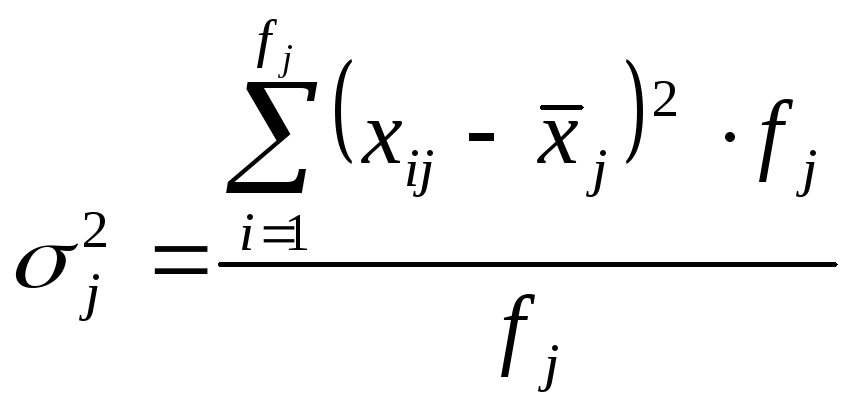 ,
,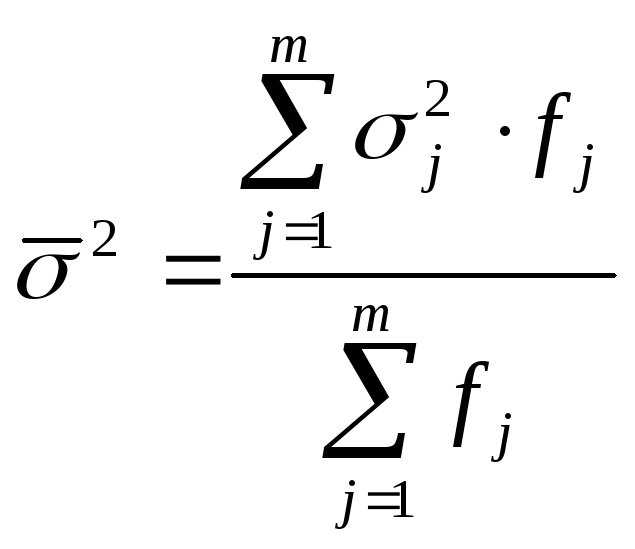 ,
,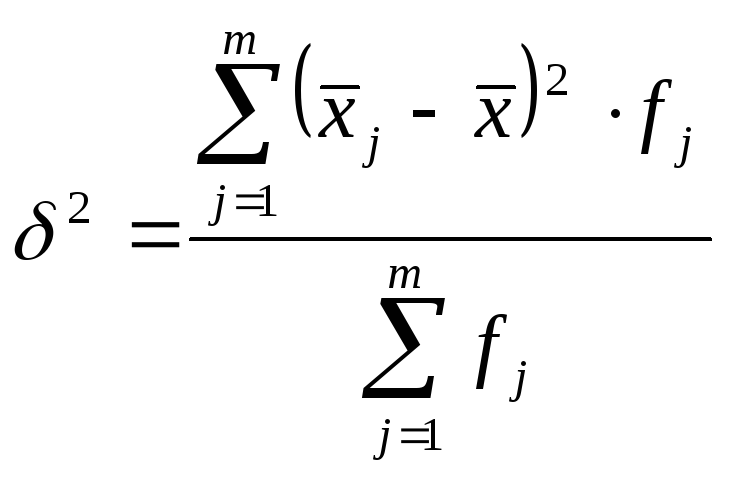 ,
,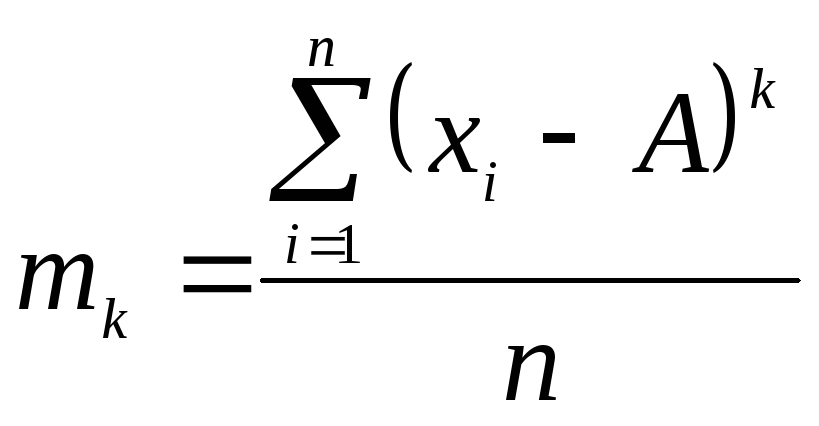 .
.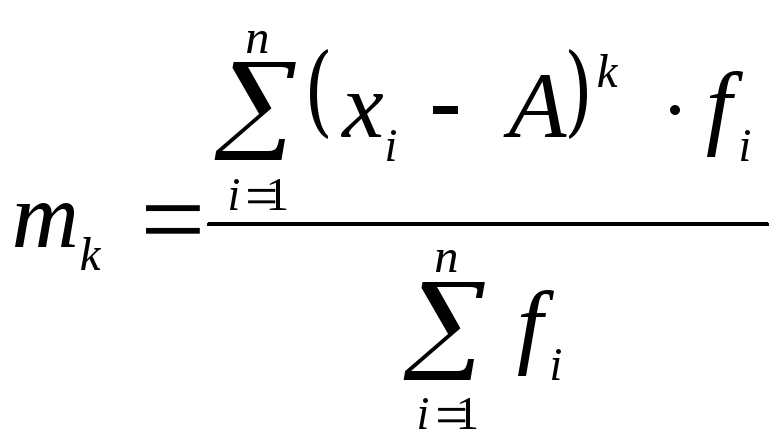 .
. .
.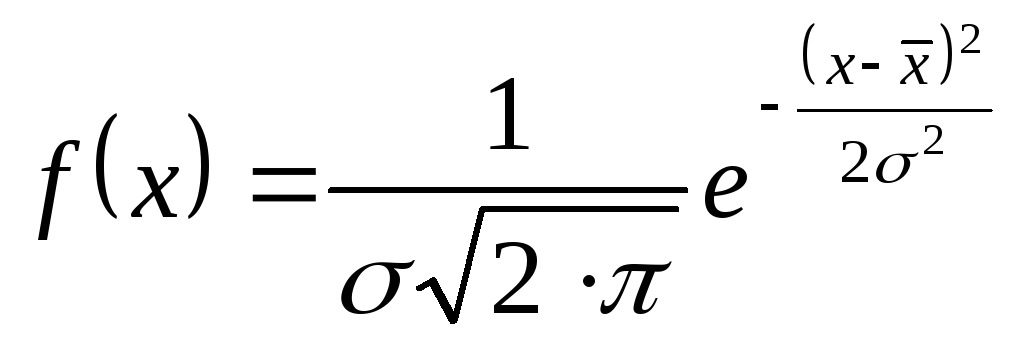 .
.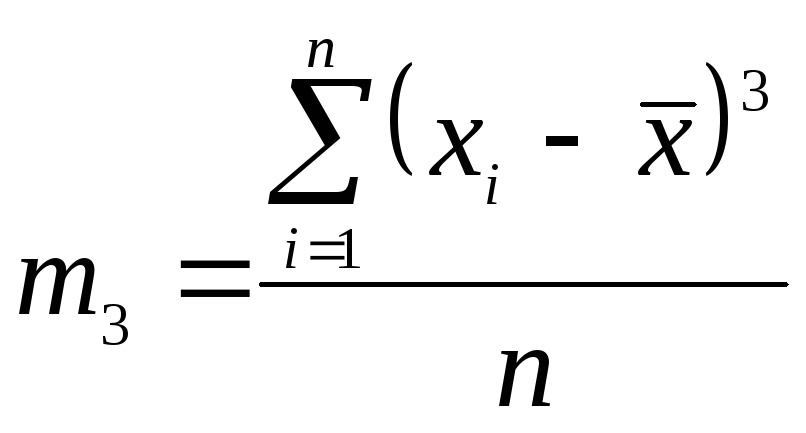 .
.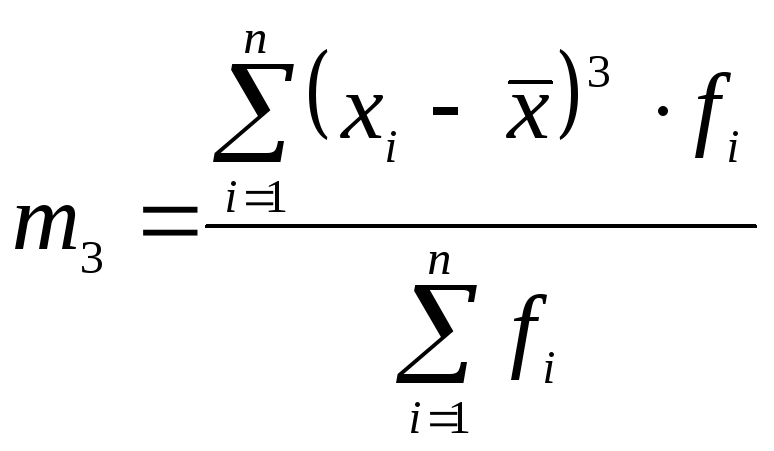 .
.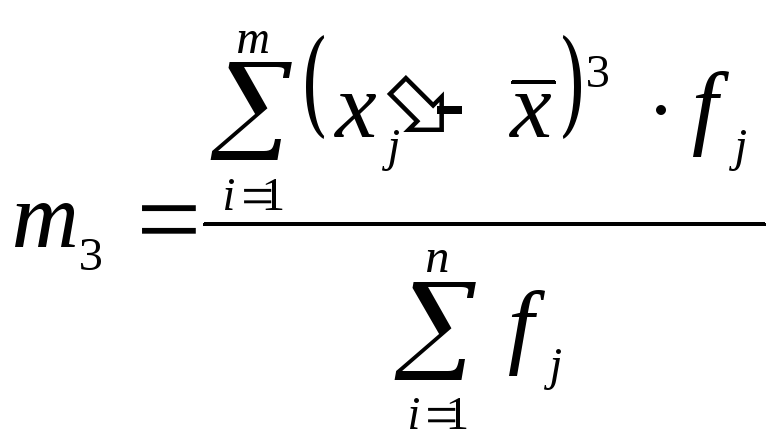 .
.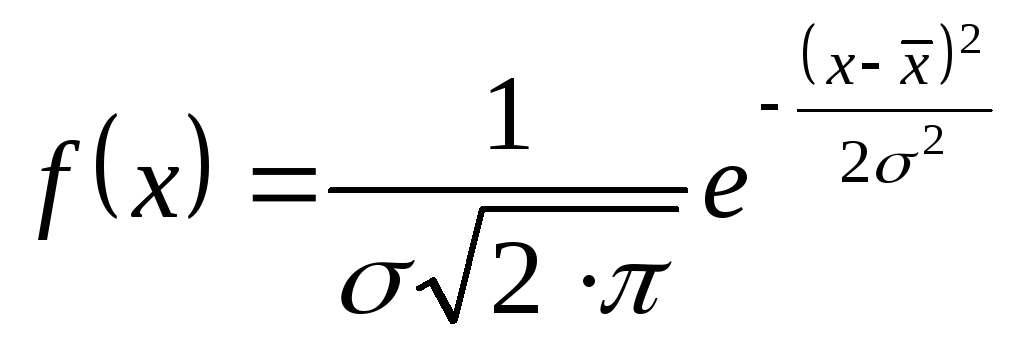 .
. ;
;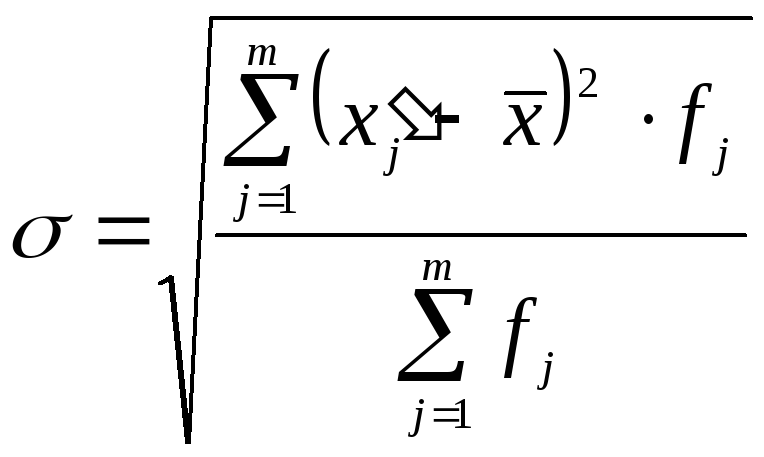 .
.