4.9. Индуктивное сопротивление Потье.

Опыт показывает, что опытная индукционная характеристика в действительности не совпадает с характеристикой построенной таким образом.

Причина заключается в том, что хотя для точки В' на ХХХ и для точки А' нагрузочной характеристики величины ЭДС Еfо одинаковы соответствующие токи возбуждения ОD < OK вследствие этого в режиме нагрузочной характеристики поток рассеивания обмоток возбуждения больше, что вызывает увеличение насыщения полюсов и ярма индуктора.

Поэтому при одинаковых Еfо в режиме нагрузочной характеристики в действительности необходимо увеличение тока возбуждения If на некоторую величину A'A". Рис. 4.6.

Поэтому для определения Xиспользуется не отрезок С'В', а отрезок С’ В">C'B'

Xp = C’B"/Iaн

Это сопротивление называется индуктивным сопротивлением Потье или расчетным индуктивным сопротивлением рассеивания обмотки якоря.

Для неявнополюсных машин Xp = 1.05 - 1.1 X,

для явнополюсных машин Xp = 1.1 - 1.3 X.

ЭМ.СM. 5.1. 08.01.06. 23.07.09. Отпечатано 30.09.10. 30.09.10

Тема 3. Синхронные машины.

Л е к ц и я 5. (30.09.10).

5.1. Диаграмма Потье.

При проектировании и эксплуатации синхронных машин возникает необходимость определения тока возбуждения, необходимого для обеспечения заданного режима работы ( U, I, COS). С этой целью для неявнополюсных генераторов пользуются диаграммой Потье, которая строится следующим образом.

Заданы U, I1, COS, R1 и X, ХХХи короткого замыкания.

1. На оси ординат откладываем номинальное напряжение машины Uн, и под углом отстающий номинальный ток якоря (статора)Iaн = Iн.

2. Определяем вектор суммарной ЭДС в якоре машины при нагрузке:

E = U + Ia*R1 + j Ia*X

где R1 активное сопротивление обмотки статора,

Х- индуктивное сопротивление рассеяния обмотки статора.

Эта ЭДС индуцируется результирующим потоком Фи определяет при этом степень насыщения машины в данном режиме.

3. Строим ХХХ Ef = f(If).

4. Повернув Eна угол получим точкуМ на оси ординат и по ней на ХХХ определяем необходимую ток возбуждения при нагрузке - Ifs, соответствующий полной МДС машины, необходимой для создания суммарного потока при нагрузке или суммарной ЭДС якоря машины при нагрузкеЕ- точкиM1иD.

Строим из точки 0 вектор тока возбуждения Ifs, опережающий векторЕна 90 градусов, точкаD’.

5. На ХХХ по ЭДС рассеяния статора E = Iaн*X,определяем ток возбуждения (МДС), необходимый для создания этой ЭДС -.отрезок0С.

6. Строим характеристику КЗ.

7. Для тока Iанпо характеристике КЗ определяем ток возбуждения необходимый для создания этого тока при коротком замыкании – отрезок0A.

8. Строим треугольник Потье АEС.

9. Определяем приведенный к обмотке возбуждения ток МДС реакции якоря Ifан’ (Ifан’ = Iaн *kid )( МДС реакции якоря Fad созданной током Iaн) в масштабе тока возбуждения - отрезокСАи откладываем его на направление тока Iа, от точкиD(точкаDсоответствует суммарная МДС возбуждения при нагрузке), отрезокDD1.[Пиотровский с. 417], [Вольдек с. 669].

kid– коэффициент приведения тока якоря к току возбуждения.

10. Поскольку полная МДС машины при нагрузке Ffsравна суме МДС индуктораFf и МДС реакции якоряFad:

ЭМ.СM. 5.2. 03.03.08. 23.07.09 30.09.10.

Ffs = Ff + Fad

Или в токах:

Ifs = If1 + Ifан'

Следовательно, ток возбуждения Ifн1для полученияU=Uнпри токеIaнравенIf1 = Ifs – Ifaн’, отрезокD10.

11. ЭДС Ef, создаваемая суммарным током возбуждения отстает на 90 град от токаIf1.

12. Величина этой ЭДС - Efопределяется по точкеNпересечения прямой, проведенной от точки 0 перпендикулярно току возбуждения при нагрузкеIf1, до пересечения с перпендикуляром к токуIа, проведенному из конца ЭДСEδ, точкаМ, т.е. с продолжением направление вектораj*Iaн*X.

Вектор MNравен ЭДС реакции якоряЕad= Xad*Ia, где Хad- насыщенное значение индуктивного сопротивления продольной реакции якоря, а вектор ОN - равен насыщенному значению ЭДСЕf, индуцируемой током возбужденияFfs.

Эта ЭДС соответствует насыщенной величине Ef-точкаN"определенной по спрямленной насыщенной характеристике ХХ проходящей через точкуМ1, т.е. с коэффициентом насыщения соответствующим точкеМ1ХХХ.

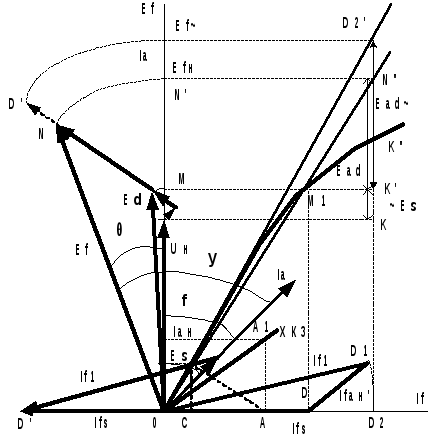Диаграмма Потье приведена на рис. 5.1.

Рис. 5.1. Диаграмма Потье, совмещенная с ХХХ.

ЭМ.СM. 5.2.a. 02.02.2001. 12.03.2005.