Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ухтинский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

posobia_4semФизика / Квантовая оптика _пособие_

.pdf

Скачиваний:

314

Добавлен:

02.03.2016

Размер:

831.28 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 166 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Дано:	Си:	Решение:
Дано:	Си:	Решение:
100 пм	10 10 м		’
180			’
180				P

?
?				e
				e

Рис. 3

Энергия электрона отдачи равна разности энергий падающего и рассеянного фотонов:

					' h h ' h												c		h		c	hc			,	(1)
					' h h ' h														h		'	hc			,	(1)
																					'			'
где	'			- изменение длины волны фотона в результате рассеяния на
свободном электроне:
														2h		sin2				,						(2)
														m0c		sin2			2	,						(2)
														m0c					2
где:	m0	9,11 10 31 кг - масса покоя электрона;
	h 6,63 10 34 Дж ·с - постоянная Планка.
	Подставив (2) в (1) и учитывая, что ' , найдем искомую энергию
электрона отдачи:
				2h	sin		2
				2h	sin
								2				.
						2h				2		.
			m0					sin
			m0			m0c		sin
						m0c					2
	Вычисляя, получим:
								2 (6,63 10 34 )2							sin2				180
								2 (6,63 10 34 )2							sin2					2
																				2
														2 6,63 10 34											180
														2 6,63 10 34											180
			9,11 10 31 10 10						10 10															sin2
			9,11 10 31 10 10						10 10				9,11		10			31		3 10			8	sin2	2
													9,11		10					3 10					2
9,2 10 17 (				575 (эВ).
	Ответ: 575 эВ.

Задача 3.

В результате эффекта Комптона фотон при соударении с электроном был рассеян на угол 90 (рис. 4). Энергия рассеянного фотона равна 0,4 МэВ. Определить энергию фотона до рассеяния.

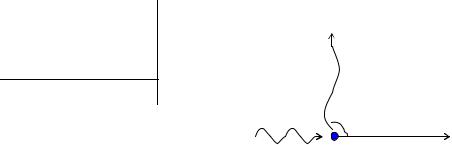
Дано:	Си:	Решение:
0,4 106 эВ		’
90

Рис. 4

Для определения энергии первичного фотона воспользуемся формулой Комптона в виде:

' 2	2	sin2	.	(1)

	mc		2

Формулу (1) преобразуем следующим образом:

1.выразим длины волн 'и через энергии ' и соответствующих фотонов, воспользовавшись соотношением: 2 hc ;

2.умножим числитель и знаменатель правой части формулы на c (скорость света). Тогда получим:

2 c 2 c			2 c 2sin2		.
			mc2		2
Сократив на 2 c , выразим из этой формулы искомую энергию:
				'mc2				'E		,	(2)
								0		,	(2)
								0
				mc2 '2sin2			E0 2 'sin2
					2				2
где	E mc2	0,51МэВ -			энергия	покоя		электрона (во			внесистемных
	0

единицах). Вычисления по формуле (2) удобнее вести во внесистемных единицах.

Подставив числовые данные, получим:

	0,4 106 0,51 106								1,85 (МэВ).
	10	6	2	0,4 10	6	sin	2	90	1,85 (МэВ).
0,51	10		2	0,4 10		sin		2
								2
Ответ: 1,85				МэВ.

Задача 4.

Определить угол (рис. 5), на который был рассеян квант с энергией 2,04 МэВ при эффекте Комптона, если кинетическая энергия электрона отд ачи Т равна 1,02 МэВ.

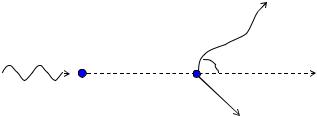
Дано:

Си:

Решение:

2,04 10 6 эВ

3,3 10 13 Дж

’

T 1,02 106 эВ

1,6 10 13 Дж

Рис. 5

Угол рассеяния можно определить из формулы Комптона:

1 cos .

(1)

m c

где

- длина волны падающего фотона,

- длина волны рассеянного

фотона, m0 - масса электрона.

Энергия фотона определяется из формулы:

hc , где

(2)

h - постоянная Планка, c - скорость света.

Тогда

hc .

(3)

С учетом того, что T выражение (1) представим в виде:

1 cos ,

m c2

m c2T

T 1 cos ,

cos 1

m c2T

Произведем вычисления:

9,11 10 31 3 108 2 1,6 10 13

cos 1

0,75,

3,3 10 13 1,6 10 13 3,3 10 13

arccos0,75 41 30' .

Ответ: 41 30' .

Задача 5.

Определить импульс электрона отдачи Pe , если фотон с энергией 1,02 МэВ в результате рассеяния потерял половину своей энергии.

Дано:	Си:	Решение:
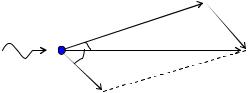
Дано:	Си:	Решение:
1,02МэВ				P	Pe
E0 0,51МэВ			e	P	Pe
E0 0,51МэВ			e		P
0,5 0,51 МэВ
c 3 108 м/с		P
c 3 108 м/с		P	m
		e
Pe ?				Рис. 6

По закону сохранения импульса имеем: импульс падающего фотона P равен векторной сумме импульсов рассеянного фотона P и электрона отдачи m (рис. 6):

P P m ,	(1)

где P c и P c .

Из выражения (1) найдем импульс электрона: m P P или

Pe P P .

Для нахождения импульса электрона найдем угол рассеяния . Используем формулу Комптона:

2	h	sin2 .
2	m c	sin2 .
	m c	2
	0

Заменим длину волны через энергию ( hc ), получим:

2sin2

;

m c

2sin2

;

m c2

2sin

где h – постоянная Планка,

c – скорость света в вакууме,

– длина волны падающего фотона,

– длина волны рассеянного фотона,

– угол рассеяния.

По условию:

0,5 , Следовательно,

1	1	2sin	2
			2	;
0,5		E

		0

11 cos ;

1 cos						E0				; (т.к.					2sin2			1 cos ).
1 cos										; (т.к.					2sin2			1 cos ).
																	2
Следовательно cos 1																		E0			;
Следовательно cos 1																					;

Импульс электрона Pe																	найдем по теореме косинусов:

P				P		2 P2 2P P cos ;
e

			2					2											E0
Pe											2						1						;
Pe			c2					c2			2				c2		1						;
			c2					c2							c2

		1 1																		E0						1						1
		1 1					2					2								E0						1		5	2	2		1		1		2
Pe													2				1														E0							E0
Pe		c 4											2				1									c 4					E0	c		4				E0	.
		c 4														2										c 4						c		4					.
Подставим численные значения:
		1																					10		8							10 8
									1,02				2
P									1,02					0,51 1,02													0,2601 0,5202								0,88 (МэВ)
P		3 108												0,51 1,02													0,2601 0,5202								0,88 (МэВ)
e											4													3									3
											4													3									3
P 0,47 10 21(																	.
e
Ответ:					P 0,47 10 21																	.
					e
	Рекомендуемые задания для внеаудиторного рассмотрения
1. Рентгеновское излучение длиной волны																															55,8			пм			рассеивается
плиткой	графита									(Комптон -								эффект). Определить длину																волны				' света,
рассеянного под углом 60 к направлению падающего пучка света.
Ответ: = 57 пм.

2. Определить максимальное изменение длины волны при комптоно вском рассеянии: 1) на свободных электронах; 2) на свободных прот онах.

Ответ: 1) λmax,е = 4,85 пм; 2) λmax,р = 2,64 фм.

3. Определить угол рассеяния фотона, испытавшего соударение со свободным электроном, если изменение длины волны при рассеянии равно 3,62 пм.

Ответ: θ = 120 или 240 .

4.Фотон с энергией 0,4 МэВ рассеялся под углом 90 на свободном электроне. Определить энергию рассеянного ' фотона и кинетическую энергию T электрона отдачи.

Ответ: = 0,224 МэВ = 0,36 10-13 Дж, Т = 0,176 МэВ = 0,28·10-13 Дж.

5.Определить импульс pe электрона отдачи при эффекте Комптона, е сли фотон с энергией , равной энергии покоя электрона E0 , был рассеян на угол

180 .

Ответ: ре = 3,63·10 -22 кг·м/c.

6. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол 180 ? Энергия фотона до рассеяния равна 0,255 МэВ.

Ответ: T 0,5 .

7.Фотон с энергией 0,25 МэВ рассеялся на свободном электроне. Энергия ' рассеянного фотона равна 0,2 МэВ. Определить угол рассеяния .

Ответ: θ = 60 43,5' или 299 16,5'.

8.Угол рассеяния фотона равен 90 . Угол отдачи электрона равен 30 .

Определите энергию падающего фотона. Ответ: ε = 0,37 МэВ.

9. Фотон ( 1пм) рассеялся на свободном электроне под углом		90 .
Какую долю своей энергии фотон передал электрону?
Ответ: 70,8%.
10.Длина волны фотона	равна комптоновской длине c электрона.
Определить энергию и импульс	p фотона.

Ответ: = 0,512 МэВ, р = 2,7∙10-22 кг м/с .

11.Энергия падающего фотона равна энергии покоя E0 электрона. Определить долю 1 энергии падающего фотона, которую сохранит рассеянный фотон, и долю 2 этой энергии, полученную электроном отдачи,

если угол рассеяния равен: 1) 60 ; 2) 90 ; 3) 180 .

Ответ: 1) 1 0,67 , 2 0,33; 2) 1 2 0,5; 3) 1 0,33, 2 0,67 .

12.Фотон с длиной волны 100 пм рассеялся под углом 180 на свободном электроне. Определить в электрон -вольтах кинетическую энергию электр она отдачи.

Ответ: Т = 575 эВ.

13.Фотон рентгеновского излучения с э нергией 0,15 МэВ испытал рассеяние

на покоившемся	свободном	электроне,	в результате	ч его	его длина волны
увеличилась на	0,015	0	угол ,	под	которым вылетел
		. Найти

комптоновский электрон отдачи. Ответ: φ = 49,1º.

Домашнее задание

1. Составить ответы на контрольные вопросы. 2.Решить следующие задачи:

1. При комптоновском рассеянии энергия падающего фотона распределяется поровну между рассеянным фотоном и электроном отдачи.

Угол рассеяния 2 . Найти энергию и импульс p рассеянного фотона. Ответ: ε΄ = 260 кэВ; р΄ = 1,37·10 –22 кг·м /c.

2. Энергия рентгеновских лучей 0,6 МэВ. Найти Te энергию электрона отдачи, если длина волны рентгеновских луч ей после комптоновского рассеяния изменилась на 20%.

Ответ: Т = 0,1 МэВ.

3. Рентгеновские	лучи	с	длиной	волны		70,8	пм	испытывают
комптоновское рассеяние на парафине. Найти длину волны							' рентгеновских
лучей, рассеянных в направлениях: а)					; б) .
лучей, рассеянных в направлениях: а)				2	; б) .
				2
Ответ: а) = 73,22 пм; б) = 75,7 пм.
4. Рентгеновские	лучи	с	длиной	волны		20	пм	испытывают
комптоновское рассеяние под			углом 90 . Найти изменение					длины

волны рентгеновских лучей при рассеянии, а также энергию электрона отдачи

T и его импульс pe .
Ответ: = 2,42 пм; Т = 6,7 кэВ; p	e	= 4,48·10 –23	кг м/с .
	e

Практическое занятие 5 АТОМ ВОДОРОДА ПО ТЕОРИИ БОРА

1.Поясните строение атома по теории Бора. Разъясните смысл постулатов Бора. Как с их помощью объясняется линейчатый спектр атома?

2.Запишите выражение для энергии фотона, излучаемого атомом водорода при переходе из одного стационарного состояния в другое. Поясните, что такое энергия ионизации Ei атома водорода.

3.Запишите и поясните формулу, определяющую длину волны света, излучаемого или поглощаемого атомом водорода при переходе электрона с одной орбиты на другую.

4.Почему из различных серий спектральных линий атома водорода первой была изучена серия Бальмера?

5.Какой смысл имеют числа n1 и n2 в обобщённой формуле Бальмера?

Литература: Т. Гл. 27, § 208-212, С. 386-393, 2000.

Примеры решения задач

Задача 1.

Вычислить радиус первой орбиты атома водорода (боровский радиус) и

скорость электронов на этой орбите.
Дано:		Си:	Решение:				радиус r
Дано:		Си:	Решение:
n 1			Согласно		теории	Бора,
1,05 10 34	Дж·с		электронной орбиты и скорость электрона на
e 1,6 10 19 Кл			ней связаны равенством			m r n . Так как в
m 9,11 10 31	кг		задаче	требуется определить			величины,
0 8,85 10 12 Ф/м			относящиеся к		первой	орбите,	то главное
0 8,85 10 12 Ф/м			квантовое число n 1 и равенство примет вид
			квантовое число n 1 и равенство примет вид
					m r .		(1)
r1 , ?					m r .		(1)
r1 , ?			Для	определения		двух	неизвестных
			Для	определения		двух	неизвестных

величин r и необходимо ещё одно уравнение. В качестве второго уравнения воспользуемся уравнением движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщают электрону центростремительное ускорение. На основании второго закона Нь ютона можем записать:

	m 2			1		e2 ,
	r					e2 ,
	r			4 0 r2
где e и m - заряд и масса электрона, или
									m		2		1		e2 .	(2)
									m		2				e2 .	(2)
													4 0 r
Совместное решение равенств (1) и (2) относительно																r даёт:
r		4 0 2			,
r			me2		,
где 1,05 10 34 Дж·с – постоянная Планка.
Подставив сюда значения											, e ,			m , 0 и произведя вычисления, найдём
боровский радиус:
		4 3,14 8,85 10						12	1,05		10		34	2
		4 3,14 8,85 10							1,05		10
r															5,29 10 11 (м).
r															5,29 10 11 (м).
1				9,11 10			31		10	19		2
1							31	1,6		19		2
								1,6

Из равенства (1) получим выражение скорости электрона на первой орбите:

mr .

Произведя вычисления по этой формуле, найдём :

		1,05 10 34				2,18 (Мм/с).
	9,11 10		31	5,29 10	11

Ответ:		r 5,29 10 11			м, 2,18 Мм/с.
		1

Задача 2.

Определить энергию фотона, соответствующего второй линии в пе рвой инфракрасной серии (серии Пашена) атома водорода.

	Дано:	Решение:
	Дано:	Решение:
n1	3	Энергия		фотона, излучаемого атомом водор ода при
Ei	13,6 Эв	переходе электрона с одной орбиты на др угую:
		1		1
		1		1
?		E			,
?		E
		i n2		n2
			1	2

где Ei энергия ионизации атома водорода;

n1 1,2,3,... номер орбиты, на которую переходит электрон (рис. 1); n2 n1 1; n1 2; ...; n1 m номер орбиты, с которой переходит электрон;

<<< < Предыдущая 1 2 3 4 56 / 166 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в папке posobia_4semФизика

#
02.03.2016831.28 Кб314Квантовая оптика _пособие_.pdf
#
02.03.20161.54 Mб2047Квантовая оптика _решебник_.pdf