posobia_4semФизика / Квантовая оптика _пособие_

1 U0 1 . E 1

Возведя обе части равенства в квадрат, найдем высоту потенциальной ступени:

Подставив сюда значения величин и произведя вычисление, найдем:

U0 = 55,6 эВ.

Ответ: U0 = 55,6 эВ.

Задача 3. Электрон с энергией Е = 4,9 эВ движется в положительном направлении оси x (рис. 4). Высота U0 потенциальной ступени равна 5 эВ. При какой шине d ступени вероятность W прохождения электрона через нее будет равна 0,2?

Для удобства вычислений изменим знак у правой и левой части этого равенства и найдем d:

Входящие в эту формулу величины выразим в единицах СИ и произв едем вычисления:

d = 4,95∙10-10 м = 0,495∙10-9 м = 0,495 нм.

91

Учитывая, что формула (4) приближенная и вычисления носят оцено чный характер, можно принять d = 0,5 нм.

Ответ: d = 0,5 нм.

Задача 4. Электрон находиться в одномерном потенциальном ящике шириной l (см. рис. 1). Определить среднее значение координаты <x> электрона (0<x<l).

где ψ(х) - нормированная на единицу собственная ψ - функция. В случае бесконечно глубокого прямоугольного потенциального ящика ψ - функция имеет вид:

Следовательно:

из известной формулы дифференцирования (пр оизводной): (uv)΄ =u΄v + v΄u.

92

Следовательно, среднее значение координаты:

Задача 5. Атом водорода находиться в состоянии 1 s. Определить вероятность W пребывания электрона в атоме внутри сферы радиусом r = 0,1a (где a-радиус первой боровской орбиты). Волновая функция, описывающая это состояние, считается известной.

где 1,0,0 r - собственная нормированная волновая функция, отвеч ающая

Благодаря сферической симметрии функция ψ вероятность обнаружить электрон на расстоянии r одинакова по всем направлениям. Поэтому эл емент объема dV, отвечающий одинаковой плотности вероятности, можно представить в виде объема сферического слоя радиусом r и толщиной dr: dV = 4πr2dr.

С учетом выражений 1,0,0 r и dV формула (1) запишется в виде:

При вычислении вероятности удобно перейти к атомным единицам, приняв качестве единицы длинны радиус первой боровской орбиты a. Если ввести безразмерную величину x = r/a, то:

r2 = (xa)2, dr = adx и dW 4e 2 х x2dx .

93

Вероятность найдем, интегрируя dW в пределах от r1 = 0 до r2 = 0,1a (или от x1 = 0 до x2 = 0,1):

Этот интеграл может быть точно вычислен интегрированием по частям, однако при малых х (хmax = 0,1) выражение e-2x можно разложить в ряд Маклорена:

e 2 x 1 2x 21! 2x2 и произвести приближенное вычисление.

Пренебрегая всеми членами степени выше первой, запишем интеграл в

виде:

Ответ: W = 1,13·10-3.

Задача 6. Электрон в возбужденном атоме водорода находиться в 3р - состоянии. Определить изменение магнитного момента, обусловленного орбитальным движением электрона, при переходе атома в основное состояние.

состоянии l2 = 1 и Мl1 = B 2 . Следовательно, изменение магнитного м омента: Мl = 0 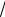– B 2 = B 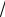2 ≈ – 0,927·10-23 · 1,41 = – 1,31·10-23 Дж/Тл.

Знак минус показывает, что в данном случае магнитный момент уменьшился.

Ответ: Мl = – 1,31·10-23 Дж/Тл.

94

Рекомендуемые задания для внеаудиторного рассмотрения

1. Функция вида (x) C sin( n x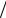L) является волновой функцией, описывающей состояние (с квантовым числом n) частицы, движущейся вдоль оси x в одномерной бесконечно глубокой потенциальной яме шириной L. Используя условие нормировки, определите велич ину коэффициента С.

Ответ: C L2 .

2.Частица в потенциальном ящике находится в основном состоянии. Какова вероятность W нахождения частицы: 1) в средней трети ящика; 2) в крайней трети ящика?

Ответ: 1) W1 = 0,609; 2) W2 = 0,195.

3.Атом водорода находится в основном состоянии. Собственная волновая

функция, описывающая состояние электрона в атоме, имеет вид

r

(r) Ce a , где С некоторая постоянная. Найти из условия нормировки постоянную С.

Определить расстояние r, на котором вероятность нахождения электрона максимальна.

Ответ: r = а = 52,6 пм.

5.Электрон в атоме находится в f – состоянии. Найти орбитальный момент

импульса Lℓ электрона и максимальное значение проекции момента импульса (Ll,z)max на направление внешнего магнитного поля .

Ответ: Lℓ = 3,64∙10-34 Дж∙с; (Lℓ,z)max = 3,15∙10-34 Дж∙с.

95

6.Момент импульса Lℓ орбитального движения электрона в атоме водорода равен 1,83∙10-34 Дж∙с. Определить магнитный момент Мℓ электрона, находящегося в 2р-состоянии в атоме водорода.

Ответ: рmℓ = Мℓ = 1,61∙10-23 Дж/Тл.

7.Вычислить спиновый момент импульса Ls электрона и проекцию Ls,z этого момента на направление внешнего магнитного п оля.

Ответ: Ls = 0,909∙10-34 Дж∙с, Ls,z = 0,525∙10-34 Дж∙с.

8.Вычислить спиновый магнитный момент Ms электрона и проекцию магнитного момента Ms,z на направление внешнего магнитного поля.

Ответ: pms = Ms = 1,61∙10-23 А∙м2, pmsz =Ms,z = 9,274∙10-24 А∙м2.

9.Используя принцип Паули, указать, какое максимальное число Nmax электронов в атоме могут иметь одинаковыми следующие квантовые

числа: 1) n, ℓ, mℓ, ms; 2) n, ℓ, mℓ; 3) n, ℓ; 4) n.

Ответ: 1) Nmax = 1; 2) Nmax = 2; 3) Nmax.= 2(2ℓ + 1); 4) Nmax.= 2n2.

10.Найти число N электронов в атомах, у которых в основном состоянии заполнены: 1) K- и L-слои, 3s-оболочка и наполовину 3р-оболочка; 2) K-, L- и М- слои и 4s, 4р и 4d-оболочки. Что это за атомы?

Ответ: 1) N = 15, атом фосфора; 2) N = 46, атом палладия.

Домашнее задание

1.Составить конспект ответов на вопросы.

2.Решить следующие задачи:

1.Частица в потенциальном ящике шириной L находится в возбуждённом состоянии (n = 2). Определить в каких точках интервала ( 0 < x < L) плотность

вероятности |ψn(x)|² нахождения частицы максимальна и минимальна. Ответ: 1) максимумы: х1 = L/4, х3 = 3L/4; 2) минимум: х2 = L/2.

2.Вычислить момент импульса Lℓ орбитального движения электрона, находящегося в атоме: 1) в s – состоянии; 2) в р – состоянии.

Ответ: 1) Lℓ.= 0; 2) Lℓ.= 1,48∙10-34 Дж∙с.

96

3. Определить возможные значения проекции момента импульса Lℓz орбитального движения электрона в атоме на направление внешнего магнитного поля. Электрон находится в d –состоянии.

Ответ: 1) Lℓz.= 0; 2) Lℓz.= ± 1,05∙10-34 Дж∙с, 3) Lℓz.= ±2,1∙10-34 Дж∙с.

4.В атоме K, L и M оболочки заполнены полностью. Определите общее число электронов в атоме.

Ответ: N =28.

5.Считая, что «нарушений» в порядке заполнения электронных оболочек нет, записать электронные конфигурации атома с атомным номером Z = 36.

Ответ: 1s22s22p63s23p63d104s24p6.

97

РАЗДЕЛ II. ЭЛЕМЕНТЫ ФИЗИКИ АТОМНОГО ЯДРА

Практическое занятие 10 1. МАССА, РАЗМЕР, СОСТАВ И ЗАРЯД АТОМНОГО ЯДРА.

МАССОВОЕ И ЗАРЯДОВОЕ ЧИСЛО

1.Что такое атомная масса Ar (относительная атомная масса), атомная единица массы (а.е.м.)?

2.Из каких частиц состоит атомное ядро?

3.Какой заряд имеет протон (p) и чему равна масса протона (mp)? Запишите символическую запись протона.

4.Имеет ли заряд нейтрон (n), чему равна масса нейтрона (mn)? Запишите символическую запись нейтрона.

5.Что называют нуклонами?

6.Что называют массовым числом A?

7.Что называют зарядовым числом Z и что определяет заряд ядра?

8.Как символически обозначается ядро?

9.Объясните отличие изотопов и изобаров.

10.Имеют ли ядра атомов резко выраженные границы? 11.Запишите эмпирическую формулу для радиуса ядра. 12.Чему равна плотность ядерного вещества.

Литература: Т., Гл. 32, §§251, 256 – 259, 262, 264, С. 466 – 467, 2000.

Примеры решения задач

Задача 1.

Определите массу нейтрального атома 2452Сr .

массе атома углерода 126 С, которая принимается равной 12,000000.

Для абсолютного определения относительной атомной массы была введена атомная единица массы (а.е.м.).

Атомная единица массы (а.е.м.) равна 112 массы атома углерода 126 C .

98

Отсюда следует, что углерод обладает относительной атомной массой Ar =12,000 и абсолютной атомной массой m=12,000 (а.е.м.). Атомную единицу массы можно перевести в единицу массы СИ – килограмм.

Формула (2) используется также для определения массы ядер, элементарных частиц, частиц – продуктов радиоактивных превращений и т.д. Тогда в нашем случае, согласно (2), масса нейтрального атома 2452Сr :

ma = 52ּ1,66057ּ10-27(кг) = 8,63ּ10 -26(кг). Ответ: ma = 8,63ּ10-26кг.

Задача 2.

Чем отличается массовое число от относительной массы ядра?

Ответ: Массовое число – число нуклонов в ядре, поэтому оно всегда целое. Относительная масса ядра определяется отношением массы ядра к 112 массы изотопа углерода 12C . Это число целым быть не может.

Задача 3.

Водород обогащен дейтерием. Определить массовые доли ω1 протия и ω2

где m1 и m2 -массы соответственно протия и дейтерия в смеси. Выразим из этих равенств массы m1 и m2:

m1 1 (m1 m2 ) ; m2 2 (m1 m2 )

иподставим их в знаменатель формулы, определяющей молярную ма ссу

Мсмеси:

99

Так как молярные массы протия и дейтерия пропорциональны их относительным атомным массам, то равенство (1) можно переписать в виде

дейтерия.

Заметим далее, что сумма массовых долей всех компонентов должна быть равна единице, т.е.

ω1 + ω2 = 1. (3) Решив совместно равенство (2) и (3), найдем

В таблице №12 (стр. 135) найдем: атом водорода Ar1 = 1,00783, атом дейтерия Ar2 = 2,01410.

Подставив числовые значения величин в (4), получим:

ω1 = 0,796 и ω2 = 0,204. Ответ: ω1 = 0,796, ω2 = 0,204.

100