
- •Оглавление
- •Закон Кулона. Экспериментальные проверки закона Кулона. Теорема Остроградского-Гаусса. Дифференциальная формулировка закона Кулона.
- •Классическая теория электропроводности и ее затруднения. Объяснение законов Ома, Джоуля-Ленца, Видемана-Франца на основе классической электронной теории.
- •Объяснение закона Джоуля-Ленца с точки зрения классической электронной теории
- •Закон взаимодействия элементов тока (закон Лапласа-Био-Савара-Ампера). Полевая трактовка закона взаимодействия элементов тока. Релятивистская природа магнитного поля.
- •Нахождение электрического поля с использованием потенциала, прямым применением закона Кулона и с использованием теоремы Гаусса.
- •Закон Био-Савара. Вектор магнитной индукции. Закон Ампера.
- •Закон Ампера
- •Зависимость электропроводимости от температуры, явление сверхпроводимости.
- •Емкость уединенного проводника. Система проводников. Конденсаторы и их емкость. Общая задача электростатики. Понятие о методе изображений для решения некоторых электростатических задач.
- •Теорема о циркуляции вектора магнитной индукции в стационарном случае. Вихревой характер магнитного поля.
- •Электростатическое поле при наличии диэлектриков. Поляризация. Связанные и свободные заряды. Электростатическая теорема Гаусса при наличии диэлектриков.
- •Понятие о зонной теории твердых тел. Расщепление энергетических уровней и образование зон. Энергетические зоны металлов, полупроводников и изоляторов.
- •Электрическое смещение и диэлектрическая проницаемость. Преломление силовых линий на границе раздела диэлектриков.
- •Собственная проводимость полупроводников. Примесная (электронная и дырочная) проводимость. Доноры и акцепторы. Температурная зависимость проводимости полупроводников.
- •Энергия электростатического поля. Энергия взаимодействия при непрерывном распределении зарядов. Собственная энергия.
- •Индукции токов в движущихся проводниках. Закон электромагнитной индукции Фарадея.
- •Объемная плотность энергии электрического поля. Энергия поля поверхностных зарядов. Энергия заряженных проводников.
- •Энергия заряженных проводников
- •Цепи квазистационарного переменного тока. Цепь с источником переменных сторонних эдс, сопротивлением, емкостью, и индуктивностью.
- •Силы в электрическом поле. Силы, действующие на точечный заряд, диполь и непрерывно распределенный заряд. Силы, действующие на диэлектрик и проводник. Энергетический метод определения сил.
- •Закон электромагнитной индукции Фарадея. Дифференциальная формулировка закона электромагнитом индукции Фарадея.
- •Энергия диполя во внешнем поле.Поле диполя
- •Метод векторных диаграмм и комплексных амплитуд.
- •Вращающееся магнитное поле. Принцип работы синхронных и асинхронных двигателей.
- •Электростатическое поле при наличии диэлектриков. Полярные диэлектрики. Зависимость их диэлектрической восприимчивости от температуры.
- •Работа и мощность переменного тока.
- •Основные сведения о сегнетоэлектриках, пьезоэлектриках, пироэлектриках.
- •Пьезоэлектрики
- •Сегнетоэлектрики (сегнетова соль, титанат бария)
- •Объяснение сегнетоэлектрических свойств
- •Резонанс напряжения в цепи переменного тока.
- •I. Сторонние силы.
- •II. Обобщённый закон Ома.
- •Трансформаторы. Векторные диаграммы простейших случаев работы трансформатора.
- •Дифференциальная форма закона Джоуля-Ленца. Работа, совершаемая при прохождении тока, развиваемая мощность.
- •Основные сведения о трехфазном токе. Соединение звездой и треугольником.
- •Токи Фуко. Скин-эффект и его использование в технике.
- •Контактные явления. Законы Вольта. Контактная разность потенциалов.
- •Фильтры низких и высоких частот, основные характеристики и физические принципы их реализации.
- •Выпрямляющее действие полупроводникового контакта Полупроводниковый диод и транзистор
- •Движение заряженных частиц в электрических и магнитных полях.
- •Термоэлектродвижущая сила, эффект Пельтье и эффект Томсона.
- •Ускорители заряженных частиц. Определение удельного заряда электрона и ионов.
- •Механизм электропроводности электролитов. Зависимость их электропроводимости от температуры. Электролиз. Законы Фарадея.
- •Законы Фарадея
- •Электропроводность газов. Основные типы газового разряда. Плазменное состояние вещества.
- •Энергия магнитного поля контуров с током. Энергия магнитного поля при наличии магнетиков.
- •Термоэлектронная эмиссия.
- •Плотность энергии магнитного поля. Индуктивность. Энергия магнетика во внешнем магнитном поле.
- •Закон сохранения энергии для электромагнитного поля.
- •Ток смещения. Система уравнений Максвелла, физический смысл отдельных уравнений. Граничные условия. Материальные уравнения.
- •Объемные силы, действующие на несжимаемые магнетики. Вычисление сил из выражения для энергии.
- •Электромагнитные волны. Волновое уравнение.
- •Диамагнетики. Механизмы намагничивания. Природа диамагнетизма, ларморова прецессия.
- •Плотность потока электромагнитной энергии. Вектор Умова - Пойтинга. Движение электромагнитной энергии вдоль линий передач.
- •Парамагнетики. Механизмы намагничивания. Зависимость парамагнитной восприимчивости от температуры. Закон Кюри.
- •Колебательный контур, свободные незатухающие и затухающие электрические колебания.
- •Колебательный контур, вынужденные электрические колебания.
- •Гиромагнитные эффекты. Соотношение между механическими и магнитными моментами атомов и электронов.
- •Электромагнитные взаимодействия в природе. Электромагнитное поле. Элементарный заряд и его свойства. Закон сохранения заряда.
- •Теорема о циркуляции векторов магнитного поля. Граничные условия для векторов магнитного поля.
- •Индуктивность. Явление самоиндукции. Взаимная индукция. Переходные процессы в цепи с индуктивностью. Взаимная индукция
- •Резонанс токов в цепи переменного тока.
Сегнетоэлектрики (сегнетова соль, титанат бария)
Кристаллы сегнетоэлектриков имеют различную анизотропию свойств и обладают особенностями:
Относительная диэлектрическая проницаемость
 весьма
велика (~ 104)
в некотором температурном диапазоне.
На границе температурного диапазона
сегнетоэлектрик в результате фазового
перехода превращается в поляризованный
диэлектрик.
весьма
велика (~ 104)
в некотором температурном диапазоне.
На границе температурного диапазона
сегнетоэлектрик в результате фазового
перехода превращается в поляризованный
диэлектрик.Рис. 51
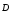 –электрическое смещение нелинейно
зависит от напряженности
–электрическое смещение нелинейно
зависит от напряженности
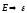 зависит от
зависит от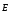 .
.
Значение электрического смещение
 определяется
не только значением напряженности
определяется
не только значением напряженности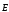 ,
но зависит еще от предшествовавших
состояний поляризации –диэлектрический
гистерезис.
,
но зависит еще от предшествовавших
состояний поляризации –диэлектрический
гистерезис.

Сегнетоэлектрические свойства зависят от температуры. Существует
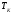 –
температура Кюри – когда сегнетоэлектрик
превращается в результате фазовых
переходов в обычный поляризованный
диэлектрик. У некоторых сегнетоэлектриков
(сегнетова соль) существует две
температуры Кюри (+24 и -18оС)
и сегнетоэлектрические свойства
наблюдаются в температурном интервале.
–
температура Кюри – когда сегнетоэлектрик
превращается в результате фазовых
переходов в обычный поляризованный
диэлектрик. У некоторых сегнетоэлектриков
(сегнетова соль) существует две
температуры Кюри (+24 и -18оС)
и сегнетоэлектрические свойства
наблюдаются в температурном интервале.
Объяснение сегнетоэлектрических свойств
Существует очень сильное взаимодействие между дипольными моментами молекул. Под влиянием этого сегнетоэлектрик подразделяется на отдельные области самопроизвольной (спонтанной) поляризации – диэлектрические домены. Размер доменов определяется минимальной полной энергией системы:
размер домена уменьшается уменьшается суммарная энергия электрического поля доменов
размер домена увеличивается растет поверхностная энергия на границе между соседними доменами.
В обычных условиях спонтанная поляризация не обнаруживается. Домен (~10-6 м) располагаются хаотически т.к. это расположение соответствует минимальной энергии ( в противном случае возникло бы поле, содержащее дополнительную энергию).
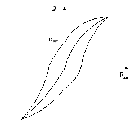
Рис. 52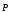 в отдельных областях, перестройка
доменной структуры (Рис. 52).. Происходит
увеличение объема для которых
поляризованность
в отдельных областях, перестройка
доменной структуры (Рис. 52).. Происходит
увеличение объема для которых
поляризованность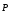 совпадает с
совпадает с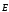 ,
образование новых доменов с направлением
поляризации близким к
,
образование новых доменов с направлением
поляризации близким к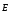 .
.
При высоких
электрических полях
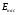 – домены приобретают одинаковую
ориентацию и кристалл становится
монодоменом.
– домены приобретают одинаковую
ориентацию и кристалл становится
монодоменом.
Рис. 53
Применение:
Конденсатор большой емкости при малых размерах с высоким качеством.
Резонанс напряжения в цепи переменного тока.
рассмотренная цепь из последовательно соединенных индуктивности, емкости и активного сопротивления может рассматриваться как колебательная система, так как в ней возможно возникновение электромагнитных колебаний с собственной частотой
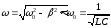 при
при
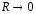 .
.
Эти колебания являются затухающими, так как энергия, сосредоточенная в контуре в момент возникновения колебаний выделяется в виде тепла на активном сопротивлении во время колебательного процесса.
Тогда, при
включении в контур источника переменной
ЭДС, его можно рассматривать как элемент,
инициирующий в контуре вынужденные
колебания с частотой
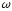 .
Следовательно, уравнение
.
Следовательно, уравнение
 представляет собой
уравнение вынужденных электромагнитных
колебаний под действием внешней
периодически изменяющейся ЭДС.
представляет собой
уравнение вынужденных электромагнитных
колебаний под действием внешней
периодически изменяющейся ЭДС.
Используя физические
величины: собственную частоту
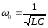 и коэффициент затухания
и коэффициент затухания это уравнение можно представить и в
виде
это уравнение можно представить и в
виде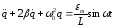 .
.
Как известно, для вынужденных колебаний характерно явление резонанса, которое заключается в возрастании амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к резонансной частоте, зависящей от параметров колебательной системы.
В рассматриваемой цепи - колебательном контуре вынужденные колебания совершают сила тока, заряд и напряжение на конденсаторе, а также напряжение на катушке индуктивности.
Резонансными кривыми называются зависимости амплитудных значений, совершающих вынужденные колебания физических величин, от частоты внешнего воздействия, т.е., в нашем случае, от частоты источника ЭДС.
Закон Ома для
рассматриваемой цепи – колебательного
контура позволяет проанализировать
зависимость амплитуды силы тока от
частоты источника ЭДС:
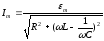 .
.
Если амплитудное значение ЭДС, а также величины активного сопротивления, емкости и индуктивности постоянны, то амплитудное значение силы тока зависит только от частоты.
Максимальная
амплитуда силы тока:
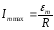 при
при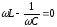 .
В этом случае частота источника ЭДС
совпадает с собственной частотой
колебательного контура:
.
В этом случае частота источника ЭДС
совпадает с собственной частотой
колебательного контура: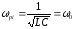 ,
,
т.е. для вынужденных колебаний силы тока наблюдается резонанс.
Резонансная частота для заряда и напряжения всегда меньше, чем резонансная частота для тока, а резонанс выражен тем больше, чем меньше активное сопротивление контура.
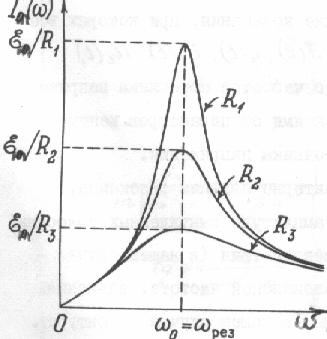
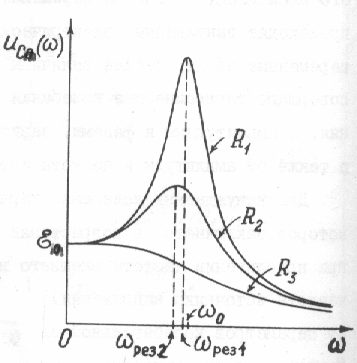
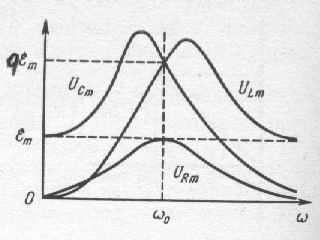
РИС.155 РИС.156 РИС.157 РИС.158
Максимальное значение напряжения на катушке индуктивности (см.§ 51) преобразуем также, используя понятия собственной частоты и коэффициента затухания:
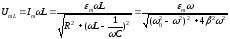 .
Резонансную частоту можно найти, взяв
производную по частоте от этого выражения
и приравняв ее к нулю. Резонансная
частота для напряжения на катушке
индуктивности равна:
.
Резонансную частоту можно найти, взяв
производную по частоте от этого выражения
и приравняв ее к нулю. Резонансная
частота для напряжения на катушке
индуктивности равна:
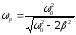 .
.
Если преобразовать
и сравнить выражения для резонансных
частот на конденсаторе и на катушке
индуктивности с резонансной частотой
тока:
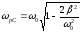 ,
, ,
,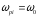 ,
то можно сделать вывод, что , общем
случае, резонансная частота для напряжения
на конденсаторе всегда меньше, а для
напряжения на катушке индуктивности
всегда больше, чем резонансная частота
для силы тока (и напряжения на активном
сопротивлении). Резонансные кривые
для напряжений на активном сопротивлении,
катушке индуктивности и емкости показаны
на рис.158.
,
то можно сделать вывод, что , общем
случае, резонансная частота для напряжения
на конденсаторе всегда меньше, а для
напряжения на катушке индуктивности
всегда больше, чем резонансная частота
для силы тока (и напряжения на активном
сопротивлении). Резонансные кривые
для напряжений на активном сопротивлении,
катушке индуктивности и емкости показаны
на рис.158.
Для представляющих
практический интерес контуров с малым
затуханием,
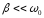 ,
членом
,
членом можно
пренебречь. В этом случае резонанс для
всех переменных электрических величин:
силы тока, заряда и напряжения на
конденсаторе, напряжения на катушке
индуктивности наступает практически
одновременно при частоте источника,
равной частоте свободных колебаний в
контуре:
можно
пренебречь. В этом случае резонанс для
всех переменных электрических величин:
силы тока, заряда и напряжения на
конденсаторе, напряжения на катушке
индуктивности наступает практически
одновременно при частоте источника,
равной частоте свободных колебаний в
контуре:
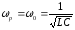 .
При резонансе сдвиг фаз между током и
напряжением равен нулю (рис.159).
.
При резонансе сдвиг фаз между током и
напряжением равен нулю (рис.159).
Следовательно, добротность – величина обратная относительной ширине пропускания или относительной ширине резонансной кривой.
Резонанс используется для выделения из сложного «сигнала» (зарегистрированного напряжения) нужной составляющей. Это имеет практическое значение в радиотехнике при приеме и настойке на определенную частоту радиосигнала. Чем выше добротность контура, тем уже резонансная кривая и тем легче «отстраиваться» от передач, ведущихся на соседних частотах.
На практике добротность контура подбирается и с учетов необходимого качества приема сигнала, так как с уменьшение ширины резонансной кривой уменьшается информация (диапазон частот) «пропускаемый» контуром.
Электрическое поле при наличии постоянного тока. Уравнение непрерывности. Обобщенный закон Ома. Сторонние электродвижущие силы.
Характеристики тока.
Электрический ток — упорядоченное движение электрических зарядов.
Заряды — носители тока:
в металлах и полупроводниках - электроны;
в электролитах и газах – положительный и отрицательный ионы.
При отсутствии электрического поля носители тока совершают хаотическое (тепловое) движение и через любую поверхность S проходит в обе стороны в среднем одинаковое количество носителей одного знака (IS = 0 — ток через поверхность S).
При включении поля на хаотическое движение носителей накладывается упорядоченное движение с некоторой средней скоростью υ (средняя дрейфовая или упорядоченная скорость).
Количественными характеристиками тока служат сила тока I и плотность тока j.
Так как электрический ток может быть распределён неравномерно по поверхности => вводим характеристику плотности тока j.
Модуль этого вектора │j│ численно равен отношению силы тока dI через элементарную площадку, перпендикулярную направлению движения носителей. За направление j принимают направление вектора скорости упорядоченного движения υ положительных носителей (Рис. 74).
I
=
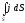 =
=
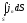
=>
jn = dI/dS
Зная
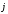 (
(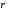 )=> найти I
через
поверхность
S.
)=> найти I
через
поверхность
S.
УРАВНЕНИЕ НЕПРЕРЫВНОСТИ.
Электрический ток является стационарным лишь при определенных условиях. Выясним эти условия.
Если ток нестационарный, т.е. I=f(t), то через замкнутую неподвижную поверхность, ограничивающую произвольный объем, может входить и выходить различное количество зарядов.
Тогда объемная
плотность зарядов в этом объеме:

Сила тока,
определяется зарядом, проходящим через
поверхность в единицу времени :
 .
По закону сохранения заряда, скорость
изменения количества заряда внутри
объема и заряд, вышедший через поверхность
в единицу времени, в сумме должны
равняться нулю:
.
По закону сохранения заряда, скорость
изменения количества заряда внутри
объема и заряд, вышедший через поверхность
в единицу времени, в сумме должны
равняться нулю: или
или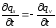 .
Используем, что :
.
Используем, что :
 и
и
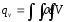 .
Тогда:
.
Тогда: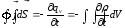 - уравнение непрерывности в интегральной
форме или закон сохранения заряда при
наличии тока.
- уравнение непрерывности в интегральной
форме или закон сохранения заряда при
наличии тока.
Физический
смысл этого уравнения в том, что убыль
заряда в единицу времени внутри замкнутой
поверхности равна потоку вектора
плотности тока через данную поверхность.
 - уравнение непрерывности в дифференциальной
форме. Если ток стационарный, то
распределение зарядов в пространстве
неизменно, т.е.
- уравнение непрерывности в дифференциальной
форме. Если ток стационарный, то
распределение зарядов в пространстве
неизменно, т.е.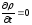
Тогда:
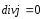 или
или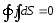 - условие стационарности тока в
дифференциальном и интегральном виде.
- условие стационарности тока в
дифференциальном и интегральном виде.
Обобщённый закон Ома.
