- •Оглавление
- •Закон Кулона. Экспериментальные проверки закона Кулона. Теорема Остроградского-Гаусса. Дифференциальная формулировка закона Кулона.
- •Классическая теория электропроводности и ее затруднения. Объяснение законов Ома, Джоуля-Ленца, Видемана-Франца на основе классической электронной теории.
- •Объяснение закона Джоуля-Ленца с точки зрения классической электронной теории
- •Закон взаимодействия элементов тока (закон Лапласа-Био-Савара-Ампера). Полевая трактовка закона взаимодействия элементов тока. Релятивистская природа магнитного поля.
- •Нахождение электрического поля с использованием потенциала, прямым применением закона Кулона и с использованием теоремы Гаусса.
- •Закон Био-Савара. Вектор магнитной индукции. Закон Ампера.
- •Закон Ампера
- •Зависимость электропроводимости от температуры, явление сверхпроводимости.
- •Емкость уединенного проводника. Система проводников. Конденсаторы и их емкость. Общая задача электростатики. Понятие о методе изображений для решения некоторых электростатических задач.
- •Теорема о циркуляции вектора магнитной индукции в стационарном случае. Вихревой характер магнитного поля.
- •Электростатическое поле при наличии диэлектриков. Поляризация. Связанные и свободные заряды. Электростатическая теорема Гаусса при наличии диэлектриков.
- •Понятие о зонной теории твердых тел. Расщепление энергетических уровней и образование зон. Энергетические зоны металлов, полупроводников и изоляторов.
- •Электрическое смещение и диэлектрическая проницаемость. Преломление силовых линий на границе раздела диэлектриков.
- •Собственная проводимость полупроводников. Примесная (электронная и дырочная) проводимость. Доноры и акцепторы. Температурная зависимость проводимости полупроводников.
- •Энергия электростатического поля. Энергия взаимодействия при непрерывном распределении зарядов. Собственная энергия.
- •Индукции токов в движущихся проводниках. Закон электромагнитной индукции Фарадея.
- •Объемная плотность энергии электрического поля. Энергия поля поверхностных зарядов. Энергия заряженных проводников.
- •Энергия заряженных проводников
- •Цепи квазистационарного переменного тока. Цепь с источником переменных сторонних эдс, сопротивлением, емкостью, и индуктивностью.
- •Силы в электрическом поле. Силы, действующие на точечный заряд, диполь и непрерывно распределенный заряд. Силы, действующие на диэлектрик и проводник. Энергетический метод определения сил.
- •Закон электромагнитной индукции Фарадея. Дифференциальная формулировка закона электромагнитом индукции Фарадея.
- •Энергия диполя во внешнем поле.Поле диполя
- •Метод векторных диаграмм и комплексных амплитуд.
- •Вращающееся магнитное поле. Принцип работы синхронных и асинхронных двигателей.
- •Электростатическое поле при наличии диэлектриков. Полярные диэлектрики. Зависимость их диэлектрической восприимчивости от температуры.
- •Работа и мощность переменного тока.
- •Основные сведения о сегнетоэлектриках, пьезоэлектриках, пироэлектриках.
- •Пьезоэлектрики
- •Сегнетоэлектрики (сегнетова соль, титанат бария)
- •Объяснение сегнетоэлектрических свойств
- •Резонанс напряжения в цепи переменного тока.
- •I. Сторонние силы.
- •II. Обобщённый закон Ома.
- •Трансформаторы. Векторные диаграммы простейших случаев работы трансформатора.
- •Дифференциальная форма закона Джоуля-Ленца. Работа, совершаемая при прохождении тока, развиваемая мощность.
- •Основные сведения о трехфазном токе. Соединение звездой и треугольником.
- •Токи Фуко. Скин-эффект и его использование в технике.
- •Контактные явления. Законы Вольта. Контактная разность потенциалов.
- •Фильтры низких и высоких частот, основные характеристики и физические принципы их реализации.
- •Выпрямляющее действие полупроводникового контакта Полупроводниковый диод и транзистор
- •Движение заряженных частиц в электрических и магнитных полях.
- •Термоэлектродвижущая сила, эффект Пельтье и эффект Томсона.
- •Ускорители заряженных частиц. Определение удельного заряда электрона и ионов.
- •Механизм электропроводности электролитов. Зависимость их электропроводимости от температуры. Электролиз. Законы Фарадея.
- •Законы Фарадея
- •Электропроводность газов. Основные типы газового разряда. Плазменное состояние вещества.
- •Энергия магнитного поля контуров с током. Энергия магнитного поля при наличии магнетиков.
- •Термоэлектронная эмиссия.
- •Плотность энергии магнитного поля. Индуктивность. Энергия магнетика во внешнем магнитном поле.
- •Закон сохранения энергии для электромагнитного поля.
- •Ток смещения. Система уравнений Максвелла, физический смысл отдельных уравнений. Граничные условия. Материальные уравнения.
- •Объемные силы, действующие на несжимаемые магнетики. Вычисление сил из выражения для энергии.
- •Электромагнитные волны. Волновое уравнение.
- •Диамагнетики. Механизмы намагничивания. Природа диамагнетизма, ларморова прецессия.
- •Плотность потока электромагнитной энергии. Вектор Умова - Пойтинга. Движение электромагнитной энергии вдоль линий передач.
- •Парамагнетики. Механизмы намагничивания. Зависимость парамагнитной восприимчивости от температуры. Закон Кюри.
- •Колебательный контур, свободные незатухающие и затухающие электрические колебания.
- •Колебательный контур, вынужденные электрические колебания.
- •Гиромагнитные эффекты. Соотношение между механическими и магнитными моментами атомов и электронов.
- •Электромагнитные взаимодействия в природе. Электромагнитное поле. Элементарный заряд и его свойства. Закон сохранения заряда.
- •Теорема о циркуляции векторов магнитного поля. Граничные условия для векторов магнитного поля.
- •Индуктивность. Явление самоиндукции. Взаимная индукция. Переходные процессы в цепи с индуктивностью. Взаимная индукция
- •Резонанс токов в цепи переменного тока.
Нахождение электрического поля с использованием потенциала, прямым применением закона Кулона и с использованием теоремы Гаусса.
с использованием теоремы Гаусса.
Положения: При использовании теоремы Гаусса для расчета электрических полей нужно учитывать, что:
1) рассчитать можно только поле, которое обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической).
2)
симметрия и конфигурация поля должны
быть такими, чтобы можно было найти
достаточно простую замкнутую поверхность
S
(называемую гауссовой
поверхностью), такую, чтобы отдельные
ее части Si
были параллельны
вектору
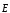 (тогда
(тогда
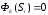 )
илиотдельные
ее части Sj
были перпендикулярны
)
илиотдельные
ее части Sj
были перпендикулярны
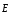 и напряженность на них была постоянна
по модулю (тогда
и напряженность на них была постоянна
по модулю (тогда
 ).
).
Если этого нет, задачу о нахождении поля приходится решать помощью метода непосредственного интегрирования или с помощью других методов, с которыми мы ознакомимся ниже.
Рассчитаем:
поле бесконечной заряж. равном. плоскости
Дано:
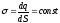
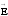 - ?
- ?
Из симметрии задачи
вектор
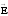
плоскости и в симметр. отн. плоскости
точках одинаков. по модулю и противоп.
по направлению (Рис.
11
). Гауссова
поверхность – цилиндр. Тогда поток
вектора напр. находится как сумма потоков
через основания и боковую поверхность.
плоскости и в симметр. отн. плоскости
точках одинаков. по модулю и противоп.
по направлению (Рис.
11
). Гауссова
поверхность – цилиндр. Тогда поток
вектора напр. находится как сумма потоков
через основания и боковую поверхность.
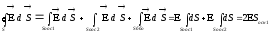
теор. Г.
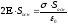
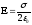 напр.
равном. заряж. плоскости
напр.
равном. заряж. плоскости
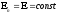
Выражения для напряженности полей заряженных тел (в вакууме), обладающих специальной симметрией, рассчитанных по теореме Гаусса.
|
Равномерно заряженная с линейной плотностью λ бесконечная нить (поле цилиндрической симметрии) |
(r — расстояние от нити по перпендикуляру к ней) |
|
Равномерно заряженная зарядом q по поверхности сфера радиусом R (поле сферической симметрии) |
(r — расстояние от центра сферы) |
|
Заряд равномерно распределен с объемной плотностью ρ по объему шара радиуса R (поле сферической симметрии) |
(r — расстояние от центра шара) |
прямым применением закона Кулона
Напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждый из зарядов в отдельности:
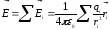 , (6)
, (6)
где ri — расстояние между зарядом qi и интересующей нас точкой поля.
Это утверждение называют принципом суперпозиции (наложения) электрических полей. Поле точечного заряда является фундаментальным, потому что, используя формулу поля точечного заряда и принцип суперпозиции, можно расчитать поле любого (!) заряда.
Распределение зарядов. Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру (электроны, ядра), и считать, что они «размазаны» определенным образом и пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. Это позволяет значительно упрощать расчеты, не внося сколько-нибудь значительной ошибки.
При переходе к непрерывному распределению вводят понятие о плотности зарядов — объемной ρ, поверхностной σ и линейной λ. По определению,
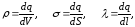 (7)
(7)
где dq — заряд, заключенный соответственно в объеме dV, на поверхности dS и на длине dl.
C учетом этих распределений формула (6) может быть представлена в другой форме. Например, если заряд распределен по объему, то надо заменить qi на dq = ρ dV и ∑ на ∫, тогда
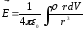 ,
(8)
,
(8)
где интегрирование проводится по всему пространству, в котором ρ отлично от нуля (Рис.5).
V
dV
A
dq
q
Рис.
5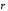
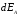
Таким образом,
зная распределение зарядов, мы можем
полностью решить задачу о нахождении
напряженности электрического поля по
формуле (6), если распределение дискретно,
или по формуле (8), если распределение
непрерывно. Этот метод нахождения
электрического поля получил название
метод
непосредственного интегрирования.
В общем случае расчет сопряжен со
значительными трудностями (правда, не
принципиального характера). Действительно,
для нахождения вектора
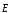 надо вычислить сначала его проекцииЕx
, Еy
, Еz
, а это по
существу, три интеграла типа (8).
надо вычислить сначала его проекцииЕx
, Еy
, Еz
, а это по
существу, три интеграла типа (8).
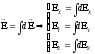 метод
непосредственного интегрирования
метод
непосредственного интегрирования
Пример 1.1 Заряд q > 0 равномерно распределен по тонкому кольцу радиусом R. Найти напряженность Е электрического поля на оси кольца как функцию расстояния z от его центра.
Решение.
Легко сообразить, что в данном случае
вектор Е должен быть направлен по оси
кольца (рис. 2). Выделим на кольце элемент
dl.
Запишем выражение для составляющей
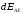 от этого элемента в точке А:
от этого элемента в точке А:

где λ = q/2πR. Для всех элементов кольца r и R будут одними и теми же, поэтому интегрирование этого выражения сводится просто к замене dl на q.
dl
r
R
0 α
Рис.2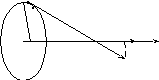
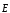 x
x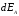
В результате получаем:
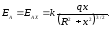
Видно, что при x » а поле Е = q/4πε0x2 , т. е. на больших расстояниях эта система ведет себя как точечный заряд.
с использованием потенциала
находим потннциал. Связь потенциала и напряженности:
E = -∆φ