Закон магнитного взаимодействия токов. Сила лоренца.

Мы уже говорили, что проводники с током создают вокруг себя магнитное поле и т.о. действуют на находящиеся около них постоянные магниты. В свою очередь, магнитное поле (МП) действует на проводник с током. Действие МП на проводники с током было обнаружено Эрстедом и Ампером. Ампер подробно исследовал это явление и пришел к выводу, что сила F, которая действует на прямолинейный проводник с током, находя­щийся в однородном МП, пропорциональна силе тока I в проводнике, его длине l, маг­нитной индукции`В и sina, между направлением тока в проводнике и вектором `В:

F = kIBlsina - закон Ампера. (1)

В векторной форме:

`F = kI [`lх`В].

Закон Ампера (1) легко обобщить на случай неоднородного МП и проводника произ­вольной формы. В самом деле, бесконечно малый элемент dl проводника любой формы можно считать прямолинейным, а МП в области, занятой элементом dl, можно считать однородным.

Поэтому в общем случае закон Ампера

dF = kIB dl sina (2)

где dF - сила, действующая на dl, k -зависит только от выбора единиц величин I, В, l и F. Если все в СИ, то k = 1. Направление d`F определяется по правилу левой руки: `В- вхо­дит в ладонь, а пальцы - направление I.

Закон Ампера позволяет определить числовое значение магнитной индукции В. Если a=90°, то sina= 1, и

В = dF/I dl, (3)

т.е. магнитная индукции В численно равна силе, действующей со стороны поля на едини­цу длины проводника, по которому течет электрический ток единичной силы и который расположен перпендикулярно направлению магнитного поля. Т.О., магнитная индукция является сило­вой характеристикой МП, подобно тому, как напряженность Е является силовой характери­стикой электростатического поля.

Единицей магнитной индукции является тесла (Т) - магнитная индукция такого однородного МП, которое действует с силой 1Н на каждый метр длины прямолинейного проводника с током в 1 А, расположенного перпендикулярно направ­лению поля.

1Т = 1Н/А×м = 1Дж/А×м² = 1В×с/м².

Если магнитное поле индукции `В создается другим проводником с током такого же направления как и в первом, и проводники параллельны, то два параллельных тока одинакового направления притягиваются друг к другу с силой

dF = (mm₀/4p)2I₁I₂ dl/R. (4)

Если токи имеют противоположные направления, то используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (4).

Поскольку всякий ток есть движение заряженных частиц (электронов или ионов), от­сюда следует, что на движущийся заряд в магнитном поле действует сила:

`F<sub>л</sub> = q[`U´`B] - сила Лоренца.

Сила Лоренца численно равна

F_л =|q|U sina,

где a - угол между скоростью движущейся частицы `U и вектором магнитной индукции`В.

Сила Лоренца всегда направлена перпендикулярно скорости заряженной частицы, сообщая ей нормальное ускорение. Следовательно, сила Лоренца не совершает работы. Она изменяет только направление скорости движения частицы в магнитном поле. Абсо­лютное значение скорости заряда и его кинетическая энергия при движении в магнитном поле не изменяются.

В общем случае на движущийся заряд помимо МП с индукцией `В может еще дей­ствовать и электрическое поле с напряженностью `Е, Тогда результирующая сила `F, приложенная к заряду, равна геометрической сумме силы F_е =q Е, действующей на заряд со стороны электрического поля, и силы Лоренца:

`F =q`E +q[`U´`B] -формулa Лоренца.

. . . . . . . . .

. . . . . . . . .

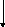. +q. . . . . `U

. . . . . . . . .

`F

Рис.6. Поле `B направлено к читателю.

Движение заряженных частиц в электрическом и магнитном полях.

Полученное выше выражение для силы Лоренца позволяет установить ряд закономерностей движения заряженных частиц в магнитном поле, лежащих в основе устройства электронного микроскопа, масс-спектрографа и ускорителей заряженных частиц.

Рассмотрим движение заряженных частиц в однородном МП. При этом будем считать, что на частицы не действуют никакие электрические поля.

Начнем с простейшего случая - движения заряженной частицы вдоль линий индукции МП. При этом угол a между `U и `В равен 0 или p, поэтому F_л = 0, т.е. МП не действует на частицу. Она будет двигаться по инерции - равномерно и прямолинейно.

Пусть частица, имеющая заряд q, движется перпендикулярно линиям магнитной индукции (a=p/2). Тогда

F_л = |q|UВ. (3)

Следовательно, частица движется в плоскости, перпендикулярной вектору`В, причем сила Лоренца является центробежной силой, вычисляемой по формуле

F_л = mU²/r , (4)

где m -масса частицы, r- радиус кривизны ее траектории. Приравняв (3) и (4), найдем

r = |m/q|U/В,

т.к. в однородном МП `В=соnst, а числовое значение скорости частицы не изменяется, то pадиус кривизны траектории частицы оказывается постоянным. Поэтому она будет двигаться по окружности плоскость которой ^`В, а радиус пропорционален отношению скорости частицы к произведению ее удельного заряда q/т на индукцию `В поля.

Поскольку направление силы`F_л и вызываемого ею отклонения заряженной частицы в МП зависят от знака ее заряда q, то если частица движется в плоскости чертежа слева направо, а МП направлено из-за чертежа его плоскости, то при q >0 частица отклонится вниз, а при q<0 - вверх. Т.о., по характеру отклонения частицы в МП можно судить о знаке ее заряда. Этим широко пользуются в исследованиях элементарных частиц. На этом принципе работают приборы масс-спектрометры, используемые для изучения химического состава различных проб (в том числе и геологических).

Частица движется по окружности радиуса г равномерно. Поэтому период обращения частицы

Т = 2pr/U = 2p | m/q | /В - период не зависит от скорости частицы.

Общий случай движения заряженной частицы в магнитном поле дает винтовую линию.