2. Линии напряженности. Поток вектора на­пряжённости электрического поля.

Для того, чтобы описать электрическое поле, нужно задать Е в каждой точке поля . Это можно сделать аналитически, выражая зависимость Е(х,у,z) в виде формул. Однако, это можно сделать и графически с помощью так называемых линий напряженности или силовых линий.

Силовой линией, или линией вектора напряженности поля, называют ли­нию, проведенную в электрическом поле, для которой направление каса­тельной в любой точке совпадает с направлением вектора напряженности поля (рис.2)

`E

Рис.2 `E

Т.к. касательная определяет два взаимно противоположных направления, то силовой линии приписывают определенное направление, отмечая его на чертеже стрелкой.

Густота силовых линий на чертеже отражает величину напряжен­ности поля, а именно, число силовых линий, проходящих через единицу поверхности, перпендикулярной к силовым линиям, равно ( или пропор­ционально) величине напряженности поля в данном месте. Вследствие на­глядности графический способ представления полей широко применяют в электротехнике.

Из сказанного следует, что силовую линию можно провести через всякую точку поля. Далее, т.к. в каждой точке поля вектор напряженности имеет вполне определенное (одно!) положение, то силовые линии нигде не пересекаются.

В качестве примера рассмотрим картину силовых линий точечного заряда. Для точечного заряда `E||`r и линии напряженности направлены по радиусам, проведённым из заряда. Для положительного заряда (q>0) эти линии исходят из заряда и уходят в ¥ (рис.3 а). Для отрицательного заряда (q<0) `E направлен против радиус-вектора `r, а линии напряженности идут из ¥ и сходятся в точке нахождения заряда (рис.3 б). Как видно из рисунка, густота линий убывает обратно пропорционально квадрату расстояния от заряда, т.е. так же, как и

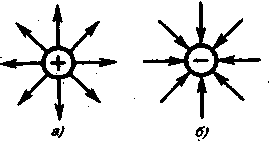
Рис.3.

напряженность поля.

Т.е. густота линий равна отношению полного числа линий N к ве­личине поверхности сферы радиуса r, т.е. N/4pr²~1/r².

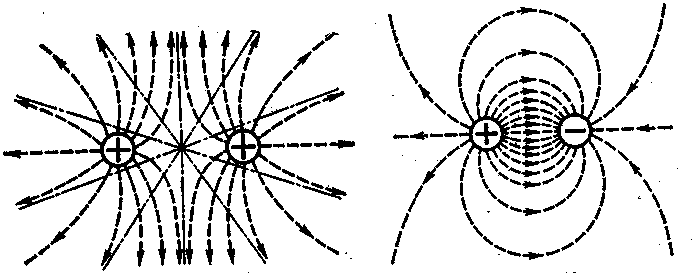
На рис.4 показано электрическое поле между двумя равными по величине точечными зарядами одинаковых и противоположных (рис.5) знаков, расположенными на рас­стоянии l друг от друга (диполь).

Рис.4. Рис.5. (Дипольный момент Р = q l ).

Связь между электрическим полем и его источником может быть выражена до­статочно просто. Для этого введём понятие потока вектора на­пряженности, которое используется при формулировке важнейших свойств электрического, магнитного и других векторных полей.

Рассмотрим в пространстве некоторое электрическое поле и замкнутую поверх­ность произвольной формы.

Разделим всю поверхность на столь малые части, что поверхность каждой части (элемента поверхности) мож­но считать практически плоской; на такой поверхности вектор напряженности электрического поля не будет заметно меняться. Направление элемента поверхности представим вектором нормали. За положительную нормаль к поверхности примем внешнюю нормаль, т.е. нормаль, направленную на­ружу. Способ разделения поверхности на элементы не имеет значения, пока элементы достаточно малы. Число силовых линий, равных скалярному произведению

N = (`E×`n)dS_i = Ф_i - называется потоком вектора напряженности через элемент поверхности dS_i.

Величина Ф может быть >0 и<0, т.к. нормаль может быть как поло­жительной, так и отрицательной.

Теперь сложим потоки через все элементы поверхности и получим поток через всю поверхность

Ф = ò (`E×`n)dS =ò (E_n ×dS,

где Е_n - проекция `Е на направление нормали к площадке dS, где интеграл берется по поверхности S.

Пусть Вас не пугает сложность вычисления таких интегралов для поверхностей сложной формы. Удивительное свойство, которое мы с вами сейчас рассмотрим, делает такие вычисления ненужными!

Теорема Остроградского-Гаусса.

1). Возьмём наиболее простой случай: предположим, что поле созда­но изолированным положительным точечным зарядом q и что поверх­ностью является сфера радиуса r, в центре которой расположен точечный заряд (Риc. 6). Чему равен поток Ф через такую поверхность?

Рис.6.

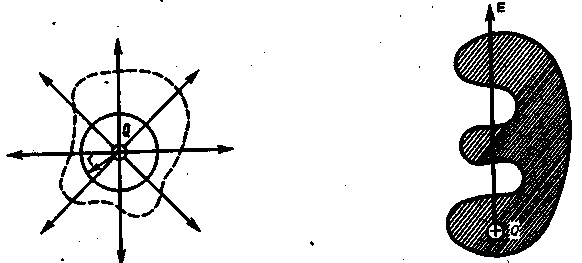
Ответить на этот вопрос легко, т.к. в каждой точке поверхности

`E = (1/4pe<sub>0</sub>)(q/r<sup>3</sup>)`r,

а поверхность сферы S=4pr², тогда

Ф = E×4pr²= (q/4pe₀ r²) 4pr²=q/e₀.

Как мы видим из этой формулы, поток не зависит от размеров сфе­ры.

2). Покажем теперь, что поток не зависит и от формы поверхности, окружающей заряд q. Проведем две концентрические сферы разных радиусов. Мы увидим, что число линий напряженности электрического поля, пронизывающих сферы, одинаково. Между этими сферами линии вектора напряженности `Е идут непрерывно, нигде не заканчиваясь и не начинаясь вновь. Поэтому, если мы проведем между этими сферами замкнутую поверхность S₁ произвольной формы, тоже охватывающую заряд q, то поток вектора напряженности через эту поверхность также будет равен q/e₀.

Напомню, что линии напряженности электрического поля начинаются и заканчиваются только на электрических зарядах. Если замкнутая поверх­ность не охватывает заряда, то поток вектора электрического поля через эту поверхность равен нулю, т.к. число силовых линий, входящих в поверхность, рав­но числу выходящих из неё.

3). Пусть поле создается не одним точечным зарядом, а произволь­ной системой точечных зарядов q₁, q₂, q_3…q_n. По принципу суперпозиции на­пряжённость результирующего электростатического поля равна векторной сумме напряжённостей электростатических полей, создаваемых каждым из зарядов в отдельности :

`E = `E₁+`E<sub>2</sub> +`E₃ +…+`E<sub>n</sub> = S`E_i.

поэтому проекция вектора `Е на на­правление нормали к площади dS равна алгебраической сумме проекций всех векторов `Е_i на это направление

Поток напряженности результирующего поля сквозь произвольную замкнутую поверхность S, охватывающую заряды q₁, q₂, …q_k , и не охватывающую заряды q_k+1…q_m, равен , но Ф_i=0, если i>k

поэтому

,т.е.

поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов, охватываемых этой поверхностью, к электрической постоянной. Это и есть теорема Оетроградского -Гаусса применительно к электростатическому полю в вакууме.

Теорема Остроградского-Гаусса выведена нами как прямое следствие из закона Кулона. Она позволяет сравнительно просто рассчитывать электрические поля при симмет­ричных распределениях зарядов и окружающих их диэлектриков.

Для характеристики электрического поля наряду с `Е удобно ввести ещё одну векторную ве­личину `D , называемую электрическим смещением или электрической индукцией. Для поля в электрически изотропной среде связь `D и `E в СИ имеет вид

`D = ee<sub>0</sub> `E

Тогда _к

-теорема Остроградского-Гаусса.

Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью.

Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Остроградского-Гаусса.

Пример 1. Равномерно-заряженная плоскость.

Имеется безграничная плоскость, заряженная равномерно с поверхностной плот­ностью заряда s. Найти напряженность Е(х), где х - расстояние до плоскости.

Из симметрии задачи очевидно, что линии напряженности должны быть направлены симметрично в обе стороны от плоскости ^ ей. В этом случае в качестве замкнутой поверхности в теореме Остроградского-Гаусса удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограниченный двумя плоскими основаниями, перпендикулярными к силовым линиям и расположенными по обе стороны заряженной плоскости (рис.7).

Рис. 7. Рис.8.

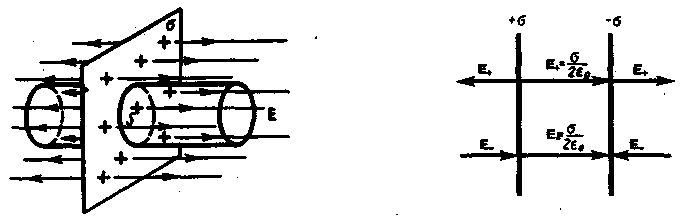
Т.к. образующие цилиндра параллельны вектору напряженности электрического поля `Е, то поток через боковую поверхность цилиндра равен нулю и поэтому полный по­ток сквозь цилиндр равен сумме потоков через его основания

Ф =^:2ЕS.

Полный заряд, заключенный внутри цилиндра равен Ss. Поэтому применяя теорему О-Г, имеем:

2ЕS =sS/e₀, откуда

Е = s/2e₀,

т.е. `Е не есть функция расстояния. Следовательно `Е = соnst по величине и по направлению.

Если плотность заряда отрицательная, т.е. (-s), то линии напряжённости имеют противоположное направление.

Пример2. Определим поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноимёнными зарядами (плоский конденсатор, рис.8). Считаем плоскости бесконечными.

Заряженная плоскость каждой пластины создаст по обе стороны от себя напря­женность поля, выражаемую формулой ±s/2e₀. Внутри металлических пластин и вне конденсатора эти поля направлены противоположно и поэтому в сумме дают нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и, складываясь, дают у поверхности пластин напряженность Е = s/e₀. В данном частном случае электрическое поле од­нородно и поэтому его напряженность у поверхности пластин такая же, как и в других точках поля.

Пример 3. Равномерно заряженный шар.

Рассмотрим электрическое поле между двумя шаровыми концентрическими электродами (рис.9) - шаровой конденсатор. Под действием взаимного притяжения (-) и (+ ) заря­ды расположатся только на поверхности внутреннего шара и на внутренней поверх­ности внешнего

Рис.9. Рис.10.

электрода. Из условий симметрии очевидно, что заряды на обоих ша­ровых электродах будут распределены равномерно, и что линии напряженности электрического поля могут быть только радиальными прямыми. Выберем в качестве замкнутой поверхности сферу с ра­диусом r, расположенную между электродами и имеющую общий центр с обоими элек­тродами.

По теореме Остроградского-Гаусса

Ф = Е(r)4pr² = q/e₀,

откуда

Е(r)=q/4pe₀r². (*)

Эта формула показывает, что напряжённость поля между электродами за­висит от расстояния r рассматриваемой точки поля от центра внутреннего шара, но не зависит вовсе от размеров внешнего электрода. Ту же напряженность поля получим, если радиус внешнего электрода будет как угодно велик. Роль внешнего электрода могут играть различные удалённые заземлённые предметы, например стены, пол и потолок комна­ты. Поэтому часто говорят просто о поле заряженного шара (рис.10), не указывая, что именно является вторым электродом. Из формулы (*) следует, что электрическое поле шара, равномерно заряженного по поверхности, во внешнем про­странстве совпадает с полем точечного заряда, равного полному заряду шара и помещённого в центре шара. Если бы мы рассмотрели шар, заряженный равномерно по объёму, то напряженность поля тоже выражалась бы формулой (*). Напряженность же поля внутри шара в обоих случаях различна. В случае шара, равномерно заряженного по поверхности Е = О в любой внутренней точке. Если же шар заряжен равномерно по объёму, то Е= 0 только в центре шара и с увеличением расстояния r от центра воз­растает пропорционально r. В справедливости этого можно убедиться также при помощи теоремы Остроградского-Гаусса.

Пример: «клетка Фарадея».

металл

++++++++++++++++

`Е = 0

+ +

+ +

+ +

+ +

+ + + + + + + + + + + + + + +

Рис.11.