
- •Определение земного ускорения свободного падения при помощи оборотного и математического маятников.
- •Результаты измерений и расчётов ускорения свободного падения с помощью математического маятника.
- •Сложение гармонических колебаний
- •1. Биения.
- •Порядок выполнения задания.
- •1.Изучить биения.
- •2.Изучить сложение взаимно перпендикулярных колебаний.
- •Лабораторная работа № 5. Деформации сдвига и кручения.
- •Элементы теории.
- •Порядок выполнения задания.
- •Контрольные вопросы:
- •Литература:
- •Измерение температуры электрическими контактными термометрами.
- •Температурные шкалы и единицы измерения.
- •Электрические контактные термометры
- •1. Металлические термометры сопротивления.
- •2. Полупроводниковые термометры сопротивления.
- •3. Термоэлектрические термометры.
- •Порядок выполнения задания.
- •Порядок выполнения работы
- •Лабораторная работа№7
- •Лабораторная работа № 9. Изучение методов измерения оптических показателей преломления твердых тел.
- •Контрольные вопросы:
- •Литература.
- •Лабораторная работа№10
- •Тогда из (1) получаем
- •Таким образом, задерживающее напряжение Uз линейно зависит от частоты падающего на фотоэлемент излучения.
- •1. Собрать схему с сопротивлением r (рис.1). Переключатели пределов шкалы вольтметра и амперметра установить на максимальные значения.
- •Лабораторная работа № 12. Поглощение света в жидких и твердых веществах.
- •Контрольные вопросы:
- •Литература:
- •Лабораторная работа № 13 определение показателя преломления жидкостей с помощью рефрактометра.
- •3.Порядок работы.
- •Контрольные вопросы.
- •Литература.
- •Лабораторная работа № 14. Определение концентраций водных растворов сахара по вращению плоскости поляризации.
- •Литература.
- •Лабораторная работа № 15.
- •При вычислении введем вспомогательную переменную
- •Отсюда постоянная Стефана-Больцмана
- •Вопросы.
- •С учетом этого замечания соотношение (2) следует записать в виде
- •Контрольные вопросы.
- •Литература.
1. Биения.
Рассмотрим сложение двух гармонических колебаний, происходящих вдоль одной прямой с частотами ω1 и ω2, незначительно отличающихся друг от друга. (Ω=( |ω1 - ω2 |<< ω1 и Ω<< ω2 ).Пусть в начальный момент времени фазы складываемых колебаний одинаковы. Тогда эти колебания запишутся в виде
![]() и
и![]() (4)
(4)
Найдем
сумму двух таких колебаний, предположив
для простоты сначала, что их амплитуды
одинаковы (A1
= A2):
![]() (5)
(5)

Рис. 3.
Отсюда
видно, что результирующее колебание
(биение) происходит с частотой (ω1+ω2)/2,
а амплитуда колебаний со временем
изменяется в пределах от 2A1
до 0 по закону
![]() (рис. 3). Значение 2A1
достигается тогда, когда фазы складываемых
колебаний совпадают, а нуль - когда фазы
противоположны. Периодическое изменение
результирующей амплитуды, получающееся
при сложении колебаний, совершающихся
с близкими частотами и вдоль одной
прямой, называют биениями. Циклическая
частота биений Ω=
|ω1
-
ω2
|,
период биений Т
= 2π/
Ω (рис.3) и
частота биений
(рис. 3). Значение 2A1
достигается тогда, когда фазы складываемых
колебаний совпадают, а нуль - когда фазы
противоположны. Периодическое изменение
результирующей амплитуды, получающееся
при сложении колебаний, совершающихся
с близкими частотами и вдоль одной
прямой, называют биениями. Циклическая
частота биений Ω=
|ω1
-
ω2
|,
период биений Т
= 2π/
Ω (рис.3) и
частота биений
νб = 1/Tб = |ν1 - ν2 |, где ν1 и ν2- частоты складываемых колебаний.
Рис. 4.
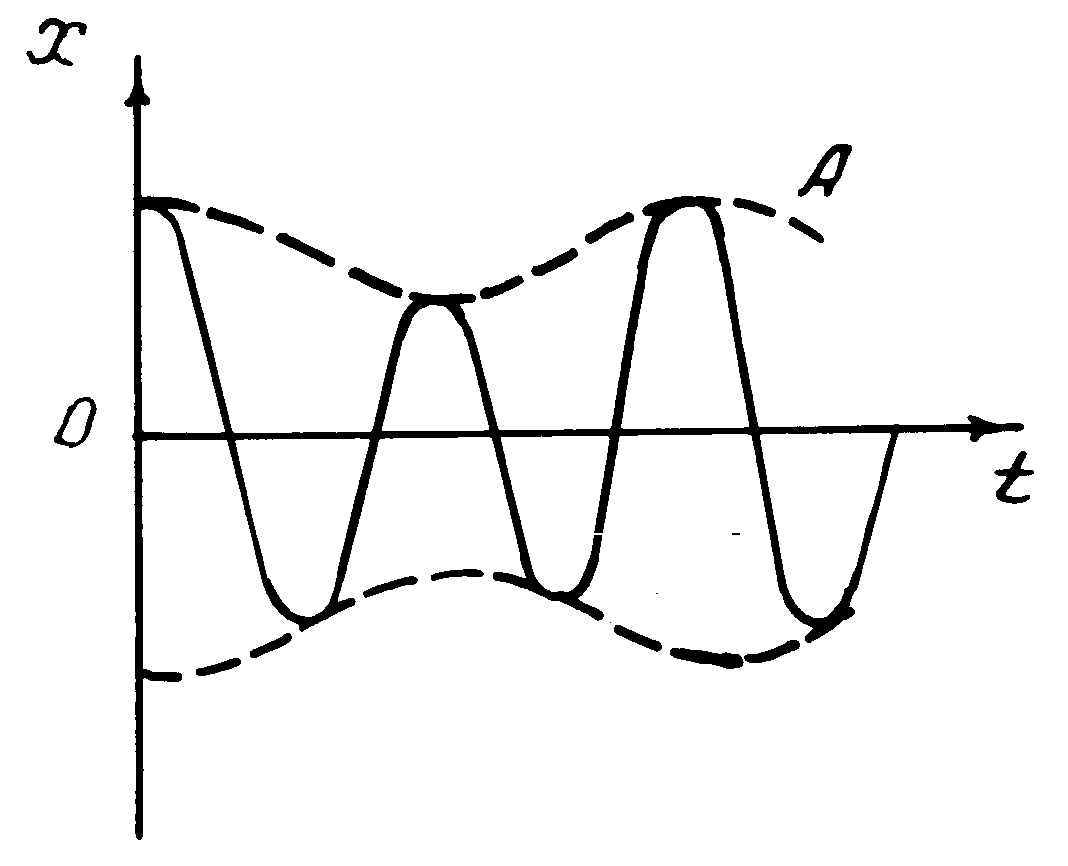
Если амплитуды складываемых колебаний не равны (A1 # A2), то максимальное значение амплитуды результирующего колебания равно A1+A2, а минимальное А1-А2. В этом случае биения выражены менее четко (рис.4). Частоты Ω, νб и период Tб определяются разностью частот складываемых колебаний и не зависят от их амплитуд и начальных фаз.
Сложение колебаний во взаимно перпендикулярных направлениях.
Представим две взаимно перпендикулярные векторные величины x и y, изменяющиеся со временем с одинаковой частотой ω по гармоническому закону
![]()
![]() (6)
(6)
где ex и eу — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия. В случае колеблющейся частицы величины
![]() ,
,
![]() , (7)
, (7)
определяют координаты частицы на плоскости xy. Частица будет двигаться по некоторой траектории, вид которой зависит от разности фаз обоих колебаний. Выражения (6) представляют собой заданное в параметрической форме уравнение этой траектории. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (6) параметр t. Из первого уравнения следует, что
![]() (8)
(8)
Соответственно
![]() (9)
(9)
Развернем косинус во втором из уравнений (6) по формуле для косинуса суммы:
![]()
Подставим вместо cosωt и sinωt их значения (3) и (4):
![]()
![]()
Преобразуем это уравнение
![]()
![]()
![]()
![]() (10)
(10)
Это уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз α.
Попробуем найти форму траектории для нескольких частных случаев.
Разность фаз α равна нулю.
В этом случае уравнение (10) упрощается следующим образом:
![]() (11)
(11)
Отсюда получается уравнение прямой:
![]()
Результирующее
движение является гармоническим
колебанием вдоль этой прямой с частотой
ω и амплитудой, равной
![]() (рис. 5а).
(рис. 5а).
Разность фаз α равна ±π.
Уравнение (10) имеет вид
![]() (12)
(12)
Следовательно, результирующее движение представляет собой гармоническое колебание вдоль прямой
![]() (рис.
5б)
(рис.
5б)
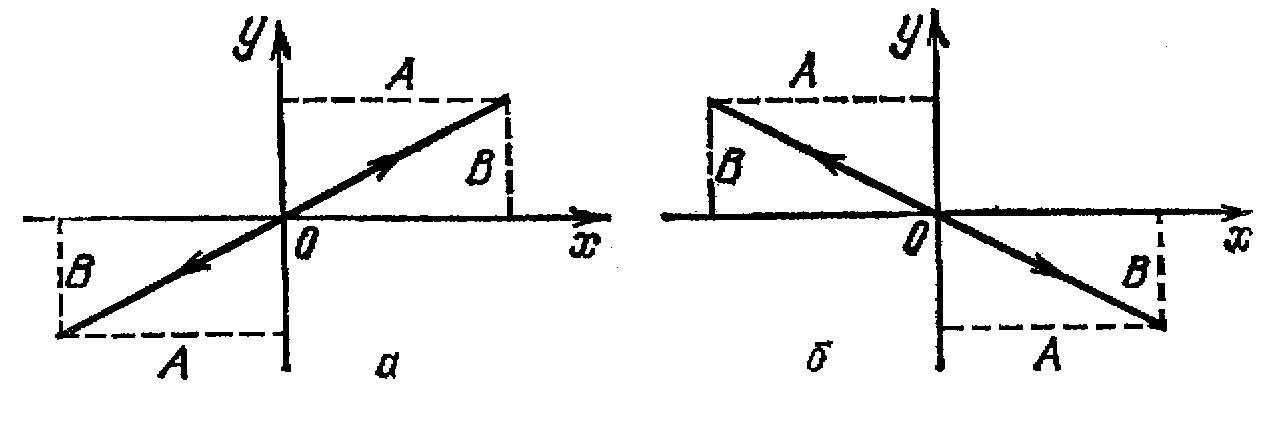
Рис.5.
Разность фаз
 .
.
Уравнение (10) переходит в уравнение эллипса, приведенного к координатным осям:
![]() (13)
(13)
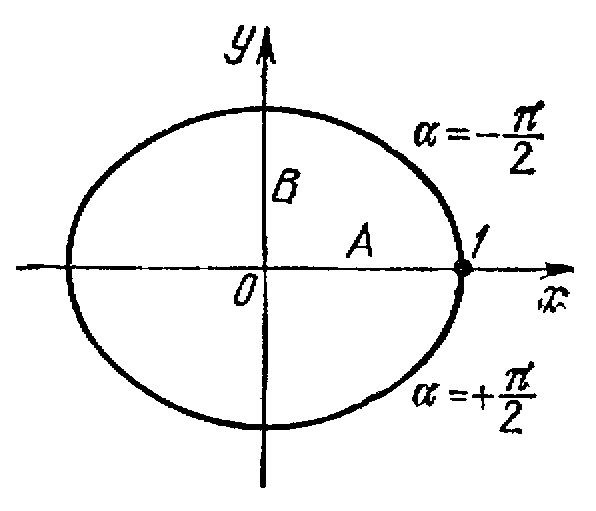
Рис.6.
Полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд А и В эллипс превращается в окружность.
Случаи
![]() и
и
![]() отличаются
направлением движения по эллипсу
или окружности.
отличаются
направлением движения по эллипсу
или окружности.
Следовательно, равномерное движение по окружности радиуса R с угловой скоростью ω может быть представлено как сумма двух взаимно перпендикулярных колебаний:
![]() ,
,
![]()
(знак плюс в выражении для у соответствует движению против часовой стрелки, знак минус — движению по часовой стрелке).
Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют вид сложных кривых, называемых фигурами Лиссажу.
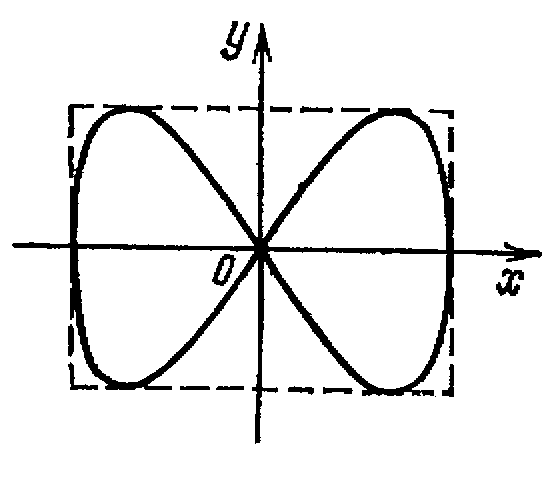
Рис.7. Фигура Лиссажу для
отношения частот 1:2 и
разности фаз π/2

Рис.8. Фигура Лиссажу для отношения частот 3:4
и разности фаз π/2
Наблюдать биения и фигуры Лиссажу можно с помощью электронного осциллографа и звуковых генераторов.
