Лабораторная работа № 5. Деформации сдвига и кручения.

Задание : определить модуль сдвига меди методом крутильных колебаний кольца.

Оборудование и принадлежности: установка для проведения измерений, секундомер, линейка, штангенциркуль.

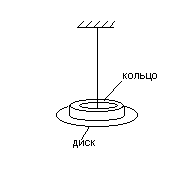Рис. 7

Описание установки

К нижнему концу проволоки из исследуемого материала (рис. 1) прикрепляют массивный диск, на который помещают кольцо так, чтобы его центр находился на оси вращения системы (диск располагается горизонтально).

Элементы теории.

Рис. 8

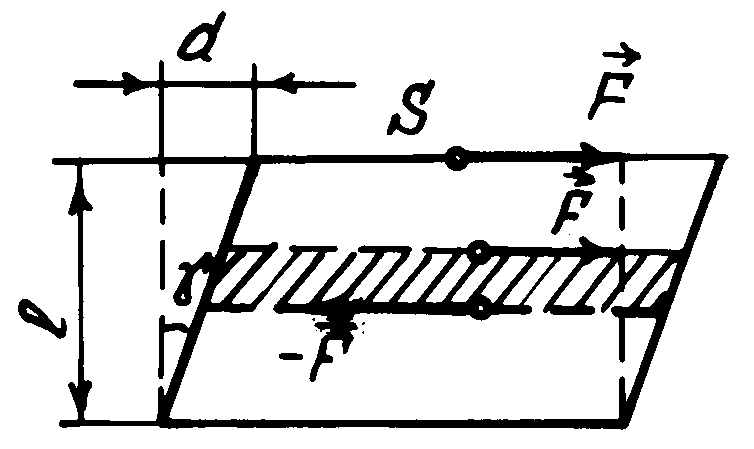
Деформация сдвига. Под воздействием силы , распределенной по площади верхней граниS и направленной параллельно ей, горизонтальные слои однородного тела (бруска) смещаются друг относительно друга (рис. 2). Это - деформация сдвига. Вертикальные грани бруска остаются плоскими, но наклоняются на некоторый угол g - угол сдвига. Количественной мерой абсолютной деформации сдвига является смещение верхней грани d. Величина смещения зависит, в частности, от высоты бруска l. Мерой относительной деформации служит величина d/l = tgg. При малых деформациях tg g » g.

Мысленно выделим в бруске произвольный тонкий горизонтальный слой (см. рис. 2). На него со стороны соседних слоев действуют две антипараллельные силы упругости и. Их модули в силу равновесия равны между собой (||=|-|= F). Величина

t = F/S (1)

называется тангенциальным напряжением. Здесь S- площадь, на которую действует равномерно распределенная упругая сила F. При неравномерном распределении силы , гдеdS - элементарно малая площадка; dF - модуль силы упругости, действующей на площадку dS параллельно ей.

Зависимость между углом сдвига и приложенным тангенциальным напряжением изображена на рис. 3. Для одного и того же материала она сходна с зависимостью между нормальным напряжением d и относительным удлинением e.

При малых упругих деформациях возникшее в теле

Рис. 9

тангенциальное напряжение

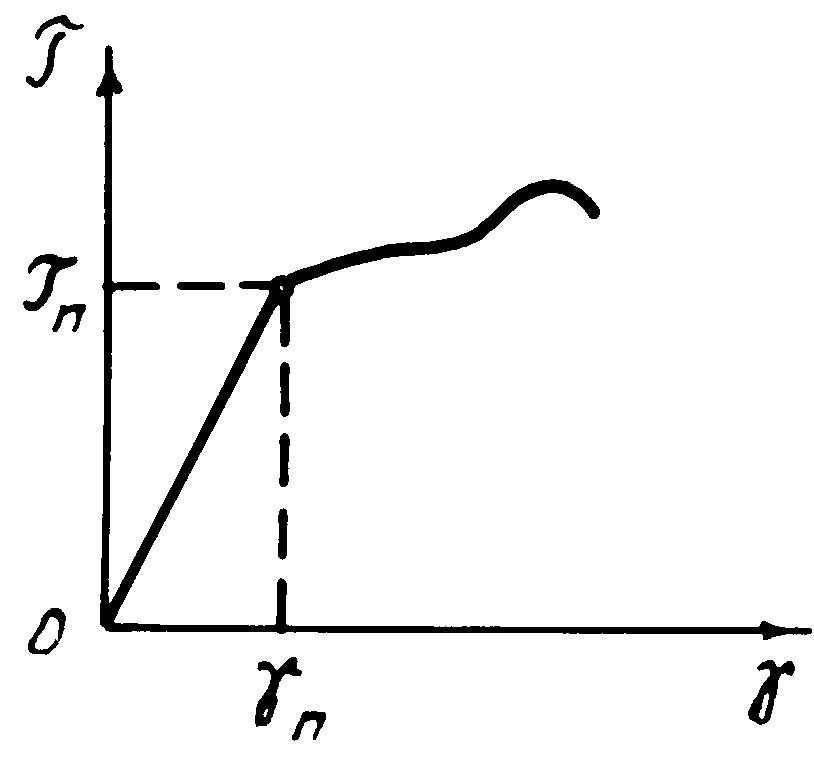
(от 0 до t_i) прямо пропорционально

углу сдвига (от 0 до g_n) – Закон Гука

для деформации сдвига:

t = G g(2)

Рис. 10

Коэффициент G зависит от свойства материала и его физического состояния. Он называется модулем сдвига вещества, из которого изготовлено тело.

Деформация кручения. Пусть верхнее основание однородного стержня (например, проволоки) радиусом R и длиной L закреплено, а нижнее закручено вокруг оси O₁O на угол j_o (рис. 4). Такая деформация называется кручением.

Мерой абсолютной деформации кручения является угол закручивания j, который неодинаков в различных поперечных сечениях стержня (удаленных на разные расстояния l от верхнего основания). Величина принимается за меру относительной деформации кручения. Для однородного стержня при малых деформациях она одинакова во всех сечениях.

При закручивании стержня его поперечные слои испытывают сдвиг относительно друг друга. Эта деформация неоднородна: в точках, расположенных на различных расстояниях r от оси O₁O, угол сдвига разный (см. рис. 4). На поверхности стержня этот угол максимальный и равен, на оси стержня он равен нулю.

Таким образом, деформацию кручения можно рассматривать как неоднородную деформацию сдвига. При малых деформациях угол сдвига

(3)

В соответствии с законом Гука (2) тангенциальное напряжение

. (4)

Отсюда

(5)

Рис. 11

Следовательно, на разных расстояниях r от оси возникающие силы упругости, действующие на одинаковые площадки dS, различны.

На верхнее и нижнее основания любого малого элемента стержня длиной dl (рис. 5) со стороны соседних частей стержня действуют силы упругости dF, определяемые соотношением (5). При равновесии модуль суммарного момента всех сил, действующих на верхнее основание, равен модулю момента сил, действующих на нижнее основание, т.е. модуль момента сил упругости в любом сечении однородного стержня одинаков. Рассчитаем его значение. Для этого в сечении стержня выделим площадку (заштрихована на рис. 6)

(6)

Рис. 12

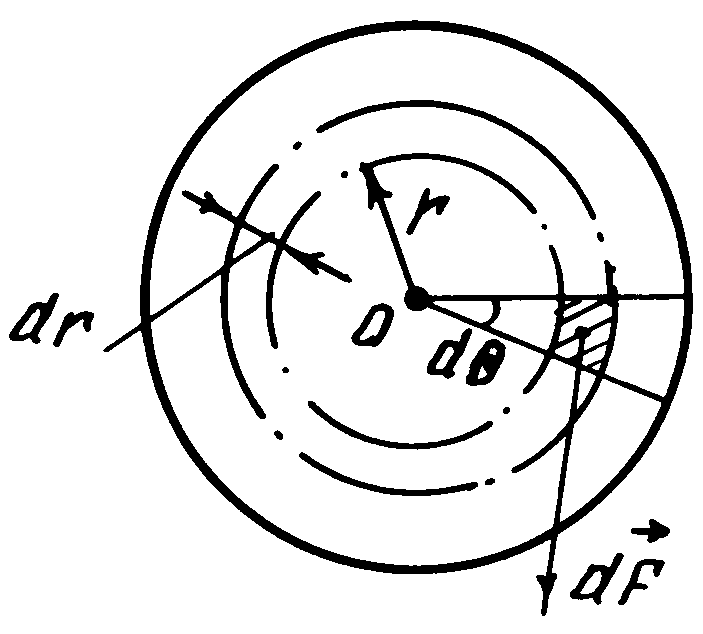
на которую действует сила упругости . Момент этой силы относительно оси стержня равен

(7)

Тогда с учетом (5) - (7)

(8)

Для нижнего основания стержня момент сил

(9)

Коэффициент

, (10)

где d - диаметр проволоки, зависит не только от материала и его физического состояния, но и от геометрических размеров стержня. Для данного стержня эта величина постоянная и называется модулем кручения. Соотношение М = D j₀ - Закон Гука для деформации кручения.

Как следует из (9), толстые короткие стержни трудно подвергнуть закручиванию и, наоборот, длинные тонкие проволоки под воздействием даже очень малых моментов закручиваются на заметный угол. Этим пользуются при создании чувствительных подвесных систем в измерительных приборах.

Экспериментально модуль кручения D проволоки можно измерить при помощи крутильных колебаний тяжелого тела, подвешенного к ее концу. Уравнение движения для этого случая запишется в виде

(11)

где J –момент инерции системы относительно оси вращения; – сумма моментов (относительно той же оси) всех сил, действующих на систему;–угловое ускорение. Если силами трения можно пренебречь, то в сумме остается только один момент упругих сил, модуль которого при малых амплитудах определяется соотношением (9). Этот момент сообщает системе угловое ускорение, направленное противоположно угловому смещению. Поэтому моментМ следует взять со знаком минус. Тогда (11) приобретает вид

(12)

Уравнение (12) математически тождественно уравнению гармонических колебаний с циклической частотой :

(13)

Следовательно, система будет совершать гармонические колебания с частотой . Период колебаний

(14)

Отсюда по известному моменту инерции J и периоду ее малых колебаний Т можно определить модуль кручения D и связанный с ним модуль сдвига G(формула 10).

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА ПРИ ПОМОЩИ

КРУТИЛЬНЫХ КОЛЕБАНИЙ КОЛЬЦА

Теория метода. Период малых крутильных колебаний системы измеряют дважды: сначала без кольца, а затем с кольцом. В первом случае в соответствии с (14) период колебаний

(15)

во втором -

(16)

где J₁ –момент инерции системы без кольца; – момент инерции кольца относительно оси, перпендикулярной к его плоскости и проходящей через центр кольца;m – масса кольца; R₁ и R₂ – его внешний и внутренний радиусы.

Из этих соотношений получаем:

с учетом (10) получаем окончательно:

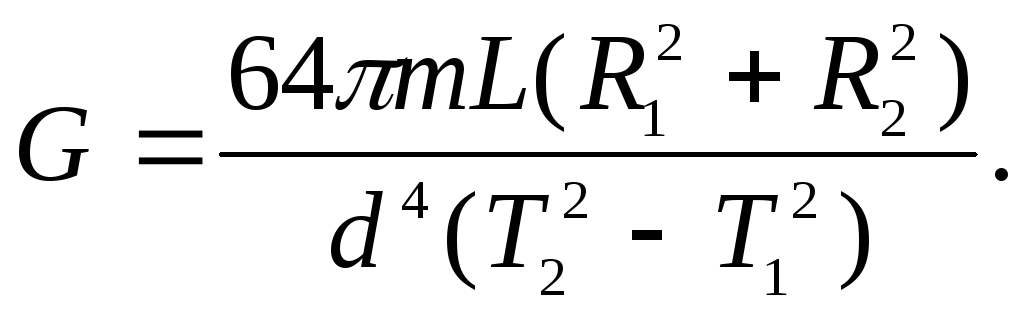(17)