
- •Определение земного ускорения свободного падения при помощи оборотного и математического маятников.
- •Результаты измерений и расчётов ускорения свободного падения с помощью математического маятника.
- •Сложение гармонических колебаний
- •1. Биения.
- •Порядок выполнения задания.
- •1.Изучить биения.
- •2.Изучить сложение взаимно перпендикулярных колебаний.
- •Лабораторная работа № 5. Деформации сдвига и кручения.
- •Элементы теории.
- •Порядок выполнения задания.
- •Контрольные вопросы:
- •Литература:
- •Измерение температуры электрическими контактными термометрами.
- •Температурные шкалы и единицы измерения.
- •Электрические контактные термометры
- •1. Металлические термометры сопротивления.
- •2. Полупроводниковые термометры сопротивления.
- •3. Термоэлектрические термометры.
- •Порядок выполнения задания.
- •Порядок выполнения работы
- •Лабораторная работа№7
- •Лабораторная работа № 9. Изучение методов измерения оптических показателей преломления твердых тел.
- •Контрольные вопросы:
- •Литература.
- •Лабораторная работа№10
- •Тогда из (1) получаем
- •Таким образом, задерживающее напряжение Uз линейно зависит от частоты падающего на фотоэлемент излучения.
- •1. Собрать схему с сопротивлением r (рис.1). Переключатели пределов шкалы вольтметра и амперметра установить на максимальные значения.
- •Лабораторная работа № 12. Поглощение света в жидких и твердых веществах.
- •Контрольные вопросы:
- •Литература:
- •Лабораторная работа № 13 определение показателя преломления жидкостей с помощью рефрактометра.
- •3.Порядок работы.
- •Контрольные вопросы.
- •Литература.
- •Лабораторная работа № 14. Определение концентраций водных растворов сахара по вращению плоскости поляризации.
- •Литература.
- •Лабораторная работа № 15.
- •При вычислении введем вспомогательную переменную
- •Отсюда постоянная Стефана-Больцмана
- •Вопросы.
- •С учетом этого замечания соотношение (2) следует записать в виде
- •Контрольные вопросы.
- •Литература.
Тогда из (1) получаем
![]() . (4)
. (4)
Таким образом, задерживающее напряжение Uз линейно зависит от частоты падающего на фотоэлемент излучения.
Задание:
Изучение внешнего фотоэффекта.
В разъем для фотоприемника вставить вакуумный фотоэлемент.
В кассету вставить нейтральный светофильтр с наименьшей оптической плотностью D . Не меняя нейтральный светофильтр, увеличить напряжение на электродах фотоэлемента, сила тока при этом должна возрастать. При некотором напряжении она достигнет максимального значения
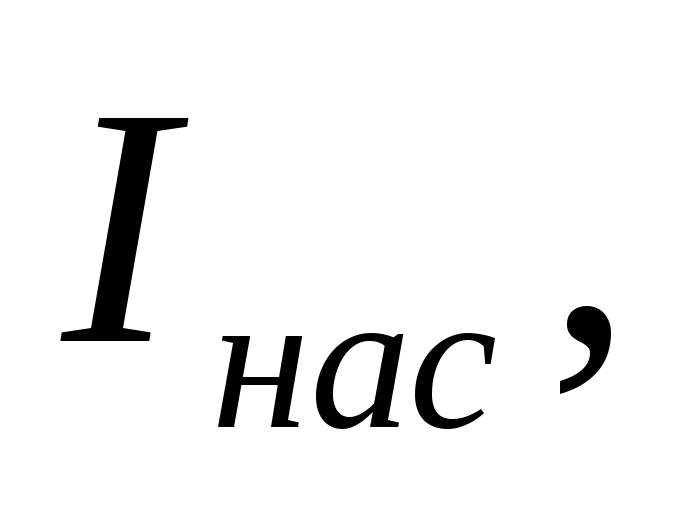 после чего перестанет увеличиваться.
после чего перестанет увеличиваться.
Меняя
нейтральные светофильтры, получить
разные значения тока насыщения
![]() для
каждого светофильтра. Результаты
измерений занести в таблицу и построить
графики зависимостей силы токаI
от напряженияU.
для
каждого светофильтра. Результаты
измерений занести в таблицу и построить
графики зависимостей силы токаI
от напряженияU.
Таблица1
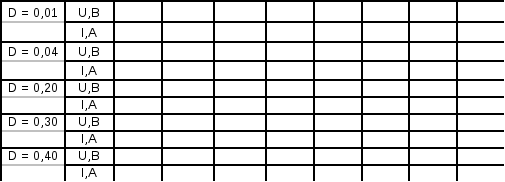
Вставить в кассету фиолетовый светофильтр, подать напряжение на электроды фотоэлемента. Меняя цветные светофильтры в порядке очередности от наименьшей пропускаемой длины волны до наибольшей зафиксировать значение силы фототока. Выбрать светофильтр, при установке которого была зафиксирована наименьшая сила тока, но не равная нулю. Пропускаемое этим светофильтром излучение с длиной волны
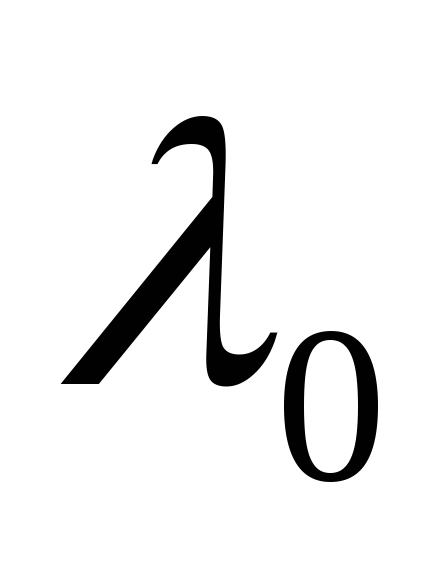 ,
и будет являться «красной» границей
или длинноволновым порогом фотоэффекта.
,
и будет являться «красной» границей
или длинноволновым порогом фотоэффекта.
Результаты измерений занести в таблицу 2. Построить график зависимости силы фототока I,mA от длины волны,нм пропускаемого излучения.
Таблица 2

Вставить в кассету светофильтр. Изменить полярность фотоэлемента на обратную. При некотором значении напряжения Uз обратной полярности сила тока уменьшится до нуля. Измерив задерживающее напряжение, найти значение максимальной кинетической энергии фотоэлектронов по формуле:
![]()
Результаты измерений занести в таблицу 3.
Построить график зависимости максимальной начальной кинетической энергии E*10-19,Дж фотоэлектронов от частоты *1014,Гц пропускаемого излучения.
Таблица 3

Контрольные вопросы:
Какие основные законы внешнего фотоэффекта?
Что называется работой выхода электрона из вещества?
Чем отличаются между собой вольт-амперные характеристики фотоэлемента, полученные при его облучении светом различных длин волн?
Литература:
Физический практикум. Под ред. Кембровского Г. С.-Минск: «Университетское», 1986.
Сивухин Д.В. Общий курс физики. Оптика. М.: Наука.
Трофимова Т.И. Курс физики. –М.: Высшая школа. 1997.
Лабораторная работа № 11.
Закон Ома для переменного тока.
Цель: определить сопротивление, емкость и индуктивность в цепи переменного тока.
Оборудование и принадлежности: источник питания, вольтметр, амперметр, активное сопротивление, конденсатор, катушка индуктивности.
ТЕОРИЯ. Переменный электрический ток - это установившиеся вынужденные электромагнитные колебания. Переменным называется ток, сила, направление и (электродвижущая сила)ЭДС которого периодически изменяются. Периодом Т(с) называется время полного колебания ЭДС. Величина, обратная периоду – частота колебаний (Гц). Переменный ток характеризуют также циклической частотой =2=2/Т. Циклическая частота определяет число колебаний, которые происходят за 2 секунд. Для городской эдектросети эти параметры имеют следующие значения: =50 Гц, Т=0,02 с, =314 с-1 с отклонением 1%.
Переменный ток промышленной частоты можно считать квазистационарным, т.е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, так как их изменения происходят достаточно медленно, а электромагнитные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются Закон Ома и вытекающие из него правила Кирхгофа.
Мгновенные значения силы тока и напряжения в цепи изменяются по гармоническому закону:
I= I0 sin (t+ i); U=U0 sin (t+ u); (1)
где I0 и U0 -амплитуды силы тока и напряжения, то есть максимальные по модулю значения, i и u – их начальные фазы. В общем случае они не совпадают между собой. Приборы переменного тока обычно измеряют эффективные(действующие) значения напряжения и тока, которые равны
Iэф.= I0/2; Uэф= U0/2; (2)
Между эффективными значениями тока и напряжения существует связь
Iэф.= Uэф/Z (3)
Величина Z называется полным сопротивлением цепи. Выражение (3) есть закон Ома для цепи переменного тока.
1.Сопротивление в цепи переменного тока.
Рассмотрим случай, когда источник переменного тока замкнут на внешнюю цепь, имеющую настолько малые индуктивность и емкость, что ими можно пренебречь. В цепи имеется переменный ток I= I0 sin t.
Найдем, по какому закону изменяется напряжение между точками а и б (рис.1). Применяя закон Ома, имеем U= I R= I0 R sin t.
 А а
А а








U V R



б
Рис.1
Таким образом, напряжение на концах участка цепи изменяется также по закону синусов, причем разность фаз между колебаниями тока и напряжения равна нулю. Напряжение и ток одновременно достигают максимальных значений и одновременно обращаются в нуль (рис.2).
Максимальное значение напряжения U0= I0 R.

Рис.2
Гармонически изменяющиеся величины удобно наглядно изображать при помощи векторных диаграмм. Выберем ось диаграммы так, чтобы вектор, изображающий колебания тока, был направлен вдоль оси токов. Тогда вектор напряжения будет также направлен вдоль оси токов , так как разность фаз между током и напряжением равна нулю (рис.3). Длина этого вектора равна амплитуде напряжения U0= I0 R.
 0 U0=
I0 R
0 U0=
I0 R

 ось
токов
ось
токов
Рис.3
2. Ёмкость в цепи переменного тока.
Пусть участок цепи содержит конденсатор ёмкостью С, причём
сопротивлением и индуктивностью участка можно пренебречь (рис.4).
 U
U




V




 а б
а б





A
 I
I
С
Рис.4
Емкость конденсатора измеряется зарядом, находящимся на каждой из обкладок, если напряжение между обкладками равно единице, тогда С= q/U. Единицей емкости в системе СИ служит фарада (Ф). 1Ф= 1 Кл/В. Емкость конденсатора зависит от его размеров, формы и диэлектрической проницаемости среды, разделяющей обкладки.
Если сила тока в цепи изменяется по закону
I= I0 sin wt (4)
то из I= dq/dt следует, что q= I0 sin t dt = - I0/ * cos t + q0.
Положим q0 =0. Следовательно,
U= - I0 / C *cos t = I0 / C *sin (t -/2) (5)
Сравнивая (4) и (5), мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону синуса, но колебания напряжения на конденсаторе отстают по фазе от колебаний тока на /2 (рис.5).
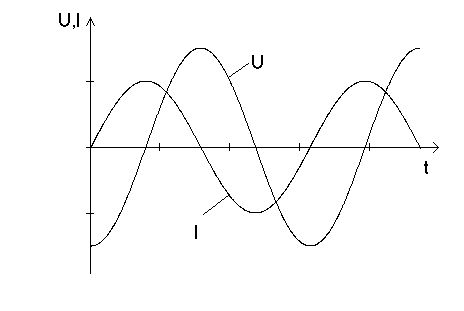
Рис.5
Напряжение на конденсаторе в какой-то момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебания. Поэтому колебания напряжения запаздывают относительно колебаний тока. Пусть в момент t=0 сила тока равна нулю, но на конденсаторе ещё имеется отрицательный заряд, перенесенный током в предыдущий период времени, и напряжение не равно нулю. Для обращения в нуль этого заряда необходимо, чтобы некоторое время t проходил ток положительного направления, и поэтому, когда заряд конденсатора ( а значит, и напряжение) станет равным нулю, сила тока уже не будет равна нулю.
Из формулы (5) амплитуда колебаний напряжения на конденсаторе равна U0= I0/С.
Cравнивая это выражение с законом Ома для участка цепи с постоянным током (U= I R), мы видим, что величина
Zc= 1/С
представляет собой сопротивление конденсатора для переменного тока, т.е. емкостное сопротивление. Оно обратно пропорционально круговой частоте тока и величине емкости. Чем больше емкость конденсатора и чем чаще изменяется направление тока (т.е. чем больше круговая частота ), тем больший заряд проходит за единицу времени через поперечное сечение подводящих проводов. Следовательно, I С. Но сила тока и сопротивление обратно пропорциональны друг другу, тогда сопротивление Zc 1/С.

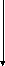 О
I
О
I
-/2
U0= I0/С
Рис.6
Полученные результаты представим в виде векторной диаграммы (рис.6). Здесь вектор, изображающий колебания напряжения, повернут относительно оси токов в отрицательном направлении ( по часовой стрелке) на угол /2. Длина этого вектора равна амплитуде напряжения U0= I0/С.
3. Индуктивность в цепи переменного тока.
Рассмотрим случай, когда участок цепи содержит только индуктивность (рис.7).



 U
U




 V
V


 L A
L A
 I
I
Рис.7
При наличии переменного тока в катушке индуктивности возникает э.д.с. самоиндукции , и поэтому мы видим, что, применив Закон Ома для участка цепи с э.д.с., получим: U= I r - . При r0 (омическое сопротивление цепи пренебрежимо мало) и = -LdI/dt будем иметь U= LdI/dt . Если сила тока в цепи изменяется по закону синуса
I= I0 sin t (6)
то U= I0 L cos t= = I0 L sin (t + /2) (7)
Сравнивая (6) и (7), видим, что колебания напряжения на индуктивности опережают по фазе колебания тока на p/2. Когда сила тока, возрастая, проходит через нуль, напряжение уже достигает максимума, после чего начинает уменьшаться; когда сила тока становится максимальной, напряжение проходит через нуль и т.д. (рис.8).

Рис. 8
Индуктивность контура равна связанному с ним магнитному потоку, если в контуре идет ток, равный единице (L= Ф/I). Единицей индуктивности в системе СИ служит Генри (1 Гн= 1 Вб/А). Индуктивность зависит от формы и размеров контура и от магнитной проницаемости среды.
Сдвиг фаз обусловлен тормозящим действием электродвижущей силы самоиндукции: она препятствует как нарастанию, так и убыванию тока в цепи, поэтому максимум тока наступает позднее, чем максимум напряжения. Наличие омического сопротивления привело бы к уменьшению сдвига фаз. Из (7) следует, что амплитуда напряжения равна U0= I0 L и, следовательно, величина ZL=wL играет ту же роль, что и сопротивление участка. Она представляет собой индуктивное сопротивлениекатушки.
Оно пропорционально круговой частоте тока и величине индуктивности. Эта зависимость объясняется тем, что индуктивное сопротивление обусловлено действием электродвижущей силы самоиндукции, уменьшающей эффективный ток и, следовательно, увеличивающей сопротивление. Величина же этой э.д.с. ( следовательно, сопротивления) пропорциональна индуктивности катушки L и скорости изменения тока, т.е. круговой частоте .
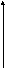
 U0=I0
L
U0=I0
L
/2
О I
Рис. 9
Полученные результаты представим на векторной диаграмме (рис.9). Вектор, изображающий колебания напряжения, повернут относительно оси токов в положительном направлении (против часовой стрелки) на угол /2, а его длина равная амплитуде есть I0 L.
4. Закон Ома для переменных токов.
Пользуясь результатами, полученными в п.п. 1-3, можно найти соотношение между колебаниями тока и напряжения в любой цепи.
Рассмотрим последовательное соединение сопротивления, емкости и индуктивности (рис.10). Ток в цепи изменяется по закону синуса I= I0 sin wt .
Вычислим напряжение между концами участка цепи. Так как при последовательном соединении проводников складываются напряжения, то искомое напряжение и есть сумма трех напряжений: на сопротивлении, емкости и индуктивности, причем каждое изменяется по закону синуса.



 а А R
а А R






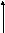


 C
C


 U V I
U V I


 б
L
б
L
Рис. 10
Для сложения этих трех гармонических колебаний воспользуемся векторной диаграммой напряжений. Колебания напряжения на сопротивлении изображаются на ней вектором Uа, направленном вдоль оси токов, колебания же напряжения на индуктивности и емкости – векторами, перпендикулярными к оси токов, с длинами I0 L и I0/ C.
Складывая два последних колебания, получим одно, изображаемое вектором Uр, перпендикулярным к оси токов и имеющим длину
Up= I0 (L- 1/C).
Полное напряжение можно рассматривать как сумму двух гармонических колебаний: напряжения Ua (активная составляющая напряжения), совпадающего по фазе с током, и напряжения Uр (реактивная составляющая напряжения), отличающегося по фазе на /2 (рис.11).
 I0
L
I0
L


U0
Up=I0(L – 1/C)

 О
I
О
I
Ua=I0 R
I0/C
Рис. 11.
Оба эти колебания, складываясь, дают гармоническое колебание
U= U0 sin (t+), (8)
которое изображается векторной суммой векторов Uа и Up, причем длина результирующего вектора равна амплитуде напряжений U0, а угол, образованный результирующим вектором с осью токов, - сдвигу фазы между током и напряжением .
Из треугольника напряжений получаем:
U0= I0 R2+(L – 1/C)2 (9)
Из рис.11 следует tg = (L – 1/C)/ R (10)
Полное сопротивление в цепи переменного тока
![]()
(11)
Активное сопротивление участка цепи
R = Z cos (12)
Реактивное сопротивление цепи
= Z sin = L – 1/C (13)
Наличие реактивного сопротивления не сопровождается выделением тепла. Соотношения (10,11,12,13) можно получить из прямоугольного треугольника, который называется треуголником сопротивлений (рис. 12).


Полное
сопротивление Z Реактивное
сопротивление

Активное
сопротивление R
Рис. 12
В таблице 1 приведены полное сопротивление и фазовый сдвиг для цепей с различными комбинациями активного сопротивления R (Oм), индуктивности L (Гн), емкости С (Ф). Самым общим случаем в таблице является случай 6. Все остальные получаются из него как частные.
Таблица 1.
|
№ п/п |
Схема цепи |
Вклю-чены |
Полное сопротивление |
Фазовый сдвиг |
Примечание |
|
1.
2.
3.
4.
5.
6. |
|
R(Ом)
L (Гн)
C (Ф)
R (Oм) С (Ф)
R(Ом) L(Гн)
R(Ом) L(Гн) С(Ф) |
Z = R
ZL= L
ZC = 1/C
Z = R2 +(1/C)2
Z=R2 + (L)2
Z= R2 +(L-1/C)2 |
= 0
= /2
= - /2
tg
=
tg = L/R
tg=(L – 1/C)/ R |
Ток по фазе совпадает с напряжением
Напряжение опережает ток на Т/4
Напряжение отстает от тока на Т/4
Напряжение отстает от тока
Напряжение опережает ток
Напряжение отстает или опережает ток в зависимости от преобладания емкостного (1/C) или индуктивного (L) cопротивлений.
|
Порядок выполнения задания.
