Графическое изображение зависимостей комплексных величин от параметров

В некоторых случаях вместо зависимости модуля и угла в декартовой системе координат можно построить зависимости от параметра действительной и мнимой части исследуемой комплексной величины. Если изменение модуля сопротивления при постоянном угле φ изображается прямой линией образующей с действительной осью комплексной плоскости угол φ, то изменение угла φ при неизменном модуле сопротивления изображается окружностью с радиусом. Рассмотрим диаграммы сопротивления и проводимости электрической цепи с последовательным, параллельным или смешанным соединением сопротивлений при изменении одного параметра.

1. Последовательное соединение сопротивлений: а) б)

Рис.1.26 Схемы электрических цепей а, б и их ВД при изменении по величине активного сопротивления

Из анализа ВД на рис.1.26 следует, что при изменении сопротивления “” геометрическим местом точек (ГМТ) комплексного сопротивлениябудет прямая параллельная оси вещественных чисел над или под осью абсцисс, в зависимости от характера реактивного сопротивления.

Геометрическим методом точек комплексной проводимости будет полуокружность, проходящая через начало координат комплексной плоскости, причем диаметр этой полуокружности обратно пропорционален реактивному сопротивлению –.

Части полуокружностей, соответствующие отрицательным значениям r, из рассмотрения исключаются.

Значению соответствует наиболее удаленная точка дуги полуокружности, т.к.проводимость возрастает до бесконечности при малом Х.

_{Значению} соответствует точка в начале координат, т.к.

Если активное сопротивление – неизменно (рис.1.27, 1.28), а переменным по величине является реактивное сопротивление, то, как и в первом случае ГМТ комплексного сопротивления будет прямая, но теперь уже параллельная оси мнимых чисел.

ГМТ конца вектора будет окружность, проходящая через начало координат комплексной плоскости, причем диаметр окружности будет равен– активной проводимости.

При цепь имеет только активное сопротивление и соответственно проводимость. Припроводимость цепи будет равна 0.

Рис.1.27 КВД в случае переменного реактивного сопротивления

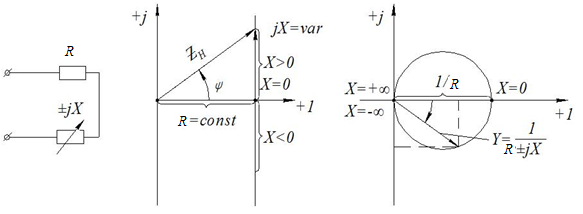
а) б) в)

Рис.1.28 Схема с переменным реактивным сопротивлением (а), треугольник сопротивлений (б), когда и КВД (в)

2. Параллельное соединение сопротивлений:

При параллельном соединении элементов (рис.1.29) КВД строится для комплексного сопротивления . ГМТ для комплексной проводимости будут прямые линии, т.е. линейные ВД.

Дело в том, что при параллельном соединении складываются проводимости, следовательно для схемы приведенной ниже, получим Изобразим ГМТ.

а) б) в)

_{Рис.1.29 Схема с параллельным соединением элементов (а) когда} , треугольник проводимостей (б) и КВД сопротивлений (в), когда

При изменении реактивного сопротивления (рис.1.30), геометрическое место точек конца вектора комплексной проводимости будет прямая параллельная оси мнимых чисел, а ГМТ конца вектора– полуокружности с диаметромпроходящие через начало координат.

При полное сопротивление в электрической цепи равно нулю. Присопротивление и проводимость цепи являются активными.

а) б) в)

_{Рис.1.30 Схема с параллельным соединением элементов, (а) когда} , треугольник проводимостей (б) и КВД сопротивлений когда

3. Смешанное соединение сопротивлений (рис.1.31):

а) б)

_{Рис.1.31 – Схема со смешанным соединением элементов (а), когда} и КВД сопротивлений, когда

Пусть переменным параметром является реактивное сопротивление: ,.

Здесь КВД отличается от предыдущих тем, что окружность смещена относительно начала координат на величину сопротивления . Изменение « » может быть достигнуто изменением частоты или L, C параметров.