Порядок построения круговых диаграмм неразветвленных электрических цепей

Схема с последовательным соединением комплексных сопротивлений приведена на рис.1.21. Рассмотрим порядок построения для нее КВД токов.

1. Выбираем масштаб для напряжения и откладываем вдоль (непроявленной) оси ординат вектор, равный: ().

2. По закону Ома находим ток в электрической цепи:

.

3. Определяем ток в цепи при , т.е. при коротком замыкании нагрузки:.

Рис.1.21 – Схема с последовательным соединением комплексных сопротивлений

4) Выбираем масштаб тока и откладываем векторсо сдвигом на уголпо отношению к вектору напряжения. Хорда ОК это хорда круговой диаграммы тока.

5) Выбираем масштаб сопротивлений и вдоль хорды ОК откладываем отрезок.

6. Из точки А под углом к вектору тока короткого замыканияпроведем линию переменного параметра AN нагрузочного сопротивления.

7. Центр круговой диаграммы «С» можно получить двояко:

Вариант а. Провести касательную в точке «К» под углом и в точке «К» восстановим перпендикуляр до пересечения с перпендикуляром, восстановленным из середины хорды ОК.

Вариант б. Опустить из точки «О» перпендикуляр на линию переменного параметра AN. Тогда точка пересечения этого перпендикуляра с перпендикуляром восстановленным из середины хорды ОК даст центр КВД.

Определение центра окружности круговой диаграммы по второму варианту предпочтительнее, т.к. требует меньшего числа вспомогательных построений.

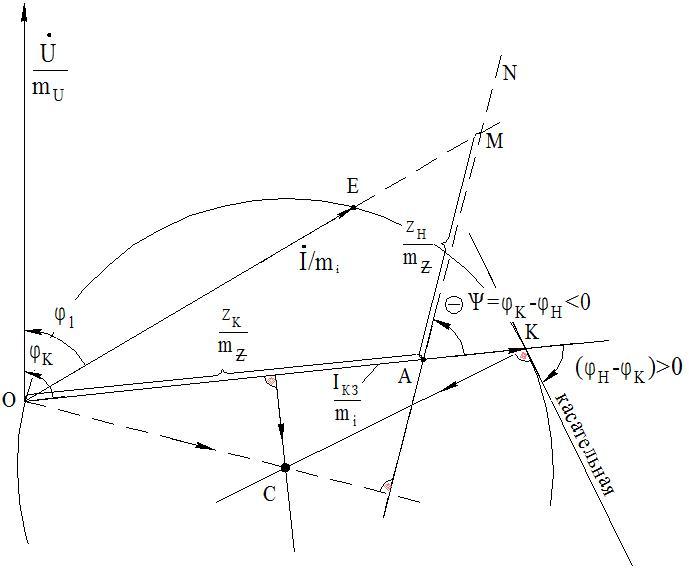
Рис.1.22 – КВД тока для схемы с последовательным соединением двух комплексных сопротивлений

8. Проводим дугу круговой диаграммы, радиусом ОС, а на линии AN откладываем отрезок .

9. Отрезок ОЕ в масштабе тока равен току в цепи. При измененииот 0 доток в цепи, изменяется по дуге окружности от 0 к К .

Круговая диаграмма для любой развлетвленной цепи

Круговую диаграмму можно построить для любой разветвленной электрической цепи, если в ней изменяется только одно сопротивление (рис.1.23).

Рис.1.23 Схема с активным четырехполюсником

Такую электрическую цепь всегда можно представить в виде четырехполюсника (ЧП). Если все элементы электрической цепи ЧП линейны, то токи на входе и выходе ЧП будут связаны линейными соотношениями:

Рассмотрим уравнение , вначале, в режиме ХХ (рис.1.23)., где «А» и «В» – комплексные числа. Пусть модуль сопротивления нагрузки– изменяется таким образом, чтобы. Тогда, рассматривая ЧП вместе с первичным контуром относительно зажимов сопротивления(рис.1.24) как активный двухполюсник (источник энергии с некоторым внутренним сопротивлением), – несложно показать, что конец вектора токапри изменениибудет описывать дугу окружности.

_{Чтобы определить комплексы «А» и «В» связывающие} , нужно знать значения токов для каких-нибудь двух крайних режимов: например, при

Рис.1.24 Схема замещения активного четырехполюсника

Рассмотрим уравнение , вначале в режиме холостого хода (рис.1.23).

1. При (обрыв), пусть при этом. Тогда из уравненияполучаем:.

2. При (короткое замыкание), пусть при этом. Тогда из уравненияполучим:или, откуда, тогда уравненияможет быть преобразовано к виду:.

На основании закона Ома для схемы двухполюсника (рис.1.24) получим:

где входное сопротивление всей цепи со стороны относительно зажимов сопротивления нагрузки.

Тогда по теореме об активном двухполюснике [1]:

, где .

С учетом последнего соотношения уравнение круговой диаграммы преобразуется к виду:

,

Уравнение может быть представлено круговой диаграммой с хордой. Для построения КВД необходимо предварительно определитьи(со стороны зажимов pq).

Порядок построения КВД ЧП:

1. Выбираем масштаб напряжения и откладываем вдоль непроявленной оси ординат.

2. Выбираем масштаб тока и откладываеми. Предположим при этом, что, а.

3. Соединяя концы векторов и, получаем хорду.

4. Выбирая масштаб , откладывали на хорде- отрезок.

5. Проводим прямую изменяющегося параметра под углом.

6. Опускаем перпендикуляр на из точкии восстанавливаем перпендикуляр из середины. Тогда точка пересечения двух перпендикуляров является центром круговой диаграммы “C”. Радиусомпроводим дугу окружности.

7. На линии переменного параметра откладываем сопротивление нагрузкии соединяем конец AN с точкой.

8. Точка пересечения линии с дугой окружности точки М при изменении сопротивления нагрузки перемещается по дугеОтрезокв масштабе тока дает ток в нагрузке, отрезок ОМ дает ток на входе ЧП. Отрезок МК в масштабе напряжения определяет напряжение в нагрузке.

9. Используя КВД можно определять и энергетические характеристики ЧП:

Рис.1.25 КВД токов и напряжений схемы с активным четырехполюсником активным четырехполюсником