
- •Министерство образования и науки Российской Федерации
- •Введение
- •Перечень условных обозначений
- •Основные теоретические положения
- •Четырехполюсники и круговые диаграммы
- •Характеристические параметры четырехполюсника
- •Характеристические сопротивления
- •Характеристическая постоянная или мера передачи чп
- •Передаточные функции чп
- •Круговые диаграммы четырехполюсника
- •Построение дуги окружности по хоорде и вписанному углу
- •Порядок нахождения центра окружности
- •Уравнение дуги окружности в комплексной форме записи
- •Понятие о круговой диаграмме электрической цепи
- •Круговая диаграмма для цепи из двух последовательно соединенных сопротивлений
- •Порядок построения круговой векторной диаграммы (квд) токов
- •Круговая диаграмма активного двухполюсника
- •Круговая диграмма тока для одной из ветвей параллельного контура
- •Порядок построения круговых диаграмм неразветвленных электрических цепей
- •Круговая диаграмма для любой развлетвленной цепи
- •Графическое изображение зависимостей комплексных величин от параметров
- •Электрические фильтры
- •Фильтры типа «»
- •Производные фильтры типа «»
- •2 Четырехполюсники и круговые диаграммы
- •2.1 Определение параметров пассивных четырехполюсников. Т и п – образные схемы замещения
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •2.2 Характеристические параметры четырехполюсников
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •2.3 Составные чп
- •Решение
- •Решение
- •2.4 Расчет активных четырехполюсников
- •Решение
- •Решение
- •Решение
- •2.5 Круговые диаграммы
- •Напряжение холостого хода на зажимах «pq»: , иначе:
- •2.6 Задачи смешанного типа
- •2.7 Задачи для самостоятельного решения
- •3 Электрические фильтры
- •3.1 Фильтры низкой частоты типа «k»
- •Для определения токов и построения векторной диаграммы, рассчитаем сопротивления фильтра на частоте :
- •3.2 Фильтры высокой частоты типа «k»
- •Рассчитаем сопротивления элементов фильтра на частоте:
- •3.3 Полосовые фильтры типа «k»
- •3.4 Заграждающие фильтры типа «k»
- •Производные фильтры типа «m»
- •3.6 Пассивные r – c фильтры
- •3.7 Задачи для самостоятельного решения
- •Список литературы
- •Оглавление
3.4 Заграждающие фильтры типа «k»
Задача
3.4.1
Определить полосу затухания заграждающего
фильтра (ЗФ), представленного на рис.3.4.1,
если параметры элементов фильтра
известны:
|
Рис.3.4.1 |
Решение Полоса затухания заграждающих фильтров, определяется соотношением[1,8]:
Откуда:
|
Задача
3.4.2
Определить полосу пропускания ЗФ,
представленного на рис.3.4.2, если параметры
элементов фильтра известны:
|
Рис.3.4.2 |
Решение Полосу затухания ЗФ можно определить, используя соотношение [1,8]: |
Откуда:
Задача
3.4.3
Определить параметры элементов
заграждающего фильтра, собранного по
П – образной схеме, если нижняя частота
среза равна 20 кГц, а верхняя 100 кГц,
номинальное характеристическое волновое
сопротивление=500 Ом.
Найти характеристическое сопротивление
фильтра
на частотах:
Построить зависимости
характеристического сопротивления
,
коэффициента затухания «α»
и коэффициента фазы «β»
от частоты. Рассчитать токи и напряжения
на заданной частоте и построить векторную
диаграмму токов и напряжений в элементах
ЗФ, если входной ток
равен 0,5 А.
|
Рис.3.4.3, а |
Решение
Схема заграждающего
фильтра, собранного по П – образной
схеме, приведена на рис.3.4.3. Зная
граничные частоты
|
Характеристическое
сопротивление
определяется следующим
образом [1,8]:
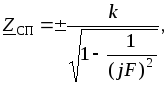 где
где
Рассчитаем характеристические сопротивления на заданных по условию задачи частотах.
На частоте
:
На частоте
На частоте
Для построения графической зависимости характеристического сопротивления, в функции частоты воспользуемся выражением [1,8]:
Коэффициент
затухания в полосе пропускания равен
нулю, а в полосе затухания определяется
соотношением:.
Коэффициент фазы в полосе пропускания
равен:
, а в полосе затухания:
где
. Графические
зависимости характеристического
сопротивления, коэффициента затухания
и коэффициента фазы от частоты приведены
на рис3.4.3,
б, в, г.
|
|
Рис.3.4.3,б |
|
Рис.3.4.3,в
| |
|
Рис.3.4.3,г
| |
Схема замещения ЗФ для расчёта токов и напряжений приведена на рис.3.4.3,д.
Определим
комплексные сопротивления
Для чего вначале найдем сопротивления отдельных элементов ЗФ:
|
|
|
Тогда сопротивления звеньев ЗФ в схеме замещения на рис.3.4.3,д:
Рассчитаем токи
и напряжения на обобщенных элементах
заграждающего фильтра, используя
характеристическое сопротивление
.
Вначале, используя
характеристическое сопротивление
и входной ток
, найдем входное
напряжение ЗФ
, а затем
ток
в параллельном входном
сопротивлении
:
В соответствии с
первым законом Кирхгофа найдем ток,
а затем определим падение напряжения
в последовательном сопротивлении ЗФ
Вычислим выходное
напряжение
и ток
в выходном параллельном
сопротивлении
|
Рис.3.4.3,е
|
Использупервый
закон Кирхгофа, найдем выходной ток
ЗФ
Векторная диаграмма токов и напряжений ЗФ показана на рис.3.4.3,е.
|
Задача
3.4.4
Определить характеристические параметры
заграждающего фильтра, собранного по
Т – образной схеме (рис.3.4.4.а) на частоте
если параметры элементов
ЗФ:
Вычислить токи и
напряжения на элементах ЗФ, если входное
напряжение
Построить
векторную диаграмму токов и падений
напряжений на заданной частоте, а также
графические зависимости коэффициента
затухания «α»,
коэффициента фазы «β»
и характеристического сопротивления
в функции частоты.
|
|
Решение Определим волновое номинальное характеристическое сопротивление фильтра:
|
Полоса задерживания заграждающих фильтров, определяется соотношением [8]:
Откуда получаем
частоты
,
и находим резонансную
частоту
ЗФ:
Вычисляем нормированную частоту ЗФ:
Тогда характеристическое сопротивление ЗФ:
Коэффициент фазы:
Для определения токов и напряжений элементов фильтра строим схему замещения ЗФ (рис.3.4.4,б), и рассчитываем сопротивления звеньев фильтра на заданной частоте:
|
|
Находим токи в элементах ЗФ: а) входной ток по закону Ома:
б) ток
|
в) Выходной ток
находим в соответствии
с первым законом Кирхгофа:
Для выходного контура составим уравнение по второму закону Кирхгофа и найдем выходное напряжение ЗФ:
Зная токи и сопротивления, вычисляем падения напряжений в элементах ЗФ:
|
Рис.3.4.4,в |
Векторная
диаграмма показана на рис. 3.4.4,в.
Зависимость коэффициента фазы от
частоты:
Зависимость коэффициента затухания
от частоты:
Зависимость
характеристического сопротивления
от частоты:
| |
|
Рис.3.4.4,г |
| |
|
Рис.3.4.4,е
| ||



 Рис.3.4.3,д
Рис.3.4.3,д

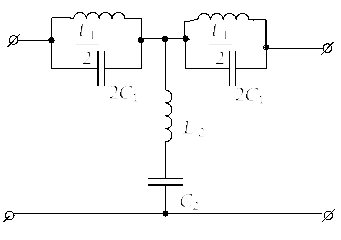 Рис.
3.4.4,а
Рис.
3.4.4,а Рис.3.4.4,б
Рис.3.4.4,б



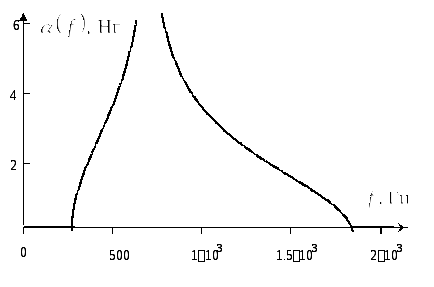 Рис.3.4.4,д
Рис.3.4.4,д
