Тема 8. Кривые второго порядка

8.1. Типовые примеры

Пример 8.1.1. Эксцентриситет линии второго порядка равен

5

, а рас-

3

стояние между фокусами равно 2

5. Определить вид линии и найти ее канони-

ческое уравнение.

Решение. По величине эксцентриситета ε=

5

<

1 определяет, что линия

3

второго порядка – эллипс. Из условия задачи имеем 2c = 2

5 c =

5.

Найдем полуоси эллипса. Так как

ε =

c

, c =

5, то

5

=

5

a =3.

a

3

a

Из соотношения c2 = a2 − b2

находим

b2 = a2 −c2 b = 9 −5 = 2.

Таким образом, каноническое уравнение эллипса имеет вид

x2

+

y2

=1.

9

4

Пример 8.1.2. Определить линию, провести ее полное исследование, по-

строить график а) 3x2 − 2 y2 = 6,

б) y2 = −6x.

Решение.

а) преобразуем уравнение к каноническому виду

3x2 − 2 y2 = 6

3x2

− 2 y2 =1

x2

−

y2

=1.

6

6

2

3

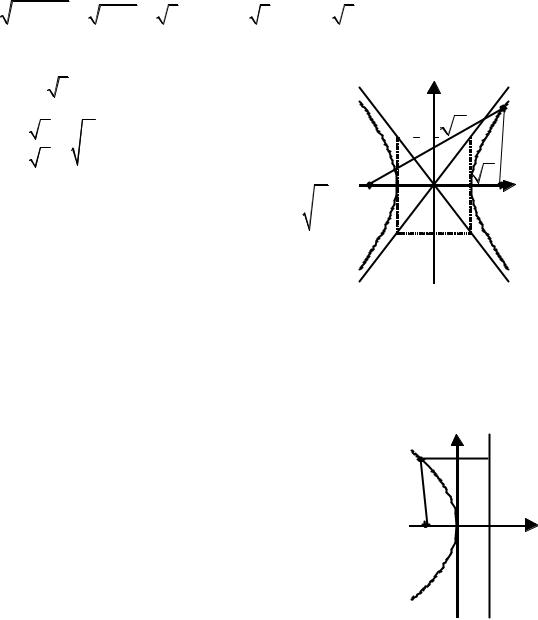
По каноническому уравнению определяем, что линия – гипербола, у ко-

торой действительная ось – Ox , мнимая ось – Oy .

Исследование:

1) a =

3, b =

2 – действительная и мнимая полуоси,

A1 (−

3,0),

A2 ( 3,0) – вершины;

34

2)

c =

a

2 + b2

=

3 + 2 =

5 F (− 5,0),

F (

5,0)

– фокусы гипербо-

1

2

лы;

3)

r1 − r2

= 2

3;

y

M

4)

ε =

c

=

5

=

5

>1;

r1

2

a

3

3

A2

3

5) асимптоты – это прямые

b

2

F

A

О a

F x

y = ± a x y = ±

3 x.

1

1

2

Построим кривую (рис. 8.1.1)

-b

рис. 8.1.1

б) по каноническому уравнению y2 = −6x определяем, что кривая – пара-

бола с параметром p = −3.

Исследование:

y

1)

O(0,0)

– вершина параболы;

M

d

3

3

r

2)

– фокус, x =

– директриса;

F −

2

.0

2

F

O

3

x

3)

r = d, где r

– расстояние от этой точки до директри-

−3

2

2

сы;

4)

ε =1.

РИС. 8.1.2

Построим график параболы (РИС. 8.1.2)

1)

x2

+

y2

=1,

2) x2 −3y2 =9,

4

9

3) y2 =8x,

4) x2 + y2 =16,

5) 9x2 + 4 y2 =9,

6) 9 y2 − 4x2 =36,

7) y2 = −10x,

8) 3y = −x2 ,

9) x2 −3y2 =1,

10) 2x2 − y2 = 0 .

8.3.2. Найти каноническое уравнение эллипса, зная его вершину A2 (6,0)

в точ-

ку M (3,

3) на эллипсе.

8.3.3. Эксцентриситет линии второго порядка равен

4 , а расстояние между фо-

3

кусами 24. Определить линии и найти ее каноническое уравнение.

8.3.4. Линия второго порядка имеет эксцентриситет

2

и вершину A (3

2, 0).

2

2