
Matematika_och_poln_2_semestr_Ekzamen
.pdf
-: 
+:
I:
S: Общий интеграл дифференциального уравнения 1-го порядка имеет вид:
|
. Тогда при начальном условии |
частный |
|
интеграл этого уравнения имеет вид … |
|
|
|
+: |
|
|
|
-: |
|
|
|
-: |
|
|
|
-: |
|
|
|
I: |
|
|
|
S: Решение задачи Коши |
, |
имеет вид… |
|
-: |
|
|
|
-: |
|
|
|
+: |
|
|
|
-: |
|
|
|
I: |
|
|
|
S: Если задача Коши для |
дифференциального |
уравнения |
имеет вид |
||
, |
, |
то |
в |
общем |
решении |
произвольная постоянная С равна … |
|
|
|||
+: 15 |
|
|
|
|
|
41
I:
S: Если задача Коши для дифференциального уравнения имеет вид
 ,
,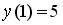 , то в общем решении
, то в общем решении 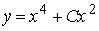 произвольная постоянная С равна …
произвольная постоянная С равна …
+: 4
I:
S: Если задача Коши для дифференциального уравнения имеет вид
 ,
,  , то в общем решении
, то в общем решении  при произвольная постоянная С равна …
при произвольная постоянная С равна …
+: -3
I:
S: Если задача Коши для дифференциального уравнения имеет вид
 ,
,  , то в общем решении
, то в общем решении  произвольная постоянная С равна …
произвольная постоянная С равна …
+: -7
I:
S: Если задача Коши для дифференциального уравнения имеет вид
 ,
,  , то в общем решении
, то в общем решении  произвольная постоянная С равна …
произвольная постоянная С равна …
+: 3
V2: Линейные дифференциальные уравнения высших порядков
I:
S: Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …
+:  ,
, 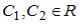 -:
-:  ,
,  -:
-:  ,
,  -:
-: 
I:
S: Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …
-:  ,
, 
42
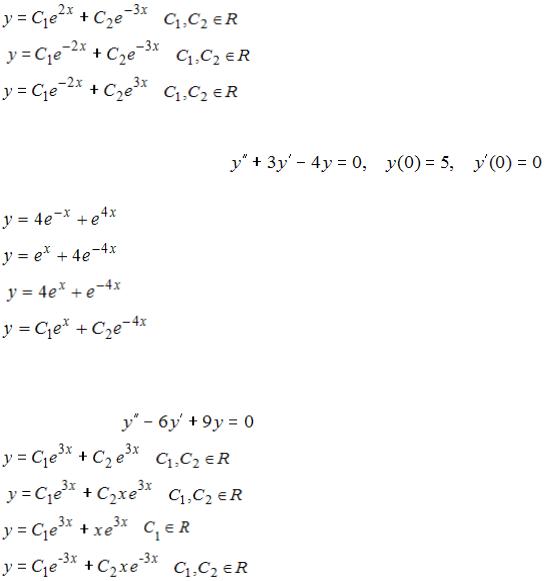
-: |
, |
|
+: |
, |
|
-: |
, |
|
I: |
|
|
S: Решение |
задачи Коши |
имеет |
вид… |
|
|
-: |
|
|
-: |
|
|
+: |
|
|
-: |
|
|
I:
S: Общее решение линейного однородного дифференциального уравнения
второго порядка |
имеет вид … |
-: |
, |
+: |
, |
-: |
, |
-: |
, |
I:
S: Функция  является общим решением линейного однородного дифференциального уравнения. Тогда его характеристическое уравнение имеет вид …
является общим решением линейного однородного дифференциального уравнения. Тогда его характеристическое уравнение имеет вид …
-: 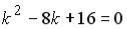 +:
+: 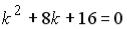 -:
-:  -:
-: 
I:
43
S:Однородному дифференциальному уравнению второго порядка
 соответствует характеристическое уравнение …
соответствует характеристическое уравнение …
-:  +:
+: 
-:  -:
-: 
I:
S: Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
L1:  L2:
L2: 
L3: 
R1:  R2:
R2:  R3:
R3: 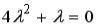
R4:  R5:
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
L1: 
L2: 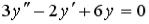 L3:
L3: 
R1:  R2:
R2:  R3:
R3: 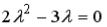
R4:  R5:
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
L1: 
44
L2: 
L3: 
R1: 
R2: 
R3: 
R4: 
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
L1:  L2:
L2:  L3:
L3: 
R1: 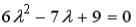
R2:  R3:
R3:  R4:
R4:  R5:
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и его характеристическим уравнением:
L1:  L2:
L2: 
L3: 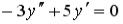
R1:  R2:
R2:  R3:
R3:  R4:
R4: 
R5: 
45

I:
S: Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …
-:  ,
,  +:
+:  ,
, 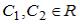 -:
-:  ,
,  -:
-: 
I:
S: Общее решение линейного однородного дифференциального уравнения второго порядка  имеет вид …
имеет вид …
+: 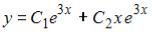 ,
,  -:
-:  ,
,  -:
-:  ,
, 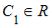 -:
-:  ,
, 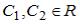
I:
S:Общим видом частного решения дифференциального уравнения
является …
-: +: -: -:
I:
S:Общим видом частного решения дифференциального уравнения
является …
-:
-:
+:
-:
46

I:
S:Общим видом частного решения дифференциального уравнения
является …
-:
-:
+: -:
-: 
I:
S: Установите соответствие между дифференциальным уравнением и общим видом его частного решения
L1:  L2:
L2: 
L3: 
R1: 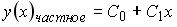 R2:
R2:  R3:
R3:  R4:
R4: 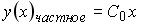
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и общим видом его частного решения
L1:  L2:
L2: 
L3: 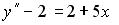
R1: 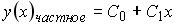 R2:
R2:  R3:
R3:  R4:
R4:  R5:
R5: 
47
I:
S: Установите соответствие между дифференциальным уравнением и общим видом его частного решения
L1:  L2:
L2: 
L3: 
R1:  R2:
R2: 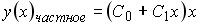 R3:
R3:  R4:
R4:  R5:
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и общим видом его частного решения
L1:  L2:
L2: 
L3: 
R1:  R2:
R2: 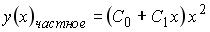 R3:
R3:  R4:
R4:  R5:
R5: 
I:
S: Установите соответствие между дифференциальным уравнением и общим видом его частного решения
L1:  L2:
L2: 
L3: 
R1:  R2:
R2: 
48

R3: 
R4: 
I:
S: Общее решение линейного неоднородного дифференциального уравнения
2-го порядка 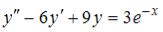 имеет вид …
имеет вид …
-:  +:
+: 
-:  -:
-: 
V2: Дифференциальные уравнения высших порядков, допускающие понижение порядка
I:
S:После понижения порядка дифференциальное уравнение
приводится к виду …
-: 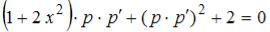 +:
+: 
-:
-:
I:
S: Общее решение дифференциального уравнения 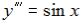 имеет вид …
имеет вид …
-: |
, |
-: |
, |
-: |
, |
49

+: |
, |
I: |
|
S: Решение задачи Коши |
имеет вид … |
-: |
|
-: |
|
-: |
|
+: |
|
I:
S: Дифференциальное уравнение y f (x, y ) допускает понижение порядка
с помощью замены:
-: y ux
+: y P(x), y P (x) -: y P( y), y P dPdy -: y P(x), y P dPdx
I:
S: Порядок дифференциального уравнения  можно понизить заменой …
можно понизить заменой …
+:  -:
-:  -:
-:  -:
-: 
I:
S: Общее решение дифференциального уравнения  имеет вид …
имеет вид …
-:  -:
-: 
-:  +:
+: 
50
