Matematika_och_poln_2_semestr_Ekzamen
.pdf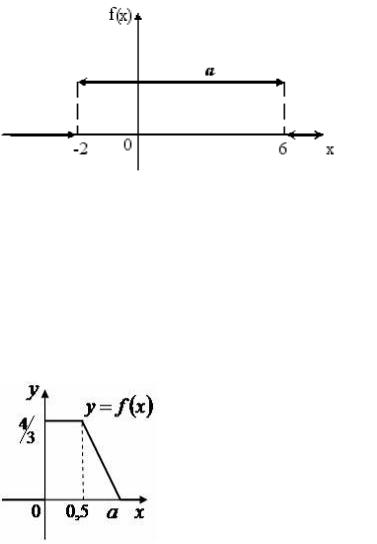
S: График плотности распределения вероятностей непрерывной случайной величины Х, распределѐнной равномерно в интервале 
, имеет вид:
Тогда значение a равно…
+: 1/8 -: 1/6 -: 1 -: 1/4
I:
S: График плотности распределения вероятностей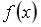 
случайной величины приведен на рисунке.
Тогда значение a равно …
+: 1 -: 0,8
-: 
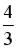
-: 0,75
I:
71
S: График плотности распределения вероятностей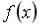 
случайной величины приведен на рисунке.
Тогда значение a равно …
-: 0,75 -: 0,7 +: 0,5 -: 0,6
I:
S: График плотности распределения вероятностей 
случайной величины приведен на рисунке.
Тогда значение a равно …
-: 1 +: 
-: 
-: 
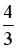72
I:
S: График плотности распределения вероятностей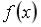 
случайной величины приведен на рисунке.
Тогда значение a равно …
+: 0,5
-: 
-: 0,75 -: 1
I:
S: График плотности распределения вероятностей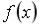 
случайной величины приведен на рисунке.
Тогда значение a равно …
-: 0,75 +: 0,5 -: 1 -: 0,8
I:
S: Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
Тогда значение С равно …
-: 4 -: 1,5 +: 2
73
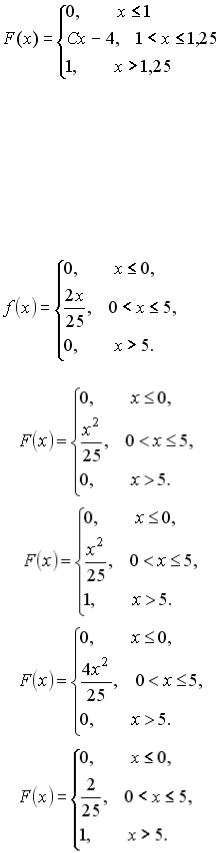
-: 2,5
I:
S: Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей
Тогда значение С равно …
-: 1,2 +: 4 -: 3
-: 2,25
I:
S: Случайная величина 
задана плотностью распределения вероятностей:
Тогда соответствующая функция распределения вероятностей равна …
-:
+:
-:
-:
74
V2: Числовые характеристики случайных величин
I:
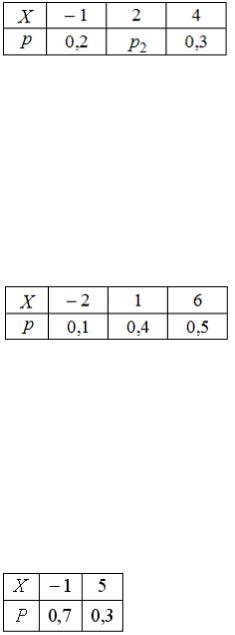
S: Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
+: 2,0
-: 
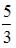
-: 4,0 -: 1,8
I:
S: Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
-: 
-: 6
-: 3,6 +: 3,2
I:
S: Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
-: 1,5 -: 2,2 -: 2 +: 0,8
I:
75
S: Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
-: 1 -: 0 -: 1,2 +: 2,3
I:
S: Дискретная случайная величина X задана законом распределения вероятностей:
Тогда ее математическое ожидание равно …
-: 4/3 -: 3,1 -: 2 +: 2,9
I:
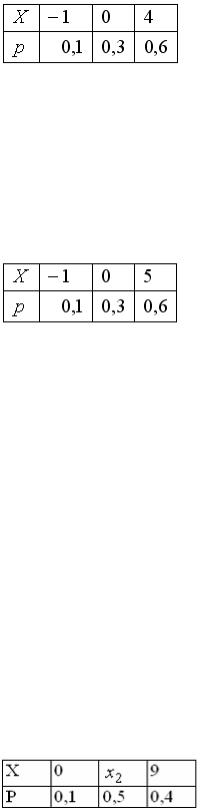
S: Дискретная случайная величина X задана законом распределения вероятностей:
Х |
–1 |
0 |
2 |
p |
0,1 |
0,3 |
0,6 |
Тогда ее математическое ожидание равно …
-: 1/3 -: 1,2 +: 1,1 -: 0,6
I:
S: Дискретная случайная величина X задана законом распределения вероятностей:
Если математическое ожидание 
, то значение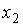 
равно …
-: 3 +: 4 -: 5 -: 6
76
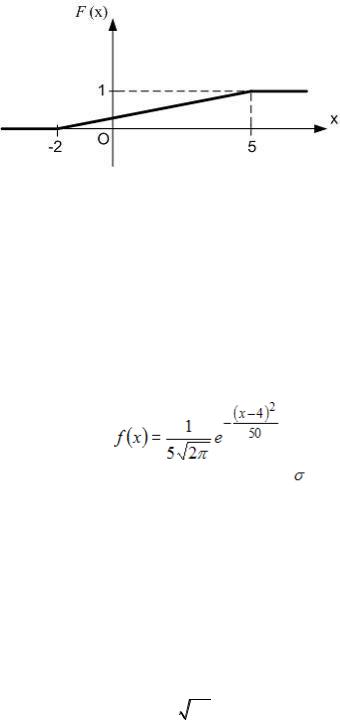
I:
S: Функция распределения вероятностей равномерно распределенной случайной величины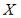 
изображена на рисунке:
Тогда ее дисперсия равна …
-: 49 -: 1,5
+: 
-: 
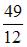I:
S: Непрерывная случайная величина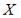 
задана плотностью распределения
вероятностей |
. |
Тогда математическое ожидание a и |
среднее квадратическое отклонение |
этой случайной величины равны … |
|
-: 
+: 
-: 
-: 
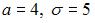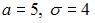I:
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 4)2 |
|
|
вероятностей f (x) |
|
e |
18 |
. Тогда математическое ожидание этой |
|||
|
|
|
|
||||
3 |
|
|
|
|
|||
2 |
|
|
|||||
случайной величины равно …
+: 4 -: 9 -: 18 -: 3
I:
77
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 4)2 |
|
|
вероятностей f (x) |
|
e |
18 |
. Тогда среднее квадратическое отклонение |
|||
|
|
|
|
||||
3 |
|
|
|
|
|||
2 |
|
|
|||||
этой случайной величины равно …
-: 4 -: 9 -: 18 +: 3
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 4)2 |
|
|
вероятностей f (x) |
|
e |
18 |
. Тогда дисперсия этой случайной |
|||
|
|
|
|
||||
3 |
|
|
|
|
|||
2 |
|
|
|||||
величины равно …
-: 4 +: 9 -: 18 -: 3
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
|
1 |
|
|
|
( x 5)2 |
|
|
вероятностей f (x) |
|
|
e |
32 . Тогда математическое ожидание этой |
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
2 |
|
||||||
4 |
|
|
|
|
|
|
||
случайной величины равно …
-: 32 +: 5 -: 16 -: 4
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
|
1 |
|
|
|
( x 5)2 |
|
|
вероятностей f (x) |
|
|
e |
32 . Тогда среднее квадратическое отклонение |
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
2 |
|
||||||
4 |
|
|
|
|
|
|
||
этой случайной величины равно …
-: 32 -: 5 -: 16 +: 4
I:
78
S: Непрерывная случайная величина X задана плотностью распределения
|
|
1 |
|
|
|
( x 5)2 |
|
|
вероятностей f (x) |
|
|
e |
32 . Тогда дисперсия этой случайной |
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
2 |
|
||||||
4 |
|
|
|
|
|
|
||
величины равно …
-: 32 -: 5 +: 16 -: 4
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 7)2 |
|
|
вероятностей f (x) |
|
e |
72 |
. Тогда математическое ожидание этой |
|||
|
|
|
|
||||
6 |
|
|
|
|
|||
2 |
|
|
|||||
случайной величины равно …
+: 7 -: 36 -: 72 -: 6
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 7)2 |
|
|
вероятностей f (x) |
|
e |
72 |
. Тогда среднее квадратическое отклонение |
|||
|
|
|
|
||||
6 |
|
|
|
|
|||
2 |
|
|
|||||
этой случайной величины равно …
-: 7 -: 36 -: 72 +: 6
I:
S: Непрерывная случайная величина X задана плотностью распределения
|
1 |
|
|
|
( x 7)2 |
|
|
вероятностей f (x) |
|
e |
72 |
. Тогда дисперсия этой случайной |
|||
|
|
|
|
||||
6 |
|
|
|
|
|||
2 |
|
|
|||||
величины равно …
-: 7 +: 36 -: 72 -: 6
I:
79
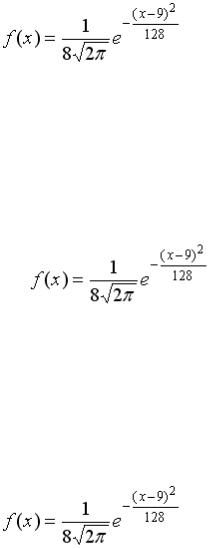
S: Непрерывная случайная величина X задана плотностью распределения
вероятностей .Тогда математическое ожидание этой случайной величины равно …
+: 9 -: 64 -: 128 -: 8
I:
S: Непрерывная случайная величина X задана плотностью распределения
вероятностей .Тогда среднее квадратическое отклонение этой случайной величины равно …
-: 9 -: 64 -: 128 +: 8
I:
S: Непрерывная случайная величина X задана плотностью распределения
вероятностей .Тогда дисперсия этой случайной величины равно …
-: 9 +: 64 -: 128 -: 8
V1: Математическая статистика
V2: Статистическое распределение выборки. Характеристики вариационного ряда
I:
S: Статистическое распределение выборки имеет вид
Хi |
–1 |
0 |
1 |
3 |
ni |
4 |
6 |
3 |
7 |
Тогда относительная частота варианты x2 = 0, равна…
-: 6 +: 0,3
80