Matematika_och_poln_2_semestr_Ekzamen
.pdfI:
S: Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 7, 9. Тогда несмещѐнная оценка математического ожидания равна…
+: 5,25 -: 5,5 -: 5 -: 6
I:
S: Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 2, 3, 6, 9. Тогда несмещѐнная оценка математического ожидания равна…
-: 5,25 -: 5,5 -: 6 +: 5
I:
S: Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
-: 1,50 -: 0,05 -: 22,90 +: 0,75
I:
S: Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
-: 12,7 -: 13,0 -: 12,8 +: 0,4
I:
S: Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
-: 18,9 -: 18,85 +: 0,46 -: 19,0
91
I:
S: Дан доверительный интервал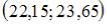 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
-: 1,50 -: 0,05 +: 22,90 -: 0,75
I:
S: Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
-: 12,7 -: 13,0 +: 12,8 -: 0,4
I:
S: Дан доверительный интервал 
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
+: 18,9 -: 18,85 -: 0,46 -: 19,0
I:
S: Точечная оценка математического ожидания нормально распределенного количественного признака равна 15. Тогда его интервальная оценка может иметь вид …
-: 
-: 
+: 
-: 
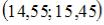I:
S: Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид …
-: (11,2; 11,8) -: (10,8; 12) +: (10,6; 13,4)
92
-: (12; 13,7)
I:
S: Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид …
-: (11,8; 12,8) +: (11,8; 14,2) -: (13; 14,7)
-: (11,6; 13)
I:
S: Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид...
+: (12,3; 13,7) -: (13; 13,7) -: (12,3; 12,8) -: (12,3; 13)
I:
S: Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид...
+: (13,8; 16,2) -: (15; 16,2) -: (13,8; 14,1) -: (13,8; 15)
I:
S: Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид...
-: (14,9; 16) +: (14,9; 17,1) -: (16; 17,1) -: (14,9; 15,2)
I:
S: Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид …
+: (8,5; 11,5) -: (8,6; 9,6) -: (10; 10,9) -: (8,4; 10)
I:
93
S: Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид …
-: (11; 12,1) -: (9,8; 10,8) +: (10,1; 11,9) -: (9,8; 11)
I:
S: Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид…
-: (11,8; 12,8) -: (11,6; 13) +: (11,8; 14,2) -: (13; 14,6)
I:
S: Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид...
+: (10,1; 11,9) -: (10,1; 11) -: (11; 11,9) -: (10,1; 10,8)
I:
S: Точечная оценка математического ожидания нормального распределения равна 13. Тогда его интервальная оценка может иметь вид...
-: (13; 13,7) -: (12,3; 12,8) +: (12,3; 13,7) -: (12,3; 13)
I:
S: Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид...
+: (13; 15)
-: (12,3; 12,8) -: (12,3; 13,7) -: (12,3; 13)
I:
S: Точечная оценка математического ожидания нормального распределения равна 17. Тогда его интервальная оценка может иметь вид...
-: (17; 17,7) +: (16,3; 17,7) -: (15,3; 17)
94
-: (12,3; 17)
I:
S: Точечная оценка математического ожидания нормального распределения равна 18. Тогда его интервальная оценка может иметь вид...
-: (17; 18)
-: (18,3; 19,8) -: (12,3; 18) +: (17,3; 18,7)
I:
S: Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид...
-: (10; 13,7) -: (9,3; 10) +: (9,1; 10,9) -: (10; 13)
I:
S: Точечная оценка математического ожидания нормального распределения равна 15. Тогда его интервальная оценка может иметь вид...
+: (14,8; 15,2) -: (15; 16,5) -: (13,8; 14,1) -: (13,8; 15)
I:
S: Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид...
-: (11,2; 11,8) -: (10,8; 12) +: (11,6; 12,4) -: (12; 13,7)
I:
S: Точечная оценка математического ожидания нормального распределения равна 16. Тогда его интервальная оценка может иметь вид...
-: (14,9; 16) +: (15,9; 16,1) -: (16; 17,9) -: (14,9; 15,5)
I:
95
S: Точечная оценка математического ожидания нормального распределения равна 17. Тогда его интервальная оценка может иметь вид...
-: (17; 17,9) +: (16,4; 17,6) -: (15,3; 17) -: (12,3; 17)
I:
S: Точечная оценка математического ожидания нормального распределения равна 18. Тогда его интервальная оценка может иметь вид...
-: (17; 18)
-: (18,3; 19,8) -: (11,3; 18) +: (17,5; 18,5)
I:
S: Точечная оценка математического ожидания нормального распределения равна 14. Тогда его интервальная оценка может иметь вид...
+: (13,2; 14,8) -: (14; 19,8) -: (14; 15,7) -: (12,3; 14)
I:
S: Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид...
-: (11,2; 11,8) -: (11,8; 12) +: (11,6; 12,4) -: (12; 14,7)
I:
S: Точечная оценка математического ожидания нормального распределения равна 10. Тогда его интервальная оценка может иметь вид...
-: (10; 14,7) -: (8,3; 10) +: (9,1; 10,9) -: (10; 12)
I:
S: Точечная оценка математического ожидания нормального распределения равна 11. Тогда его интервальная оценка может иметь вид...
+: (10,1; 11,9) -: (10,9; 11) -: (11; 11,1)
96
-: (10,1; 10,8)
V2: Проверка статистических гипотез
I:
S: Основная гипотеза имеет вид 
. Тогда конкурирующей может являться гипотеза …
-: 
-: 
-: 
+: 
I:
S: Левосторонняя критическая область может определяться из соотношения
…
-: 
-: 
+: 
-: 
I:
S: Основная гипотеза имеет вид 
. Тогда конкурирующей может являться гипотеза …
-: 
-: 
+: 
-: 
I:
S: Соотношением вида 
можно определить … -: левостороннюю критическую область -: область принятия гипотезы -: двустороннюю критическую область
+: правостороннюю критическую область
97