
- •Изучение вращательного движения твердого тела
- •Теория метода
- •Вращение твердого тела вокруг неподвижной точки
- •Вращение твердого тела вокруг неподвижной оси
- •Законы динамики вращательного движения
- •Описание экспериментальной установки
- •Выполнение работы
- •Контрольные вопросы
- •Литература
- •Изучение законов свободных механических колебаний
- •Теория метода
- •Описание экспериментальной установки
- •Выполнение работы
- •Контрольные вопросы
- •Литература
- •Изучение ускорения свободно падающих тел
- •Теория метода
- •Описание экспериментальной установки
- •Определение ускорения свободного падения
- •Контрольные вопросы
- •Литература
- •Определение ускорения свободного падения методом оборотного маятника
- •Теория метода
- •Выполнение работы
- •Контрольные вопросы
- •Литература
- •Определение модуля юнга
- •Теория метода
- •Выполнение работы
- •Контрольные вопросы
- •Литература
- •Определение модулей сдвига и кручения
- •Теория метода
- •Описание экспериментальной установки
- •Выполнение работы
- •Примечание
- •Контрольные вопросы
- •Литература
- •Определение коэффициента трения качения
- •Теория метода
- •Описание экспериментальной установки
- •Выполнение работы
- •Контрольные вопросы
- •Литература
Литература
1.Гершензон Е.М., Малов Н.Н. Курс общей физики. Механика: Учеб. пособие для студентов высш. пед. учеб. заведений. - М.: Академия, 2001. - 384с.
2. Гершензон Е.М., Мансурова А.Н. Лабораторный практикум по общей и экспериментальной физике. – М.: Академия, 2004. – 461с.
3. Савельев И.В. Курс общей физики. Т.1. Механика. Учеб. пособие. – М.: изд-во Астрель, 2005.- 336с.
4. Стрелков С.П. Механика. - М.: Лань, 2005.- 560с.
Лабораторная работа №8
Изучение законов свободных механических колебаний
Цель работы: экспериментальное изучение законов свободных колебаний физического и математического маятников.
Принадлежности: маятник универсальный ФПМ-А-01.
Теория метода
Физическим маятником называется любое твердое тело, которое под действием силы тяжести может совершать свободные колебания вокруг неподвижной горизонтальной оси. Движение маятника во времени описывается дифференциальным уравнением
![]() ,
(1)
,
(1)
где I – момент инерции маятника относительно оси колебаний; - угол отклонения маятника от положения равновесия; t – время; М – момент всех сил, действующих на маятник.
В качестве физического маятника в данной работе используется однородный стальной стержень длины L (цилиндрической формы), не содержащий дополнительных грузов (чечевиц). На стержне закреплена опорная призма, острое ребро которой является осью качения маятника. Призму можно перемещать вдоль стержня, меняя таким образом расстояние а от точки опоры маятника до центра масс С (рис.1).
Момент силы тяжести, действующий на маятник, равен
![]() ,
(2)
,
(2)
где m – масса маятника.
Если пренебречь моментом сил трения, то уравнение колебаний (1) примет следующий вид:
![]() .
(3)
.
(3)
Для малых углов отклонения (sin) уравнение (3) преобразуется к виду
![]() .
(4)
.
(4)
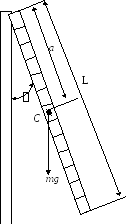
Р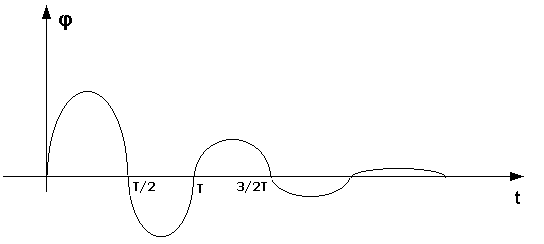 ис.1
ис.1
Рис.2
Колебания, описываемые уравнением (4),
называются гармоническими. Частным
решением (4) при начальных условиях
(t=0)=m
и
![]() является
является
![]() ,
(5)
,
(5)
где 0– круговая частота колебаний;m.- максимальный угол отклонения от положения равновесия.
Круговая частота колебаний, входящая в (5), равна
![]() .
(6)
.
(6)
Период колебаний физического маятника в этом случае равен
![]() .
(7)
.
(7)
Из (7) следует, что период колебаний не зависит от амплитуды колебаний.
При выводе уравнения (3) мы не учитывали возможного затухания колебаний маятника вследствие действия силы трения. Проанализируем влияние силы трения для малых амплитуд колебаний. Учитывая пропорциональность момента сил трения угловой скорости маятника, выражение (4) примет вид:
![]() ,
(8)
,
(8)
где - коэффициент затухания.
В этом случае решение (8) при тех же начальных условиях запишется
![]() .
(9)
.
(9)
Из (9) следует, что колебания в этом случае происходят с экспоненциальным затуханием амплитуды. Период затухающих колебаний равен
![]() .
(10)
.
(10)
График затухающих колебаний представлен на рис.2.
Натуральный логарифм отношения двух последующих амплитуд, отстающих друг от друга на время, равное периоду, называется логарифмическим декрементом затухания.
 .
(11)
.
(11)
Во многих случаях затухание колебаний невелико (<<o) и почти не сказывается на частоте колебаний. В этих случаях можно считать, чтоТТо.
Идеальной колеблющейся системой является математический маятник – материальная точка, подвешенная на нерастяжимой и невесомой нити (рис.3). В реальности данный маятник неосуществим, но его хорошим приближением является шарик, подвешенный на длинной нерастяжимой нити (если размеры шарика на много меньше длины нити, а масса шарика во много раз больше массы нити).
В этом случаеI=m.(l’)2;а=(l’). Тогда
(7) примет вид:
этом случаеI=m.(l’)2;а=(l’). Тогда
(7) примет вид:
![]() .
(12)
.
(12)
То есть период колебаний математического маятника зависит только лишь от его длины.
Сравнивая формулы (12) и (7) видим, что физический маятник колеблется также, как математический маятник с длиной
![]() .
Длину математического маятникаl’,
который колеблется с частотой колебаний
некоторого физического маятника называют
приведенной длиной физического маятника.
.
Длину математического маятникаl’,
который колеблется с частотой колебаний
некоторого физического маятника называют
приведенной длиной физического маятника.
