Литература

1. Гершензон Е.М., Мансурова А.Н. Лабораторный практикум по общей и экспериментальной физике. – М.: Академия, 2004. – 461с.

2. Савельев И.В. Курс общей физики. Т.1. Механика. Учеб. пособие. – М.: изд-во Астрель, 2005.- 336с.

3. Сивухин Д.В. Общий курс физики. Т.1. Механика. – М.: Академия, 2002.- 519с.

Лабоpaторная работа № 11

Определение модуля юнга

Цель работы: экспериментальное определение модуля Юнга материала проволоки методом растяжения.

Принадлежности: специальная установка, набор гирь, индикатор удлинения.

Теория метода

Под действием внешних сил твердое тело изменяет форму и объем - деформируется. При деформациях твердого тела, например металла, в нем происходят очень сложные явления, которые еще недостаточно исследованы.

Металлы представляют совокупность хаотически расположенных и различно ориентированных относительно друг друга мелких кристалликов. Вследствие этого упругие свойства металла по различным направлениям одинаковы и металл является изотропным телом. Деформацию в металле грубо можно представить так: в зоне упругих деформаций (упругая деформация - это такая деформация, когда тело после прекращения действия сил, вызывающих деформацию принимает первоначальные размеры и форму) кристаллики металла изменяют свою форму не сдвигаясь и не разрушаясь. После снятия нагрузки они возвращаются в прежнее состояние под влиянием сил взаимодействий между кристалликами. Таким образом, в упруго-деформированном теле возникают внутренние силы, которые уравновешивают внешние силы, приложенные к телу. Физическая величина , равная отношению упругой силы F_упр к площади сечения S тела, называется напряжением:

. (1)

Напряжение называется нормальным, если F_упр направлена по нормали к площади S и касательным, если она направлена по касательной к площадке. Для нормального напряжения

. (2)

В зоне пластических деформаций (пластические деформации возникают тогда, когда силы, действующие на тело, перешли определенный предел, называемый пределом упругости, определенный для каждого тела; после превышения внешними силами этого предела, тело не восстанавливает свою форму и размеры) происходит, кроме изменения формы кристалликов, еще и скольжение в них, а также смещение их относительно друг друга и разламывание. Эти изменения уже не могут исчезнуть после снятия нагрузки. Тело остается деформированным, в нем возникают остаточные деформации. Если после появления в теле остаточных деформаций мы продолжаем увеличивать внешнюю силу, то наблюдается разрушение тела. Это явление наступает тогда, когда напряжение, возникающее в теле под действием деформирующей силы, переходит предел прочности тела. Деформации тела бывают разные: растяжение, сжатие, сдвиг, кручение, изгиб. Мерой деформации является относительная деформация , равная отношению абсолютной деформациик первоначальному значению величины, характеризующей размеры или форму тела. При всестороннем растяжении или сжатииозначает объем V (увеличение или уменьшение объемаV, называемое деформацией), а при продольном растяжении или сжатии означает длинуl. Зависимость между напряжением и относительной деформацией показана на рис .1. Точка А соответствует пределу упругости, ордината АД - величина напряжения, выражает предел упругости, ордината ВС - предел прочности. Английский физик Г.Гук установил закон упругих деформаций, который утверждает, что напряжение упруго деформированного тела пропорционально его относительной деформации:

, (3)

г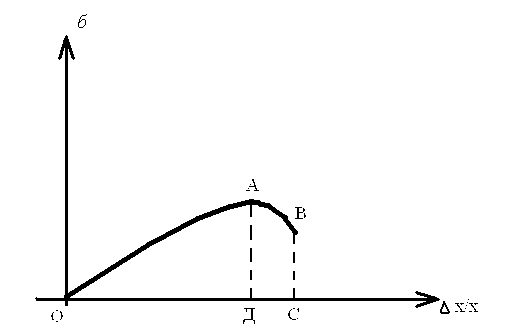деk - модуль упругости.

Рис.1

Закон Гука справедлив только на участке ОА ( рис .1). При продольном растя-жении или сжатии модуль упругости называется модулем Юнга и закон Гука запишется так:

, (4)

где Е - модуль Юнга.

Учтя, что , получим что при модуль Юнга Е=_о=F/S, т.е. модуль Юнга равен нормальнoму напряжению, которое возникло бы в образце при уве­личения его длины в два раза, если бы при этих деформациях был справедлив закон Гука.

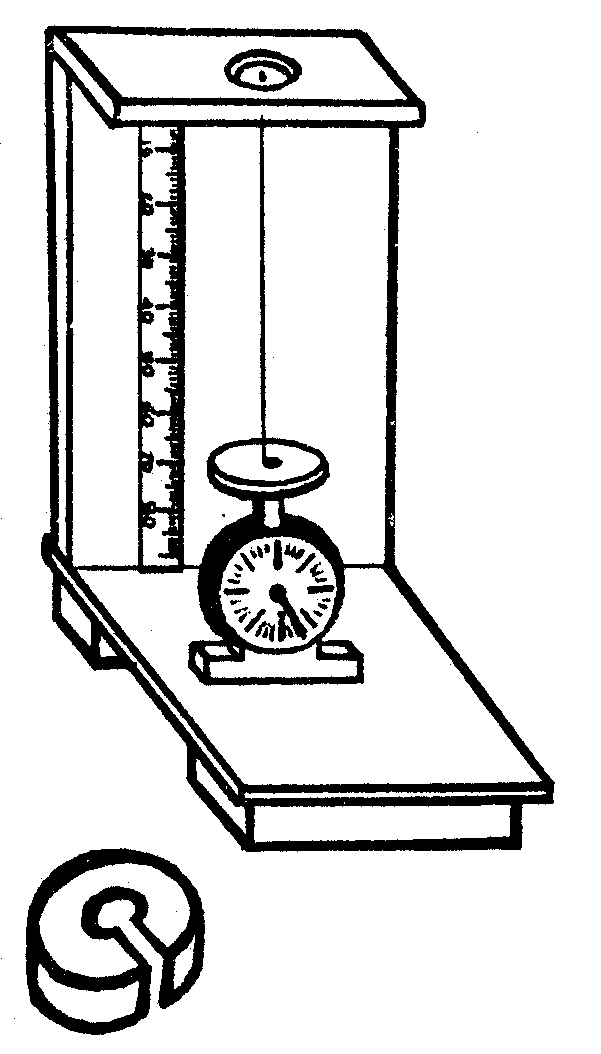
Рис.2

Так как относительная деформация  - отвлеченное число, то единица модуля упругости в системе Си: . При растяжении тело одновременно испытывает уменьшение поперечныx размеров  на величину . Деформация поперечного сжатия связана с деформацией продольного растяжения. Отношение коэффициента относительного уменьшения сечения к коэффициенту относительного удлинения называется коэффициентом Пуассона

. (5)

Описание экспериментальной установки.

Определить модуль упругости можно методом растяжения проволоки, закрепленной неподвижно с одного и нагруженной с другого конца грузом определенного веса. Действие этой силы вызывает деформацию растяжения. Установка для определения модуля Юнга (рис.2) состоит из подставки, на основании которой укреплен микрометр со столиком 3. В верхней части подставки имеется винт для зажима проволоки 2. На одном конце проволоки имеется кольцо для соединений со столиком микрометра. Свободный конец проволоки пропускается через отверстие зажима, натягивается и крепится винтом 2. Устанавливают шкалу микрометра 1 на 0 и нагружают столик грузами с известной массой. Стрелка микрометрa откланяется вследствие деформации проволоки под действием веса грузов, и показывает величину удлинения проволоки l.